大电网中虚拟同步发电机惯量支撑与一次调频功能定位辨析

秦晓辉, 苏丽宁, 迟永宁, 郭 强, 徐希望

(1. 中国电力科学研究院有限公司, 北京市 100192;2. 电网安全与节能国家重点实验室(中国电力科学研究院有限公司), 北京市 100192)

0 引言

为满足资源、环境的可持续发展需求,近年来中国大力发展新能源发电,风电、光伏装机容量持续快速增长,部分地区电网新能源出力占比已超过50%[1-3]。风电、光伏并网逆变器本身属于不具备转动惯量的静止元件,无法像同步机一样自发响应频率变化。并且为了最大化利用能源,新能源机组通常采用追踪最大功率的控制方式,不提供有功备用,因此不具备类似同步机在系统频率变化时的一次调频能力。随着新能源渗透率和直流受电比例的不断提高,同步电网的惯量和一次调频的能力不断下降,给系统在大功率缺额冲击下的频率稳定性与恢复能力带来了风险[3-10]。频率问题在受端电网中表现尤为突出,2015年某馈入华东的特高压直流发生双极闭锁,瞬时损失功率5 400 MW,导致系统频率最低跌至49.56 Hz,为近10年来首次跌破49.8 Hz,频率越限时间长达数百秒[3],给新形势下的大电网频率安全问题敲响了警钟。

为应对上述风险,通过在新能源并网控制器中引入模拟同步机转子运动方程和一次调频等环节的设计,使新能源机组具有同步发电机组的惯量、阻尼、调频和调压等并网运行外特性,从而提高新能源高比例接入电网的运行适应性和安全稳定水平。此类控制方法可以统称为“虚拟同步发电机(virtual synchronous generator,VSG)”控制[11-16]。

国家电网公司正在大力推进VSG在大电网中的应用,将在张北风光储输基地建设世界上容量最大的VSG示范工程,现阶段主要关注一次调频与惯量支撑这两大功能;但目前针对VSG惯量支撑和一次调频的研究多关注其本身的控制策略和响应特性以及在微网和局部电网中的应用[17-28],尚无相关文献在接入大电网场景下对VSG的惯量支撑和一次调频对电网频率的作用开展深入研究,而且从目前相关标准的制定过程来看,学术界和工业界对VSG惯量支撑与一次调频这两者功能定位的认识及其在大电网具体应用中的理解也尚存在一些不一致和不清晰之处,亟须开展有针对性的深入分析研究。

针对以上问题,本文首先深入分析了VSG的惯量支撑功能及其物理意义,推导了VSG的惯量支撑功率表达式;然后,分析了VSG一次调频的功能要求和物理意义,详细辨析了VSG惯量支撑功能与一次调频功能的定位区分;随后,建立了VSG惯量支撑与一次调频功能的机电暂态仿真模型,并仿真分析了VSG采用不同控制功能对系统频率动态变化的作用,以及VSG在大型受端电网频率事故过程中的响应特性。最后,结合理论分析与仿真结果进一步明确了大型受端电网对VSG控制功能的需求。

1 VSG惯量支撑功能及物理意义

1.1 同步机的惯量响应

VSG的惯量支撑功能也叫惯量响应(inertia response),而本文之所以强调“支撑”,是因为通常所说的VSG的惯量响应一般只关心在系统频率变化过程中虚拟同步发电机输出的有功功率响应于系统频率变化率的功能(电流源型VSG只能模拟这一功能),但其实同步发电机全面的惯量响应包括以下两个方面。

方面1：转子的状态变量(功角、频率)在不平衡转矩下的响应

电网的频率变化往往由系统的功率不平衡(输入、输出功率不平衡)冲击引起,在此过程中,网内的各同步机都将感受到不平衡功率的作用,在不平衡功率(转矩)的作用下,各同步机状态变量的响应可由式(1)所示的转子运动方程描述。

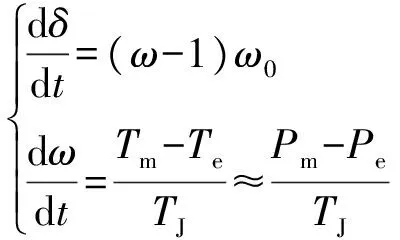
(1)

式中:t为时间;ω0为系统额定电角速度;TJ为转子惯性时间常数;δ为转子功角;ω为转子电角速度;Tm,Te,Pm,Pe分别为转子的机械转矩、电磁转矩、机械功率和电磁功率。式中各量除t,ω0,TJ为有名值外,其余均为标幺值。

方面2：发电机转子动能与输出电磁功率在系统频率变化时的响应

在系统频率发生变化时,网内各发电机的转子速度基本同步变化,在此过程中,发电机转子的动能也在相应发生变化,在假设施加到转子上的机械输入功率保持不变时,转子动能的变化量将以发电机电磁功率的形式注入电网中,此功率即为惯量支撑功率。

下面重点推导惯量支撑功率的表达式。

1.2 同步机的惯量支撑功率表达式

系统在额定频率正常运行时,同步机转子以额定转速ΩN(即同步转速)转动的动能Wk为:

(2)

式中:J为转子转动惯量，单位为kg·m2;ΩN为转子的额定机械角速度。

根据发电机转子惯性时间常数TJ的物理意义[29],TJ为在转子上施加额定转矩Tm后,转子从停顿状态(机械角速度Ω=0)加速到额定状态(机械角速度Ω=ΩN)时所经过的时间,即有

(3)

式中:PN为同步机的额定功率。

根据式(3)可知,转子惯性时间常数TJ的数值为:

(4)

当发电机的极对数为1(如汽轮发电机)时,转子机械角速度Ω等于转子电角速度ω,又有

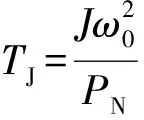
(5)

对于同步机,当转速发生变化时,其转子动能发生变化,释放或吸收的能量对外表现为输出电磁功率的增减。

设零时刻转子转速为额定转速ω0,而在时刻t,转子动能的变化量,即输出电磁功率在0～t时刻上累计的能量变化量为:

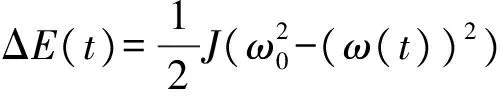
(6)

而时刻t输出的电磁功率即为该能量的微分:

(7)

式中:f(t)为系统的瞬时频率。

而由式(5)可得:

(8)

式中:f0为系统的额定频率。

将式(8)代入式(7),即得到由转子动能变化而输出的瞬时电磁功率表达式为:

(9)

因系统频率变化的相对值不会太大(绝对值超过0.8 Hz即可能引起低频减载动作,而相对值只有1.6%),所以可设f(t)≈f0,则式(9)可简化为:

(10)

式(9)和式(10)即为同步机在系统频率变化过程中由于转子动能变化而释放或吸收的电磁功率表达式,即VSG需要模拟的惯量支撑功率表达式,该式已被写入国家电网公司关于VSG技术要求与试验方法的企业标准(报批稿)。

从式(10)可以看出,同步机惯量支撑功率与系统频率的微分值(即频率变化率)的相反数成正比,因此可以看做是系统频率的微分反馈控制。

对于如图1所示的某电网频率的剧烈变化曲线,设该电网中某同步机的TJ=8 s,则按照式(9)得到该机输出的惯量支撑功率(以本机额定功率标幺化)曲线如图2所示。

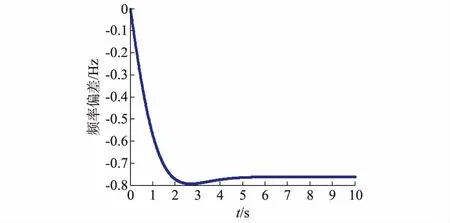
图1 电网频率变化曲线Fig.1 Frequency changing curve of power system

图2 惯量支撑功率曲线Fig.2 Inertia support power curve

从图2中可以看出,当电网频率快速跌落的初始瞬间,惯量支撑功率最大,对于如图1所示的频率剧烈变化,惯量支撑功率最大可达该机额定功率的13%左右。当电网频率达到最低点以后逐渐回升至平稳的过程中,惯量支撑功率分别为负数(频率回升期间)和0(频率平稳后)。

值得说明的是,如果为了设备安全考虑,不想让惯量支撑功率瞬间跃升,可以在式(10)的基础上加一阶惯性环节进行缓冲调节,详见下文4.1节与4.2节。一阶惯性环节时间常数的取值须与虚拟惯性时间常数相协调,并可在给定系统频率曲线输入的情况下通过时域仿真调校缓冲效果。

1.3 同步机惯量支撑功能的物理意义

如1.1节所述,同步机的惯量支撑功能实际上包括以下两个方面。

方面1:转子的状态变量(功角、频率)在不平衡转矩下的响应

同步机转子的功角和频率是不可突变的机械状态量,该状态量将在转子不平衡转矩的作用下,按照式(1)所示的微分方程发生变化,该响应的物理意义是质块在外力作用下运动状态的改变。

值得指出的是,该响应隐含的意义是同步机内电势的相位不会发生突变(内电势幅值由转子磁链制约也不会突变),也就是说同步机的内电势是相位和幅值都不会突变的独立电压源,同步机的“电压支撑”作用也由此而来。因此,只有真实同步机和电压源型VSG才有此项响应功能。

方面2:发电机转子动能与输出电磁功率在系统频率变化时的响应

如前所述,此项即为同步机的惯量支撑功率,它的物理意义是:质块在运动状态发生变化时对外释放或吸收的能量。

可以看出,方面1和2虽然描述的是同一个运动过程,但是差异却是很明显的,首先是侧重点和因果关系不同:方面1侧重于描述外力作用下质块的运动规律,方面2侧重于描述运动过程中质块由于运动状态不同而引起的能量变化,所以方面1是策动的因,方面2是响应的果。其次,同步机输出电磁功率根本上仍由方面1决定,而不由方面2决定。这是因为对于同步机来说,外部网络发生扰动瞬间该机的电磁功率突变量由扰动点与该机之间的电气距离决定,而扰动后机电振荡过程中该机电磁功率则由该机与外部网络中其他同步机之间的相对功角差和网络参数决定。也就是说,扰动后机电摇摆过程中该机与网络中其他同步机之间的相对运动决定了该机的输出电磁功率,该相对运动可由方面1描述;而该机输出电磁功率的变化又引起转子动能的变化,数值上则可由方面2描述,但须注意到本质上并不是转子动能的变化引起了输出电磁功率的变化,而是正好相反。所以仅模拟方面2的响应并不能真正全面地反映真实的同步机惯量支撑功能。

还值得指出的是,对于真实同步机和电压源型VSG,因其内电势为电压源,而它的输出电流和电磁功率是自由的非目标受控量,由外部网络决定,所以同步机的惯量支撑功率可以瞬间释放出来,是电压源在外界功率不平衡时被动应激的自发即时响应。而对于电流源型的VSG,因其输出电流和电磁功率均为目标控制量,则需要按照式(9)或式(10)形成附加功率控制指令,才能主动尽可能地模拟这一惯量支撑功率。

2 VSG一次调频功能及物理意义

2.1 VSG的一次调频功能要求

当系统频率偏差值大于±0.03 Hz(一次调频死区范围),VSG的有功出力大于20%PN时,VSG应能根据频率偏差调节有功输出,参与电网一次调频。

VSG参与一次调频的具体要求如下。

1)当系统频率下降时,VSG应增加有功输出,有功出力可增加量的最大值至少为10%PN。

2)当系统频率上升时,VSG应减少有功输出,有功出力可减少量的最大值至少为20%PN,降出力至20%PN时,VSG输出有功功率可不再向下调节。

3)考虑到与传统机组的协调性,VSG的有功调频系数Kf(定义见附录A)推荐为10～20,VSG参与电网一次调频曲线见附录B。

4)虽然VSG的调节速度可以更快,但是考虑到与传统机组的协调性[30],因此仍应推荐VSG与传统机组一次调频性能的主要指标基本保持一致为宜,即一次调频的启动时间(达到10%目标负荷的时间)应不大于3 s,达到90%目标负荷的响应时间应不大于12 s,达到95%目标负荷的调节时间应不大于30 s。

一次调频功率与系统频率的偏差值的相反数成正比,因此可看作是系统频率的比例反馈控制。

2.2 VSG一次调频的物理意义

VSG的一次调频功能本质上是VSG的有功—频率下垂控制,以实现VSG有功输出随电网系统频率变化的自适应调节,为使电网达到新的功率平衡点而做出相应的贡献。

值得指出的是,电网的系统频率是反映交流电网全局功率盈缺的一个重要运行指标,当电网中功率保持平衡时,系统频率保持不变;当电网中发生功率缺额(如发电机掉机)时,系统频率下降;当电网中发生功率盈余(如大用户负荷突然退出)时,系统频率上升。

对于电压源型VSG,因为其输出的电磁功率不是目标受控量,所以和真实同步机一样,一次调频靠改变原动机的输入功率指令来实现一次调频。而对于电流源型VSG,因为其输出电流和电磁功率是直接的目标受控量,所以可通过在电磁功率指令上直接叠加一次调频功率指令来实现一次调频,速度可以做到更快。

3 VSG惯量支撑与一次调频的功能定位区分辨析

如前所述,VSG的惯量支撑功能与一次调频功能是两种不同的控制功能,下面对两者各自的功能定位进行详细的区分辨析。

1)从控制规律的特点来看:惯量支撑是对系统频率的微分反馈控制,而一次调频是对系统频率的比例反馈控制。相对于一次调频控制,惯量支撑控制因其微分控制规律,具有超前特性,可以很快响应;而在系统频率变化初期的频率偏差较小,一次调频控制因其比例控制规律,所以一次调频功率出力也较小,显得相对较慢。但值得指出的是,这两种控制都无法实现对系统频率的无差调节,而只有二次调频控制(具有积分反馈控制特性)才能实现对系统频率的无差调节。

2)从能量变化角度来看:惯量支撑只是一个非常短时的冲击型功率支撑,当系统频率不再变化(频率偏差仍然存在)时,支撑功率为0,该支撑功率所产生的累积能量非常有限;而一次调频功率是一个持续的功率支援,只要系统频率偏差存在,一次调频功率就一直存在,该功率所产生的累积能量非常可观,从而可以使系统频率停止下跌(上升),稳定在一个较低(较高)的平衡点继续运行。

3)从功能定位及作用来看:以功率缺额事件导致系统频率跌落为例,惯量支撑的功能定位和主要作用是延缓系统的频率变化率,阻止系统频率快速下跌,从而为一次调频赢得时间,但并不能有效抑制频率的跌落深度;而一次调频的功能定位和主要作用是提供可以响应系统频率偏差的持续的有功功率支援,以阻止系统频率的持续跌落,使其可以达到新的平衡,维持在较低的频率水平继续运行。

还值得指出的是,对于电流源型VSG,因其内电势不是独立电压源,所以无法对系统频率产生直接的影响(独立电压源的电角频率才可以对电网系统频率产生直接的影响和约束),而是通过输出的惯量支撑功率和一次调频功率间接减轻网内其他同步机的电磁功率负担,从而减缓其他同步机转子转速的变化率和变化幅度,以达到间接为系统频率提供帮助的目的。

4 VSG在大电网频率事故过程中对系统频率的作用及其响应特性仿真分析

4.1VSG惯量支撑功能与一次调频功能的机电暂态建模

如第1节所述,VSG的惯量支撑功能的严格数学表达式如式(9)—式(10)所示,但是从图2中可知,对于8 s的虚拟惯性时间常数,在系统频率急剧跌落的瞬间,惯量支撑功率的瞬间输出可能达到额定功率的百分之十几,这个瞬间不平衡转矩可能会对风机设备相关部件产生较大的转矩冲击,从而不利于风机的安全稳定运行,所以,在设计风机的惯量支撑控制功能时,一般会在式(10)后面再加上一个时间常数为T(可调)的一阶惯性环节进行缓冲[31],传递函数如图3所示。

图3 风机VSG惯量支撑控制传递函数
Fig.3 Transfer function of inertia support control of VSG for wind turbines

一次调频功能的建模则相对简单,但值得说明的是,如果不考虑配置储能,那么风机具备一次调频能力的前提是运行出力留有备用。而风机通常运行在最大功率点跟踪(MPPT)模式下,即不留备用;而只有在高风速时,为防止风机转速突破机组最大转速上限,才不得不收桨进入恒功率运行区间,此时可认为天然地留有出力备用;否则在低、中风速对应的风机MPPT运行区间和恒转速运行区间,则必须通过主动收桨来牺牲最大功率追踪能力,才可获得出力备用,否则没有备用。

4.2大电网功率缺额事故中VSG不同控制功能对系统频率变化的作用及响应特性仿真分析

在PSASP中建立VSG惯量支撑功能和一次调频功能的机电暂态仿真模型,以某大型受端电网作为仿真算例,该大区电网在某方式下开机约208 GW,考虑在大区电网内系统频率变化率较低,为了观察到VSG较为显著的惯量支撑功率,取较大的虚拟惯性时间常数TJ为55 s,同时取一阶惯性环节时间常数为5.5 s;一次调频系数Kf取为10。

在该大区电网内全为真实同步机和含有12 000 MW双馈风机两种情况下,设置故障为某特高压直流发生双极闭锁,损失8 000 MW外来电力,功率缺额比例约为3.85%,仿真得到两种情况下系统频率变化曲线如图4所示。

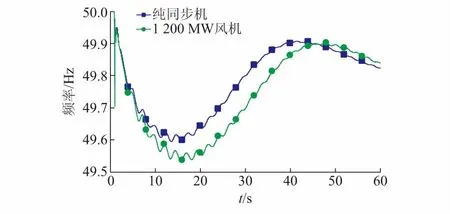
图4 大电网严重功率缺额事故中系统的频率曲线Fig.4 System frequency curves under serious active power shortage contingency in a large power grid

从图4中可以看出,在纯同步机系统情况下,受端电网的系统频率曲线的最低点为49.59 Hz;而在含12 000 MW双馈风机系统的情况下,受端电网的系统频率曲线的最低点为49.53 Hz,下降了0.06 Hz。普通双馈风机由于不具备惯量支撑与一次调频能力,从而使得系统的动态频率曲线在相同的功率缺额冲击下进一步恶化,呈现出跌落幅度更深,速度更快,持续时间更长的特征。

如果把这12 000 MW的风机进一步改造为VSG,图5给出了对于相同的功率缺额冲击,在VSG的惯量支撑功能与一次调频功能分别投入以及共同投入等不同情况下,对电网系统频率动态特性的改善作用。

图5 大电网严重功率缺额事故中VSG 不同控制功能作用下系统动态频率曲线比较Fig.5 Comparison among dynamic frequency curves corresponding to different control functions of VSG under serious active power shortage contingency in a large power grid

从图5中可以看出,纯同步机系统情况下频率动态特性最好,频率最低点最高;含12 000 MW普通双馈风机情况下系统频率动态特性最差,频率最低点最低;将此12 000 MW的风机改造为VSG,且惯量支撑控制与一次调频控制功能都投入的情况下,系统频率动态特性大大提高,接近于原纯同步机系统;如果仅投入一次调频功能,系统的频率特性也有很大改善,非常接近于原纯同步机系统;但如果仅投入惯量支撑控制功能,则较之于普通双馈风机的情况,系统频率动态特性只在达到最低频率点之前有所改善,即延缓了系统频率变化率,推迟了最低频率点的到来,但是在最低频率点之后的恢复过程中,反而恶化了系统的频率恢复特性。

图6给出了仅投入惯量支撑控制功能情况下VSG的电磁功率和机械功率响应情况。

从图6中可以看出,在仅投入惯量支撑控制功能情况下,VSG检测到系统频率快速跌落后迅速增发电磁功率,实现惯量支撑控制;但由于此时没有投入一次调频功能(风机未留备用),导致风机原动机侧的机械输入功率不能增加,在惯量支撑电磁功率的强行作用下,风轮转速将迅速下降,并因为偏离最佳转速,输入机械功率也发生下降,因此将不得不结束短时的电磁功率惯量支撑,甚至需要进一步降低输出电磁功率(低于惯量支撑开始前功率)以避免风机失速停转。总体来看,挽救转速恢复过程中需要降低的输出能量高于惯量支撑期间增发的输出能量(约为支撑能量的1.5～2.5倍),功率恢复时间也长于功率支撑时间,这也正是为什么在图5中仅投入惯量控制情况下反而恶化了最低点之后的系统频率恢复特性的原因。

图6 大电网严重功率缺额事故中VSG 仅投入惯量支撑控制功能情况下的功率响应特性Fig.6 Power response characteristic of VSG only with inertia support control under serious active power shortage contingency in a large power grid

从以上仿真分析可以看出,对于大电网在严重功率缺额事故中的频率动态特性,VSG的惯量支撑功能的作用并不明显,而一次调频功能的作用却较为明显。这是因为:如第3节中所述,惯量支撑作用的主要目的是为一次调频赢得时间,而在大型受端电网中,由于网内同步机数量众多,惯量并不缺乏,因此频率变化率相对较小,到达频率最低点时间长达15 s左右,已经有充足的时间让一次调频发挥作用,再增加惯量支撑也只是锦上添花而已,而且过大的惯量还将使得同样时间内系统的频率跌落幅度变小,从而影响系统内机组一次调频功率的调出,反而不利于系统频率的恢复。所以对于大型受端电网,系统更需要的是VSG的一次调频能力,而不是惯量支撑带来的时间效用。

反之则可以想见,在惯量相对缺乏的新能源高占比的中小型电网与微网中,发生功率缺额时系统频率的跌落速度可能很快,如果没有额外的惯量支撑,一次调频功率可能还来不及调出就已经发生了频率崩溃,这种情况下对于VSG惯量支撑功能与一次调频功能的需求都将比较迫切。

5 结论

1)惯量支撑的功能定位和主要作用是提供可响应于系统频率变化率的短时功率支撑,阻止系统频率快速下跌,从而为一次调频赢得时间,但并不能有效抑制频率的跌落深度。

2)一次调频的功能定位和主要作用是提供可以响应系统频率偏差的持续的有功功率支援,以阻止系统频率的持续跌落,并与负荷的频率效应一起作用,使系统在较低的频率水平上达到新的平衡。

3)在大型同步电网中,系统惯量相对比较充裕,系统频率变化率小,频率变化过程平缓,所以随着可再生能源的接入,由于一次调频能力下降所导致的系统频率动态特性的恶化程度比由于系统惯量下降所导致的更为严重;因此较之于短时的惯量支撑功率,系统更需要VSG发挥一次调频功率的持续支援作用。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 舒印彪,张智刚,郭剑波,等.新能源消纳关键因素分析及解决措施研究[J].中国电机工程学报,2017,37(1):1-9.

SHU Yinbiao, ZHANG Zhigang, GUO Jianbo, et al. Study on key factors and solution of renewable energy accommodation[J]. Proceedings of the CSEE, 2017, 37(1): 1-9.

[2] 陈国平,李明节,许涛,等.关于新能源发展的技术瓶颈研究[J].中国电机工程学报,2017,37(1):20-27.

CHEN Guoping, LI Mingjie, XU Tao, et al. Study on technical bottleneck of new energy development[J]. Proceedings of the CSEE, 2017, 37(1): 20-27.

[3] 李明节.大规模特高压交直流混联电网特性分析与运行控制[J].电网技术,2016,40(4):985-991.

LI Mingjie. Characteristic analysis and operational control of large-scale hybrid UHV AC/DC power grids[J]. Power System Technology, 2016, 40(4): 985-991.

[4] EKANAYAKE J, JENKINS N. Comparison of the response of doubly fed and fixed-speed induction generator wind turbines to changes in network frequency[J]. IEEE Transactions on Energy Conversion, 2004, 19(4): 800-802.

[5] 蒋佳良,晁勤,陈建伟,等.不同风电机组的频率响应特性仿真分析[J].可再生能源,2010,28(3):24-28.

JIANG Jialiang, CHAO Qin, CHEN Jianwei, et al. Simulation study on frequency response characteristic of different wind turbines[J]. Renewable Energy Resources, 2010, 28(3): 24-28.

[6] 丁立,乔颖,鲁宗相,等.高比例风电对电力系统调频指标影响的定量分析[J].电力系统自动化,2014,38(14):1-8.DOI:10.7500/AEPS20130810001.

DING Li, QIAO Ying, LU Zongxiang, et al. Impact on frequency regulation of power system form wind power with high penetration[J]. Automation of Electric Power Systems, 2014, 38(14): 1-8. DOI: 10.7500/AEPS20130810001.

[7] ATTYA A B T, HARTKOPF T. Control and quantification of kinetic energy released by wind farms during power system frequency drops[J]. IET Renewable Power Generation, 2013, 7(3): 210-224.

[8] 隗霖捷,王德林,李芸,等.基于可变系数的双馈风电机组与同步发电机协调调频策略[J].电力系统自动化,2017,41(2):94-100.DOI:10.7500/AEPS20160323009.

WEI Linjie, WANG Delin, LI Yun, et al. Variable coefficient based coordinated frequency modulation strategy between DFIG-based wind turbine and synchronous generator[J]. Automation of Electric Power Systems, 2017, 41(2): 94-100. DOI: 10.7500/AEPS20160323009.

[9] 孙骁强,程松,刘鑫,等.西北送端大电网频率特性试验方法[J].电力系统自动化,2018,42(2):148-153.DOI:10.7500/AEPS20170418006.

SUN Xiaoqiang, CHENG Song, LIU Xin, et al. Test method for frequency characteristics of northwest sending-end power grid[J]. Automation of Electric Power Systems, 2018, 42(2): 148-153. DOI: 10.7500/AEPS20170418006.

[10] 谭放.含大规模风电的送端电网频率稳定控制研究[D].北京:华北电力大学,2016.

[11] ZHONG Qingchang, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.

[12] European FP6 Project Workshop. VSYNC project workshop[EB/OL]. [2017-10-11]. http://www.vsync.eu.

[13] BECK H P, HESSE R. Virtual synchronous machine[C]// 9th International Conference on Electrical Power Quality and Utilisation (EPQU), October 9-11, 2007, Barcelona, Spain: 6p.

[14] 钟庆昌.虚拟同步机与自主电力系统[J].中国电机工程学报,2017,37(2):336-349.

ZHONG Qingchang. Virtual synchronous machines and autonomous power systems[J]. Proceedings of the CSEE, 2017, 37(2): 336-349.

[15] 吕志鹏,盛万兴,刘海涛,等.虚拟同步机技术在电力系统中的应用与挑战[J].中国电机工程学报,2017,37(2):349-360.

LÜ Zhipeng, SHENG Wanxing, LIU Haitao, et al. Application and challenge of virtual synchronous machine technology in power system[J]. Proceedings of the CSEE, 2017, 37(2): 349-360.

[16] 郑天文,陈来军,陈天一,等.虚拟同步发电机技术及展望[J].电力系统自动化,2015,39(21):165-175.DOI:10.7500/AEPS20150508006.

ZHENG Tianwen, CHEN Laijun, CHEN Tianyi, et al. Review and prospect of virtual synchronous generator technologies[J]. Automation of Electric Power Systems, 2015, 39(21): 165-175. DOI: 10.7500/AEPS20150508006.

[17] 黄林彬,章雷其,辛焕海,等.下垂控制逆变器的虚拟功角稳定机理分析[J].电力系统自动化,2016,40(12):117-123.DOI:10.7500/AEPS20150709007.

HUANG Linbin, ZHANG Leiqi, XIN Huanhai, et al. Mechanism analysis of virtual power angle stability in droop-controlled inverters[J]. Automation of Electric Power Systems, 2016, 40(12): 117-123. DOI: 10.7500/AEPS20150709007.

[18] 石荣亮,张兴,刘芳,等.提高光储柴独立微网频率稳定性的虚拟同步发电机控制策略[J].电力系统自动化,2016,40(22):77-85.DOI:10.7500/AEPS20160322016.

SHI Rongliang, ZHANG Xing, LIU Fang, et al. Control strategy of virtual synchronous generator for improving frequency stability of islanded photovoltaic-battery-diesel microgrid[J]. Automation of Electric Power Systems, 2016, 40(22): 77-85. DOI: 10.7500/AEPS20160322016.

[19] 张冠锋,杨俊友,孙峰,等.基于虚拟惯量和频率下垂控制的双馈风电机组一次调频策略[J].电工技术学报,2017,32(22):225-232.

ZHANG Guanfeng, YANG Junyou, SUN Feng, et al. Primary frequency regulation strategy of DFIG based on virtual inertia and frequency droop control[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 225-232.

[20] 陈来军,王任,郑天文,等.改善独立微网频率动态特性的虚拟同步发电机模型预测控制[J].电力系统自动化,2018,42(3):40-47.DOI:10.7500/AEPS20170312003.

CHEN Laijun, WANG Ren, ZHENG Tianwen, et al. Model predictive control of virtual synchronous generator to improve dynamic characteristic of frequency for isolated microgrid[J]. Automation of Electric Power Systems, 2018, 42(3): 40-47. DOI: 10.7500/AEPS20170312003.

[21] 张波,颜湘武,黄毅斌,等.虚拟同步机多机并联稳定控制及其惯量匹配方法[J].电工技术学报,2017,32(10):42-52.

ZHANG Bo, YAN Xiangwu, HUANG Yibin, et al. Stability control and inertia matching method of multi-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 42-52.

[22] 张琛,蔡旭,李征.具有自主电网同步与弱网稳定运行能力的双馈风电机组控制方法[J].中国电机工程学报,2017,37(2):476-486.

ZHANG Chen, CAI Xu, LI Zheng. Control of DFIG-based wind turbines with the capability of automatic grid-synchronization and stable operation under weak grid condition[J]. Proceedings of the CSEE, 2017, 37(2): 476-486.

[23] 刘芳.基于虚拟同步机的微网逆变器控制策略研究[D].合肥:合肥工业大学,2015.

[24] 黄林彬,辛焕海,黄伟,等.含虚拟惯量的电力系统频率响应特性定量分析方法[J/OL].电力系统自动化[2017-02-27].http://kns.cnki.net/kcms/detail/32.1180.TP.20180227.1542.014.html.

HUANG Linbin, XIN Huanhai, HUANG Wei, et al. Quantified analysis method of frequency responding characteristics for power systems with virtual inertia[J/OL]. Automation of Electric Power System[2017-02-27]. http://kns.cnki.net/kcms/detail/32.1180.TP.20180227.1542.014.html.

[25] 王晓声,江浩,刘辉,等.虚拟同步发电机并网稳定性研究综述[J].华北电力技术,2017(9):14-21.

WANG Xiaosheng, JIANG Hao, LIU Hui, et al. Review of the research on stability of virtual synchronous generator under grid-connected operation[J]. North China Electric Power, 2017(9): 14-21.

[26] HUANG Linbin, XIN Huanhai, ZHANG Leiqi, et al. Synchronization and frequency regulation of DFIG-based wind turbine generators with synchronized control[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1251-1262.

[27] HU Jiabing, WANG Shuo, TANG Wenming, et al. Full-capacity wind turbine with inertial support by adjusting phase-locked loop response[J]. IET Renewable Power Generation, 2017, 11(1): 44-53.

[28] 赵杨阳,柴建云,孙旭东.基于虚拟同步发电机的柔性虚拟调速器模型[J].电力系统自动化,2016,40(10):8-15.DOI:10.7500/AEPS20150728014.

ZHAO Yangyang, CHAI Jianyun, SUN Xudong. Flexible virtual governor model based on virtual synchronous generator[J]. Automation of Electric Power Systems, 2016, 40(10): 8-15. DOI: 10.7500/AEPS20150728014.

[29] 李光琦.电力系统暂态分析[M].2版.北京:中国电力出版社,1995:156-158.

[30] 中国国家标准化管理委员会.电网运行准则:GB/T 31464—2015[S].北京:中国标准出版社,2015.

[31] CLARK K, MILLAR N W, SANCHEZ-GASCA J J. Modeling of GE wind turbine-generators for grid studies v4.5[R]. Atlanta, USA: GE Energy, 2010: 44-46.

秦晓辉(1979—),男,通信作者,博士,教授级高级工程师,主要研究方向:电力系统规划运行分析与新技术应用。E-mail： gumpqin@163.com

苏丽宁(1990—),女,硕士,助理工程师,主要研究方向:电力系统规划运行分析与新技术应用。

迟永宁(1973—),男,博士,教授级高级工程师,主要研究方向：新能源并网分析及运行控制技术。