基于ARIMA模型的二手房价格预测

郑永坤，刘 春

(中国电信股份有限公司广州研究院大数据应用研发中心，广东 广州 510630)

0 引 言

近年来，我国房地产交易市场火爆，房价居高不下。2017年8月31日，胡润研究院发布了《2017上半年胡润全球房价指数》[1]，报告中指出，全球房价涨幅前10名中有6个中国城市，而广州是唯一上榜的一线城市。未来广州房价何去何从，很多刚需和投资者也都在观望，房地产市场价格的变化引起了人们的高度重视，而如何准确地预测未来房价的走势将变得尤为重要。

针对房价的预测，目前已有一些学者做了相关的研究。崔庆都[2]和高玉明[3]等采用BP神经网络对房价进行预测，将影响房价的几个主要因素和房价进行相关性分析；王希晶[4]通过对互联网搜索数据的挖掘和分析，构建了基于网络搜索的二手房和新建商品房价格预测模型，对房价指数有较好的拟合和预测效果，但与基本的房价预测模型相比较，加入网络搜索指数后的预测模型改进作用有限；杨楠[5]等结合灰色预测和马尔可夫链预测的优点对房价指数进行预测分析，模型拟合精度较高，但只能应用于较短的时间序列数据。本文采用的ARIMA预测模型，是根据随着时间变化的近5年的历史房产价格，利用差分自回归移动平均来排除其他对房价有影响的复杂因素，诸如人口、经济发展、国家政策等因素，从而找出数据变动的规律，构建一个客观真实的预测模型，来持续预测未来房价的变化趋势。

1 ARIMA模型介绍

ARIMA模型是由博克思(Box)和詹金斯(Jenkins)在1970年代初提出来的著名时间序列预测模型之一，全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model)，也称为博克思-詹金斯法或Box-Jenkins模型[6-7]。记作ARIMA(p，d，q)，AR是自回归，p为自回归项数；MA是移动平均，q为移动平均项数，d为非平稳时间序列转化为平稳时间序列时所做的差分次数(阶数)[8]。

ARIMA(p，d，q)模型是ARMA(p，q)模型的扩展。ARIMA模型的实质是将非平稳的历史时间序列Yt进行d次差分后得到新的平稳时间序列Xt，将Xt拟合成ARMA(p,q)模型，然后再将原d次差分还原，便可以得到Yt的预测数据[9]。其中，ARMA(p,q)的一般表达式为：

Xt=φ1Xt-1+…+φpXt-p+εt-θ1εt-1-…-θqεt-q,φp≠0,θq≠0

当q=0时，ARMA(p,q)模型成为AR(p)模型：

Xt=φ1Xt-1+…+φpXt-p+εt,φp≠0

当p=0时，ARMA(p,q)模型成为MA(q)模型：

Xt=εt-θ1εt-1-…-θqεt-q,θq≠0

ARIMA模型的特点是不直接考虑其他相关随机变量的变化，它将预测对象随时间推移而形成的数据序列当做一个随机序列，并且这个随机序列可以通过自回归移动平均过程来生成，即该时间序列可以由它自身的过去值或滞后值和随机干扰项来解释[10]。如果该时间序列是平稳的，即它的行为不会随着时间的推移而发生明显的变化，那么就可以通过该时间序列的过去值及现在值来预测未来值，这恰恰是随机时间序列分析模型的优势所在[11]。

2 模型构建

通过建立ARIMA(p,d,q)模型进行广州二手房价格预测的基本流程，如图1所示。

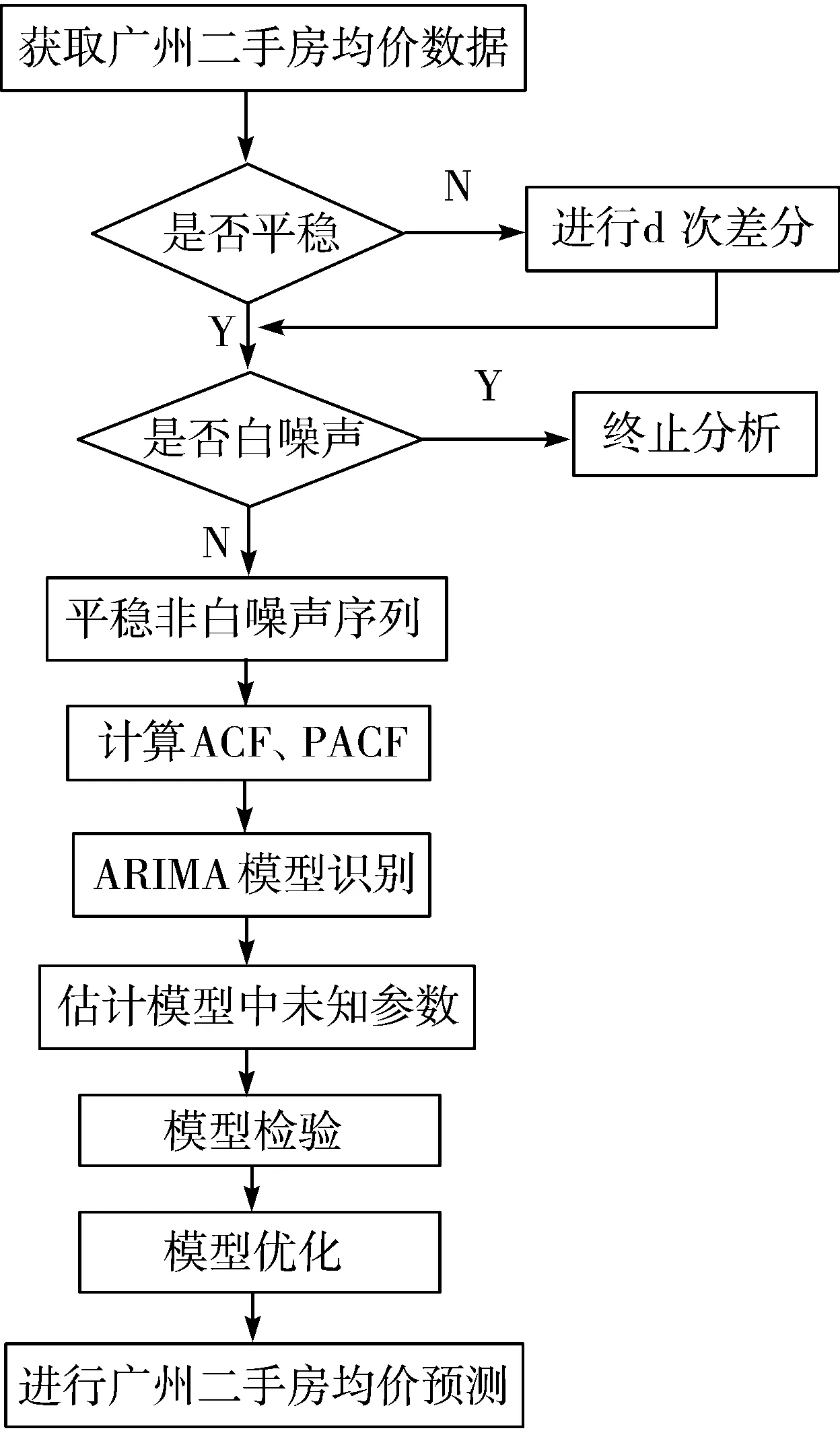
图1 广州二手房价格预测建模流程

2.1 样本数据

本文实验所需的数据是通过国内某知名大型房产网站爬取的[12]。该房产网站是个开放的平台，它集合了各家房产中介的房源信息，且会对房源进行审核，过滤掉价格离谱的房源，最后才从这些房源中统计出均价，通过这种方式得出来的数据是靠谱的，可供参考。经过笔者的观察，房产网站上的均价跟市场上的均价相差无几。因此，本文爬取房产网站上2013年1月份至2017年8月份的广州和深圳二手房历史均价数据作为实验研究基础。

2.2 平稳性检验

首先将广州二手房的历史均价数据作出一个时序图，如图2所示。

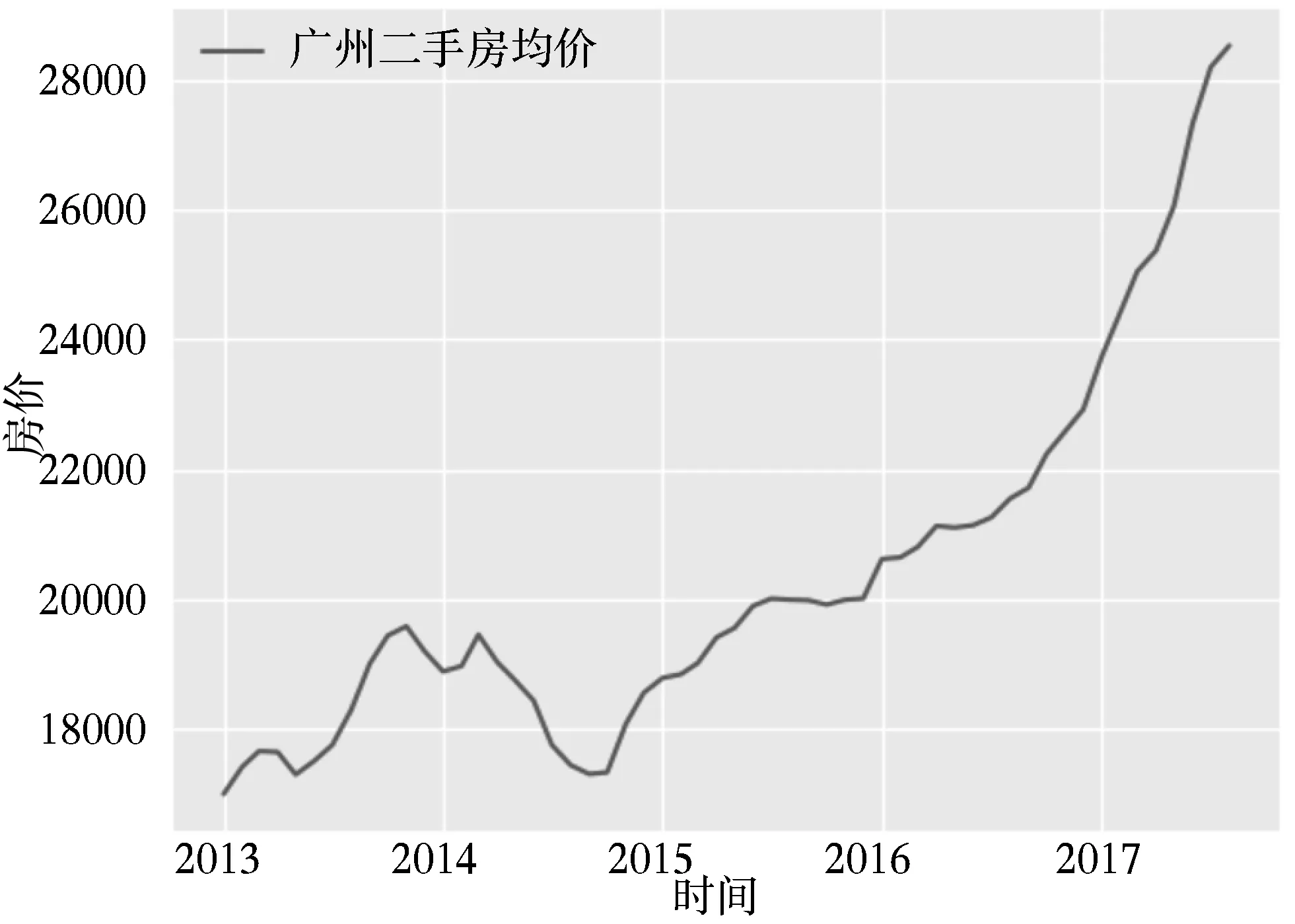
图2 广州二手房均价时序图

显而易见，从2014年底开始，广州二手房价格就一直处于上涨状态，该时间序列基本可视为非平稳时间序列。为了稳妥起见，也可以通过自相关图来验证判断。广州二手房均价自相关图如图3所示。

图3 广州二手房均价自相关图

从自相关图3中可以看到，随着延迟期数的增加，该时间序列的自相关系数并没有很快地衰减向零，而是在零轴一侧上下波动。因此，可以认为该序列是非平稳时间序列。

除此之外，可以利用ADF单位根检验方法[13]来判断序列是否平稳，它的原假设为序列具有单位根，即非平稳。对于一个平稳的时间序列，就需要在给定的置信水平上显著，拒绝原假设。通过计算得出p值为0.99，大于显著水平值0.05，不拒绝原假设，则不通过检验，即存在单位根，该序列为非平稳时间序列。

2.3 序列平稳化

现在对原始时间序列进行一阶差分后再检验，若仍然未通过检验，则需要进行二次差分变换[14]。一阶差分后的时序图如图4所示，可以看到，该时序图并没有明显的趋势，在零附近上下徘徊，可以初步认为它是个平稳的时间序列。

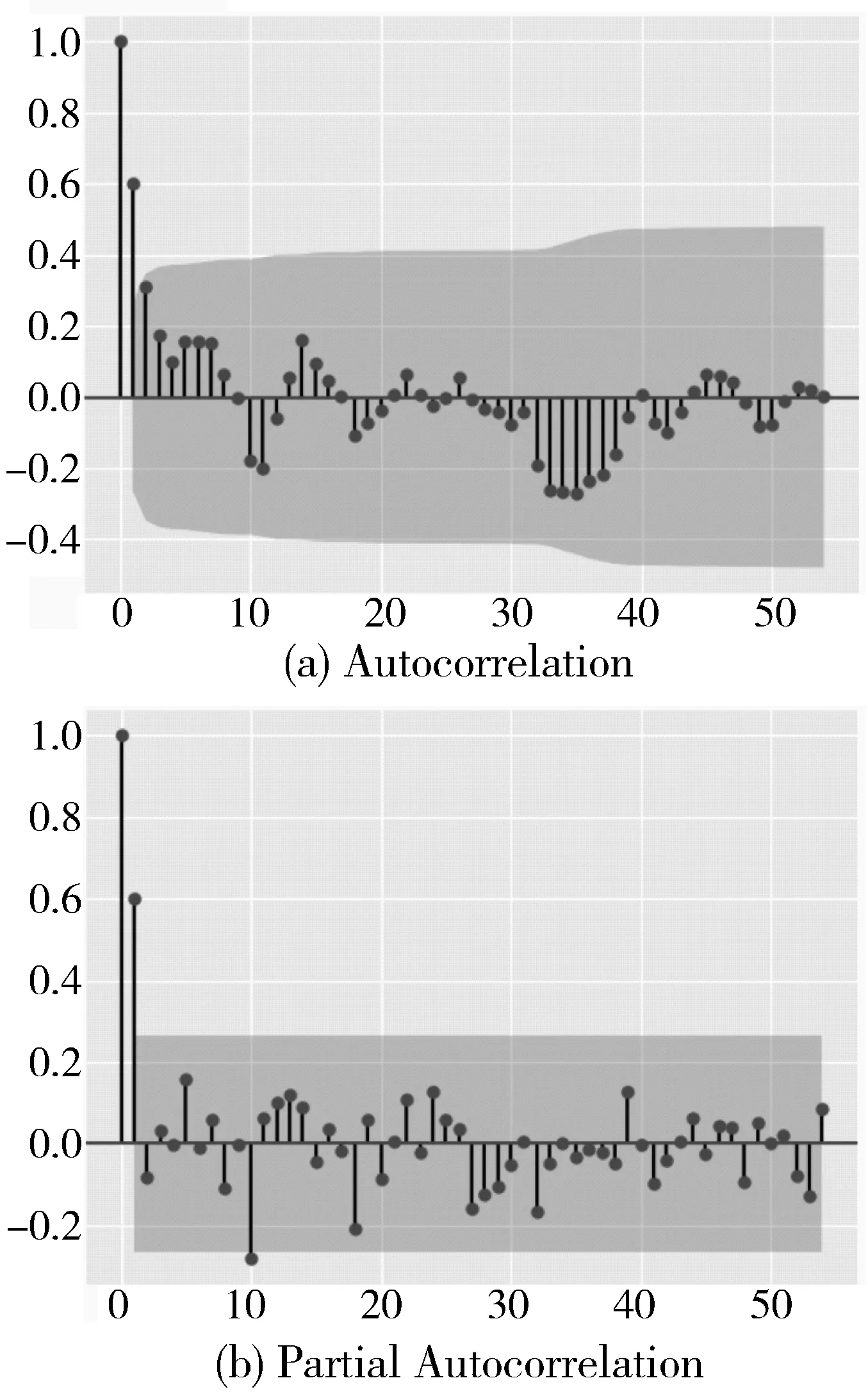
图5 一阶差分后的自相关图和偏自相关图

一阶差分的自相关图和偏自相关图如图5所示，从图5(a)可以看到，该时间序列的自相关系数很快衰减向零，在零附近上下徘徊，没有显著地不等于零，呈现一阶拖尾的自相关性；从偏自相关图(图5(b))中也可以看到，偏自相关系数是截尾的情况，呈现一阶的偏自相关性。

进一步对该时间序列进行ADF单位根的检验，计算出的p值为0.0057，小于显著水平值0.05，也就是说拒绝了原假设，它是一个平稳的时间序列。

2.4 白噪声检验

在对原非平稳时间序列进行平稳化处理后，接下来需要判断差分后的时间序列是否是白噪声，假如是白噪声则没有研究的意义。白噪声是一个纯粹的随机过程，它是严平稳的，其原假设是延迟期数小于或等于m期的序列值之间相互独立[15]。通过计算得出的p值为0.0000046，小于0.05，拒绝了原假设，所以它不是一个白噪声序列。

2.5 模型的识别及定阶

在得出时间序列为平稳的非白噪声序列后，就可以对ARMA模型进行识别，估计模型中未知的参数。由于前面对原时间序列进行了一阶差分，所以d=1，现在需要对p和q进行定阶分析。定阶主要有2种方法：一种是根据自相关图和偏自相关图人为观察识别；另一种是根据信息准则进行识别。

从图5中可以看到，自相关图(图5(a))从一阶后逐渐衰减向零，是一阶拖尾的情况；偏自相关图(图5(b))从一阶迅速降到零附近徘徊，是一阶截尾的情况。当自相关函数拖尾，偏自相关函数截尾时，它是属于AR模型；当自相关函数截尾，偏自相关函数拖尾时，它是属于MA模型；当自相关函数和偏自相关函数均拖尾时，它是属于ARMA模型[16]。根据人为判断，应该建立AR(1)模型，即p=1,q=0。

下面根据BIC准则来识别模型，BIC准则是日本统计学家赤池弘次在AIC准则基础上提出来的一种对数据序列进行建模定阶的方法，是英文Bayesian Information Criterion(贝叶斯信息准则)的缩写[17]。通常来说，在给出不同模型的BIC计算公式基础上，选取使BIC值达到最小的那一组阶数为理想阶数，一般阶数不会超过length/10 (length是数据长度)。首先创建一个空的BIC矩阵，通过循环分别拟合p和q的值，把每次拟合后的BIC值加入矩阵中来，最后从矩阵中找出p和q的最小值。BIC准则拟合出的p和q最小值分别为1和0，跟之前人为识别的结果是一致的，因此建立ARIMA(1,1,0)模型。

3 模型的预测及验证

模型建好后，就可以使用该模型对未来的广州二手房价格进行预测。传统的方式是直接使用该模型预测未来几个月的房价，这样的预测结果并不是建立在近几个月真实房价的基础上的，而是在预测结果上再进行预测。另外本文以滚动的方式使用该模型进行预测，即每个月都把当月的实际房价加入模型当中来预测下一个月的房价。

首先将数据集分为2部分，2013年1月份至2016年12月份的数据作为模型开发数据，2017年1月份至2017年8月份的数据作为模型验证数据。将采用滚动预测后的每个月的预测均价和实际均价都打印出来，并和直接使用模型进行预测的均价进行对比，如表1所示。可以看到，使用模型直接预测未来前一两个月的房价时还算合理，一旦预测超过2个月后的数据将变得不准确，而滚动预测的方式在实践中将会表现出更好的性能。因此，本文采用滚动预测的方式来对房价进行预测。

表1 实际均价和预测均价对比

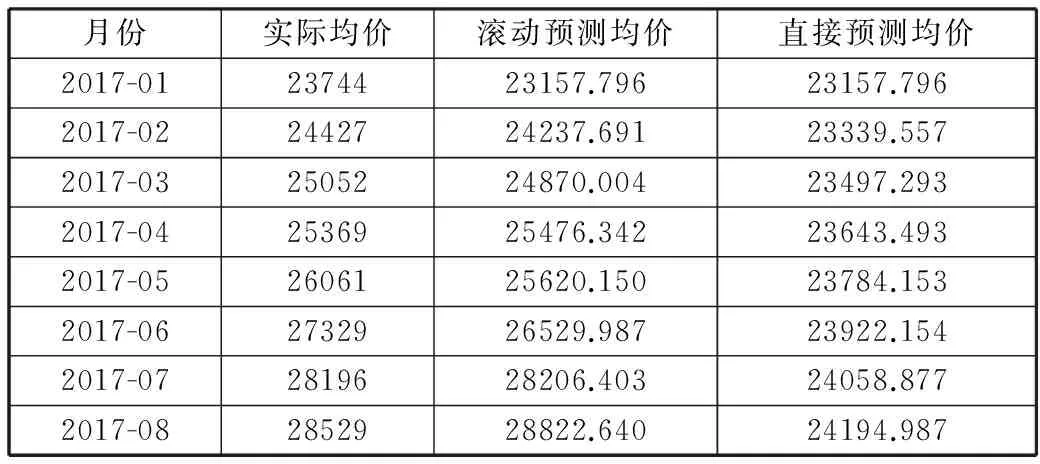
月份实际均价滚动预测均价直接预测均价2017-012374423157.79623157.7962017-022442724237.69123339.5572017-032505224870.00423497.2932017-042536925476.34223643.4932017-052606125620.15023784.1532017-062732926529.98723922.1542017-072819628206.40324058.8772017-082852928822.64024194.987

此外，本文使用均方根误差(RMSE)来衡量预测的精度，它是预测值与实际值偏差的平方与预测次数n的比值的平方根，表达式为：

在本实验中，采用传统的直接预测方法的RMSE值为2729.715，而使用滚动预测方法的RMSE值为409.759，相对上万元的房价来说，几百元的误差是基本可以忽略的，说明该滚动预测模型有良好的性能表现。

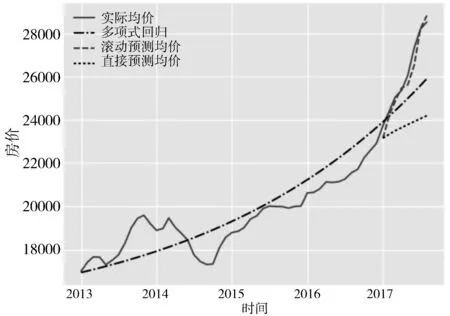
图6 广州二手房实际均价与预测均价对比

与此同时，画出广州二手房均价预测结果与实际结果之间相互比较的图表，并用多项式回归拟合实际结果值，如图6所示，实线为实际均价，点画线为多项式回归拟合，虚线为滚动预测均价，点线为直接预测均价。可以看到，多项式回归只是粗糙地拟合了实际房价曲线，预测结果相差较大，而采用滚动预测方法相比直接预测较好地拟合了实际结果值，具有持续性预测的特性。

上述实验用前4年的数据来预测接下来几个月的数据，虽然验证了模型的准确性，但因为2014年下半年后的数据是呈逐渐上涨趋势，模型的验证还不是很充分。接下来用2014年上半年之前的数据来预测2014年下半年以后的数据的变化趋势，以此来验证该模型对这样有拐点的波动预测的适用性。从图7可以看到，即使数据存在像2014年-2015年前后的巨大波动，该模型依然能够很好地持续预测未来的均价，而采用直接预测或多项式回归预测都与实际均价结果相差甚远。

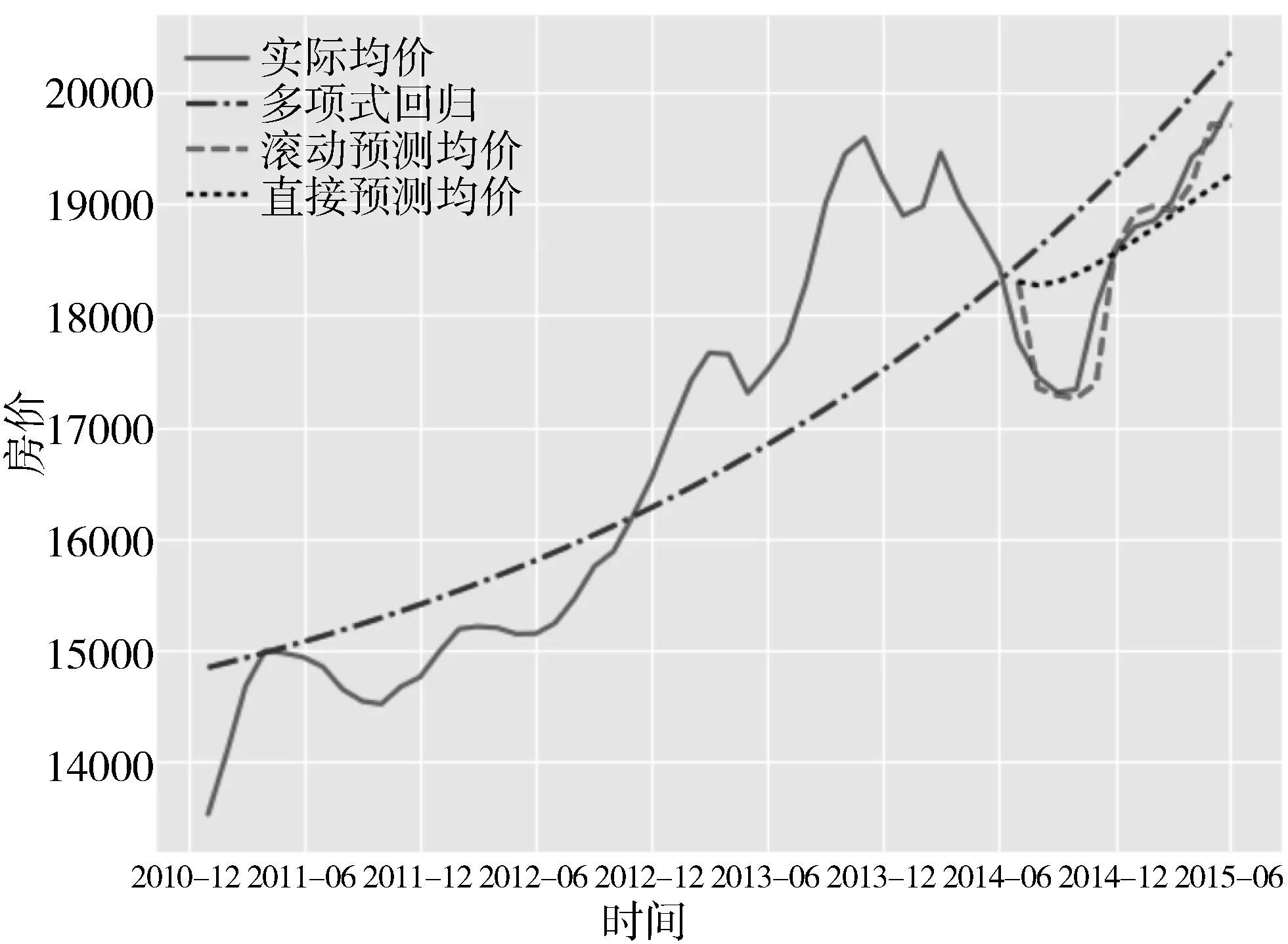
图7 广州二手房实际均价与预测均价波动预测对比

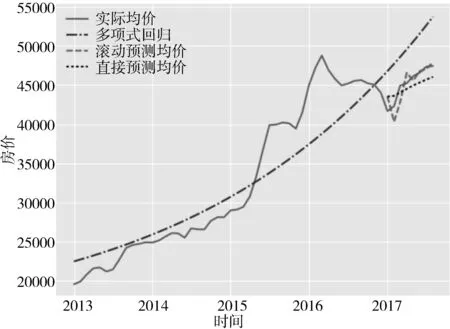
图8 深圳二手房实际均价与预测均价对比

为了验证该模型在其他城市房价预测上的可适性，再选取一个房价波动比较大的城市——深圳来做实验测试。如图8所示，滚动预测方法依然表现出很好的预测性能，该模型仍然可以很准确地预测深圳未来的房价走势。因此，该模型具有普适性，有一定的应用价值。

4 结束语

本文基于时间序列ARIMA模型主要对广州二手房均价进行预测，相比于其他预测方式，排除了一些复杂的影响因素，并使用滚动预测的方法，相比于直接使用模型进行预测，更加客观真实地对房价进行持续性预测，提升了预测的精度。建模中通过BIC准则进行模型的识别及定阶，实验中对2017年广州和深圳的房价进行预测及验证，通过均方根误差及图表的对比，可知取得了显著的预测效果，说明该模型可为房屋买卖者提供有用的参考。

参考文献：

[1] 胡润百富. 2017上半年胡润全球房价指数[DB/OL]. http://www.hurun.net/CN/Article/Details?num=8AD-654C8DF26, 2017-08-31.

[2] 崔庆都. 基于BP神经网络的房价预测[D]. 成都:西南石油大学, 2011.

[3] 高玉明,张仁津. 基于遗传算法和BP神经网络的房价预测分析[J]. 计算机工程, 2014,40(4):187-191.

[4] 王希晶. 基于网络搜索的中国区域房价预测模型及应用研究[D]. 南京:南京大学, 2016.

[5] 杨楠,邢力聪. 灰色马尔可夫模型在房价指数预测中的应用[J]. 统计与信息论坛, 2006,21(5):52-55.

[6] Cryer J D, Chan K S. 时间序列分析及应用[M]. 潘红宇,等译. 2版. 北京:机械工业出版社, 2011.

[7] Brockwell P J, Davis R A. 时间序列的理论与方法[M]. 北京:世界图书出版公司, 2015.

[8] Wikipedia. Autoregressive Integrated Moving Average[EB/OL]. https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average, 2017-09-13.

[9] Tsay R S. 金融时间序列分析[M]. 北京:人民邮电出版社, 2012.

[10] 王燕. 应用时间序列分析[M]. 4版. 北京:中国人民大学出版社, 2015.

[11] 李子奈,潘文卿. 计量经济学[M]. 3版. 北京:高等教育出版社, 2010.

[12] Lawson R. 用Python写网络爬虫[M]. 北京:人民邮电出版社, 2016.

[13] Wikipedia. Augmented Dickey-fuller Test[EB/OL]. https://en.wikipedia.org/wiki/Augmented_Dickey%E2%80%93Fuller_test, 2017-09-19.

[14] Enders W. 应用计量经济学:时间序列分析[M]. 北京:高等教育出版社, 2006.

[15] 百度百科. 白噪声序列[EB/OL]. https://baike.baidu.com/item/%E7%99%BD%E5%99%AA%E5%A3%B0%E5%BA%8F%E5%88%97/8436886, 2017-09-19.

[16] Guo Jianhua. Housing price forecasting based on stochastic time series model[J]. International Journal of Business Management and Economic Research, 2012,3(2):498-505.

[17] Wikipedia. Bayesian Information Criterion[EB/OL]. https://en.wikipedia.org/wiki/Bayesian_information_criterion, 2017-08-01.