基于Levenshtein和TFRSF的文本相似度计算方法

藏润强，孙红光,2，杨凤芹,2，冯国忠,2，尹良亮

(1.东北师范大学信息科学与技术学院，吉林 长春 130117; 2.智能信息处理吉林省高校重点实验室，吉林 长春 130117)

0 引 言

字符串相似问题在自然语言处理、数据挖掘、信息检索等领域，具有非常广泛的应用背景[1]。另外在Google与百度等搜索引擎对模糊关键词查询处理、机器对主观题判卷、论文重复率检测等方面，其相似性问题也一直是需要解决的核心问题。相似的数据信息普遍存在，加上复杂的信息难以区分，严重影响后续数据处理过程，如何判断相似的数据信息一直是自然语言处理、数据挖掘等领域的重要主题之一。例如，不同的社交网络[2]其功能和用户体验都有不同的特点，用户常常在多个不同的社交网络上拥有账户。用户会根据不同的社交网络性质创建一个自身完整形象的局部缩影，由于用户信息分散在各个不同的社交网络，这些分散的局部信息不会相互连通，因此，需要将多个社交网络的账户进行数据拉通。在现实世界中，同一个实体的描述内容总是充满多义性的，人的名字也是其中之一，同一个人名可能被不同人使用，这样导致社交网络中普遍存在的问题是：当查询一个人名时，现有的系统会将所有与该人名同名的结果列出来，这样无疑会使查询用户产生混淆，同名者的个人社会网络往往会出现错误的重叠或合并,针对这些问题，同名相似度匹配的研究工作就显得非常重要。对于姓名重复的用户，通过个人背景信息描述的差异，可以判断是不是同一个人，但是，当描述信息相似，譬如，原有信息的增加或者减少，个人信息简写，信息内容颠倒，计算机会误判为不是同一个人。为了解决这个问题，目前，提出了很多种计算字符串相似度的算法，有字面相似算法、矩阵匹配相似度算法、编辑距离算法等，其中编辑距离[3]算法作为常用的字符串相似度求解算法，在数据清理方面具有一定的优势[4]，在拼写错误检测方面具有较高的精度，具有应用广泛、查找高效和时间复杂度较低等优点。近些年，对编辑距离算法的改进一直在继续，文献[5]中提供了一种归一化的编辑距离。文献[6]中提出了2种计算字符串相似度的公式。文献[7]中提出了一种基于编辑距离和相似度改进的汉字字符串近似匹配算法，通过改进动态规划算法，能够有效提高编辑距离的计算准确度以及执行效率。文献[8]中提出了基于基本操作序列的编辑距离顺序验证方法，不论在长字符还是短字符中都具有更高的效率。文献[9]中使用编辑距离计算2个网络应用程序的相似度，但规定的编辑操作仍不够灵活。

在编辑距离算法的多次改进之后仍然存在若干问题，编辑距离算法没有考虑可能存在字符串位置颠倒问题，这样会导致错误的相似度计算结果。完成2个字符串的编辑距离算法之后需要进行相似度计算，传统的相似度计算方法只考虑了编辑操作次数，没有考虑2个字符串之间的公共子串[10]对相似度的影响。因此，传统的字符串相似度计算方法不具备普遍适用性和准确性。

针对以上文献描述的不足之处，本文根据相关的字符串含有共同词的频率，提出了词频相关字符串频率方法，并改进为一种新的编辑距离方法levenshtein+tf.rsf (lv+tf.rsf)，所提方法的创新之处是融合新的tf.rsf方法处理字符串位置颠倒导致的相似性不准确问题。另外对传统的字符串相似度计算方法进行改进，新的相似度计算方法利用公共子串更适用于编辑距离算法。为了验证所提方法的有效性，使用支持向量机、朴素贝叶斯、随机森林和逻辑回归分类模型[11]进行训练。通过评价指标[12-13]对数据集上进行的文本分类实验结果表明，本文所提出的方法处理字符串相似度更加准确。

1 相关技术与研究

1.1 Levenshtein编辑距离

Levenshtein编辑距离算法是一种计算2个字符串之间的差异程度度量，编辑距离是通过改变源字符串到目标字符串的最小距离。这个距离包括插入、替换和删除等操作，利用动态规划的操作，对每个字符串进行顺序比较，其算法的时间复杂度是O(mn)，空间复杂度为O(mn)，m和n分别表示源字符串S和目标字符串T的长度。

编辑距离D(S,T)的计算方法如下，首先假设Dij=D(S0…Si,T0…Tj),0≤i≤m,0≤j≤n,S0…Si是源字符串，T0…Tj是目标字符串，那么(m+1)×(n+1)阶矩阵Dij可以通过式(1)计算得到：

(1)

式(1)包含删除(wa)、插入(wb)、替换(wc)这3种操作[6]，wa,wb和wc分别表示每一种操作的权重，实验中，删除、插入权重加1，替换权重加2，本文设置wa=1,wb=1和wc=2。

Dij是指从源字符串S到目标字符串T的最小编辑操作次数，目的是计算S与T的相似度，Dij随着2个字符串之间的相似度减少而增加。该算法从字符串左边第一个字符串位置开始比较，对已经比较过的编辑距离，继续计算下一个字符位置的编辑距离。矩阵能够通过从D00逐行逐列计算获取，最终Dmn表示D(S,T)的值，即S和T的最小编辑距离。

例如将“改进编辑距离”转换成“编辑距离改进”，至少需4次编辑操作：删除字符“改”；删除字符“进”；在字符“离”后插入字符“改”；在字符“改”后插入字符“进”。所以，由图1可知，“改进编辑距离”转换成“编辑距离改进”的编辑距离为4。

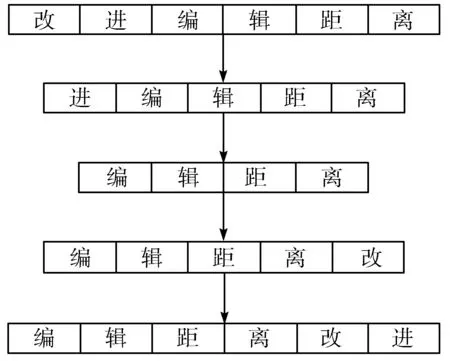
图1 编辑距离过程

1.2 相似度计算方法

得到编辑距离结果后，需要进行相似度计算，相似度是2个字符串之间相似程度的度量，基于编辑距离计算2个字符串相似度的公式[14]为：

(2)

式(2)中，ld表示2个字符串之间的Levenshtein距离；m和n分别为2个字符串的长度；sim值越大，表示2个字符串相似度越高。

2 基于Levenshtein和TFRSF的文本相似度计算方法

由于Levenshtein编辑距离无法处理颠倒的字符串，根据相关的字符串含有共同词的频率，本文提出一种相关字符串频率计算方法，并在其基础上改进为一种新的编辑距离方法levenshtein+tf.rsf。另外结合最长公共子串长度和字符串公共起始位置，对传统的字符串相似度计算方法进行改进。

2.1 词频相关字符串频率

tf.rsf是由词频(term frequency,tf)和相关字符串频率(related string frequency,rsf)这2部分组成的，词频相关字符串频率公式为：

(3)

2.1.1 特征的词频

词频(tf)是指在一篇文档中，某一特征t出现的次数，词频代表当前特征与包含此特征的文档之间的关系。二进制表示是tf的一个特殊形式，如公式(4)所示。

(4)

2.1.2 相关字符串频率的提出

相关字符串频率(rsf)这个命名主要是因为只考虑相关的字符串含有共同词的频率，只有a和b在公式中发挥了作用。下面公式(5)的核心思想为：判断2个字符串是否相似，具有最好区分能力的是那些在2个字符串中同时出现的词。

(5)

在本文提出的“相关字符串频率”中n代表2个字符串含有相同词的数量，a为源字符串的词的总数量，b为目标字符串中词的总数量，x为设定的常数。本文中令x=5，是为了相似度结果更加真实准确。在公式(5)中，max(1,a)和max(1,b)是为了防止源字符串或目标字符串不存在，导致分母等于0的情况。

2.2 两个字符串之间的相似度改进

相似度计算公式(2)并不具备普遍适用性。假设字符串：

S1=“ab”, T1=“bc”, T2=“de”

相似度：

sim(S1,T1)=0.5, sim(S1,T2)=0.5

使用式(2)算得S1，T1的相似度与S1，T2的相似度一样为0.5，但S1，T1的相似度明显大于S1，T2的相似度，因为S1和T1之间存在最长的公共子串b，最长公共子串是字符串S和T的所有公共后缀中长度最大的后缀。本文结合编辑距离和最长公共子串给出改进的字符串相似度计算公式，在改进的相似度计算公式中本文重新定义了2个字符串之间的相似度。本文新的方法使用ld距离、2个字符串的最长公共子串长度LCS(S,T)(longest common substring)和2个字符串比较时第一次出现匹配的字符位置p(position)，引入匹配位置是因为字符串具有顺序性，往往前面的字符相同才会对比后面的字符是否相似，先出现的字符通常代表更重要的信息，所以有必要研究字符的先后顺序对相似度的影响。

(6)

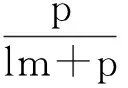
sim(S1,T1)=0.31, sim(S1,T2)=0

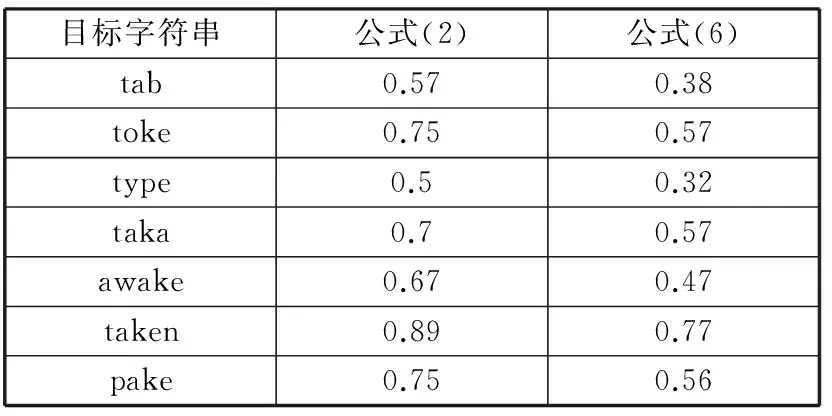
得出S1，T1的相似度大于S1，T2的相似度，比使用式(2)算得的结果更符合实际情况。为了进一步说明，假设源字符串为“take”，表1给出了对不同目标字符串集合，分别使用式(2)和式(6)计算相似度的结果对比。

表1 式(2)和式(6)计算相似度值对比

目标字符串公式(2)公式(6)tab0.570.38toke0.750.57type0.50.32taka0.70.57awake0.670.47taken0.890.77pake0.750.56

由以上例子说明改进的相似度计算公式结果更加真实，公式(6)的结果标准差为0.138，大于公式(2)的标准差0.118，说明公式(6)有着更好的区分度。

2.3 改进的编辑距离算法

同名异义是电子数据库和语义社会网络中普遍存在的问题。比如：在查询一个研究者所发表的文章时，现有的系统会将所有与该研究者同名的作者的文章返回给用户，这样无疑会使用户产生混淆。而语义社会网络中，同名者的个人社会网络往往会出现错误的重叠或合并。针对这些问题，同名排歧的研究工作就显得非常重要。

公式(1)在大多数情况下，从字符串的左边第一位字符开始，依次进行比较，然后记录已经比较过的编辑距离的数值，最后得到下一个字符位置的编辑距离。但是中英文的某些表达方式可以不同，使用公式(1)计算时，却得出错误的结果，尤其是中文的表达方式。

例如S=“大家晚上好”和T=“晚上好大家”，编辑距离为5，相似度为0。实际上S和T表达的意思相同。因此在这种情况下，式(1)不再适用，需要进一步改进。

本文采用的方法是编辑距离和相对频率的融合使用，当2个字符串的相似度小于一定阈值，则使用相对频率进行相似度计算。这样能有效解决因为位置不同导致相似度不正确的问题，改进方法的流程如图2所示，其步骤如下：

1)首先计算字符串的相似度。

2)如果相似度大于或等于设定的阈值，则不进行相对频率的计算。

3)如果相似度小于设定的阈值，进行相对频率的计算。

①如果相对频率计算的值大于或等于阈值，则替换不好的相似度值。

②如果相对频率计算的值小于阈值，仍使用编辑距离计算出来的值。

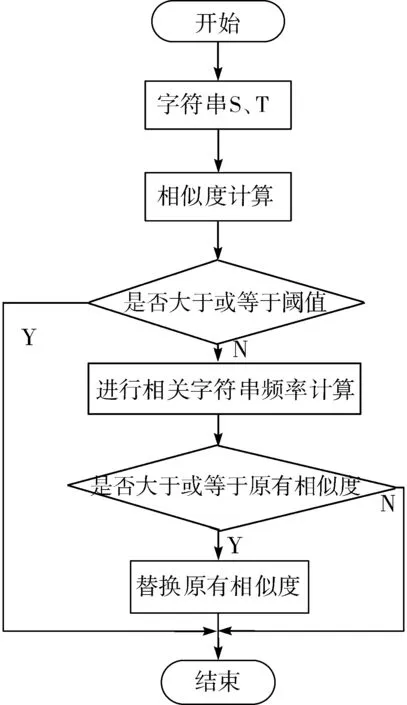
图2 改进方法流程图

3 实验结果及分析

3.1 数据集

为了验证本文所提出算法的有效性，计算不同社交网络中的2个用户信息相似度，判断其是否是同一个人。

图3 一个用户信息抽取例子

首先按姓名搜索出同名列表，使用支持向量机二分类判断是否为用户的个人主页，图3给出了用户的个人主页示例，其中包含了用户的各种信息。例如：图左框的上部包含其姓名、职位、联系电话等，中间部分用自然语言描述了个人经历，下部提供了论文发表情况。其中AMiner利用信息抽取方法[15]自动获取来自学术合作者网络的研究者相关信息，使用爬虫从社交网络LinkedIn爬取用户数据，图3右边显示了理想的结构化抽取结果。在实验前对所有数据进行预处理，包括属性选择、去除停止词、删除标点符号，过滤缺失数据和异常数据后各剩下33957名用户信息。用户的属性包括姓名、单位、教育背景、发表论文、技能、获奖等。

3.2 评价指标及其方法

使用公式(1)和公式(6)计算用户信息相似度,生成特征文件。对于分类问题，目前并没有一种通用的、在任何数据上都能取得最佳分类正确率的算法，因此本文使用Python语言Scikit-Learn库中的支持向量机、朴素贝叶斯、随机森林和逻辑回归分类模型进行训练，用多种分类算法验证算法的有效性。将特征数据切分为5份，每次取其中的1份做测试以及评估，其它4份做训练，循环5次。用准确率、召回率、F1值作为评价指标，对实验结果进行分析。

为了更好地说明评估指标，引入类别列联表。类别列联表针对某一个类别而言，统计了所有测试文本与这个待定类别之间的分类情况。TP(true positive)代表被正确分类到类别C的数量；FP(false positive)代表被错误分类到类别C的数量；FN(false negative)代表实际属于类别C，但是被错误分类到其他类别的数量。

3.2.1 准确率和召回率

准确率(Precision)指的是被正确分类到类别C的数量与被分类到此类别的所有数量的比值。召回率(Recall)是指被正确分类到类别C的数量与实际属于此类别的数量的比值。准确率P与召回率R是分类器性能的2个常用度量值，分别用公式(7)和公式(8)计算。

(7)

(8)

3.2.2 微平均、宏平均

准确率和召回率仅仅可以度量分类器对单个类别的局部分类性能。当对分类器的全局分类性能评估时，通常采用微平均值(Micro-Average)和宏平均值(Macro-Average)。在计算微平均和宏平均的时候，首先需要依据每个类别的列联表得到全局列联表，如表2所示。

表2 全局列联表

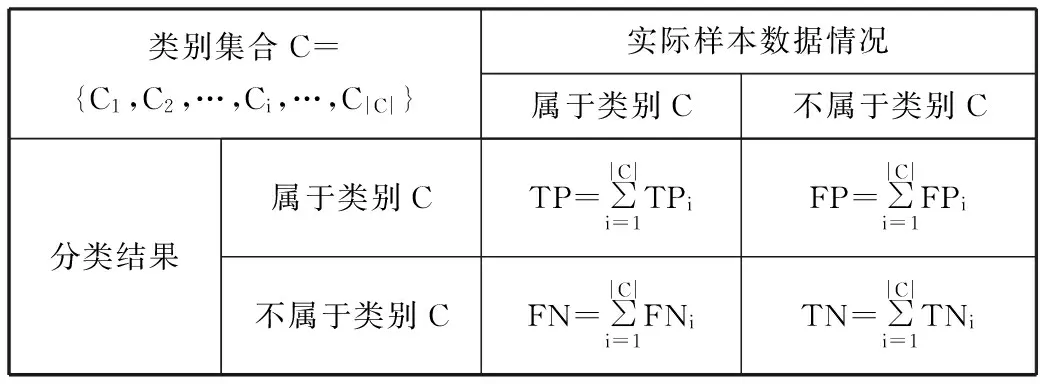
类别集合C={C1,C2,…,Ci,…,C|C|}实际样本数据情况属于类别C不属于类别C分类结果属于类别CTP=∑|C|i=1TPiFP=∑|C|i=1FPi不属于类别CFN=∑|C|i=1FNiTN=∑|C|i=1TNi

宏平均是每一个类别性能指标的算术平均，宏平均在度量的时候，均等对待每一个类别，相比微平均值，宏平均值的结果极易受到小样本类别的影响，微平均是各个性能指标的算术平均，它的值主要受到数据集中较多的类别影响。微平均F1值与宏平均F1值可以综合度量文本分类性能指标。

涉及“生态旅游”这一术语，最早可追溯到1983年，由世界自然保护联盟（IUCN）首次提出，国际生态旅游协会1993年将其定义为：具有保护自然环境和维护当地人民生活双重责任的旅游活动[1]。

3.3 性能比较

将本文提出的方法与其它2组方法组合进行对比分析：

1)使用传统的Levenshtein方法作为本实验的基准相似度方法。

2)邵清在提出的基于编辑距离和相似度改进的汉字字符串匹配算法[7]中，同样考虑到文本位置颠倒位置问题，以语义编辑距离与长句的长度比值作为归一化结果取得了很好的效果，本文使用归一化的相似度计算公式(简称：lv+ssim)作为实验对比。

实验产生的特征文件在多种分类算法下进行微平均和宏平均的准确率、召回率和F1值比较，如表3和表4所示。

表3 微平均性能对比表

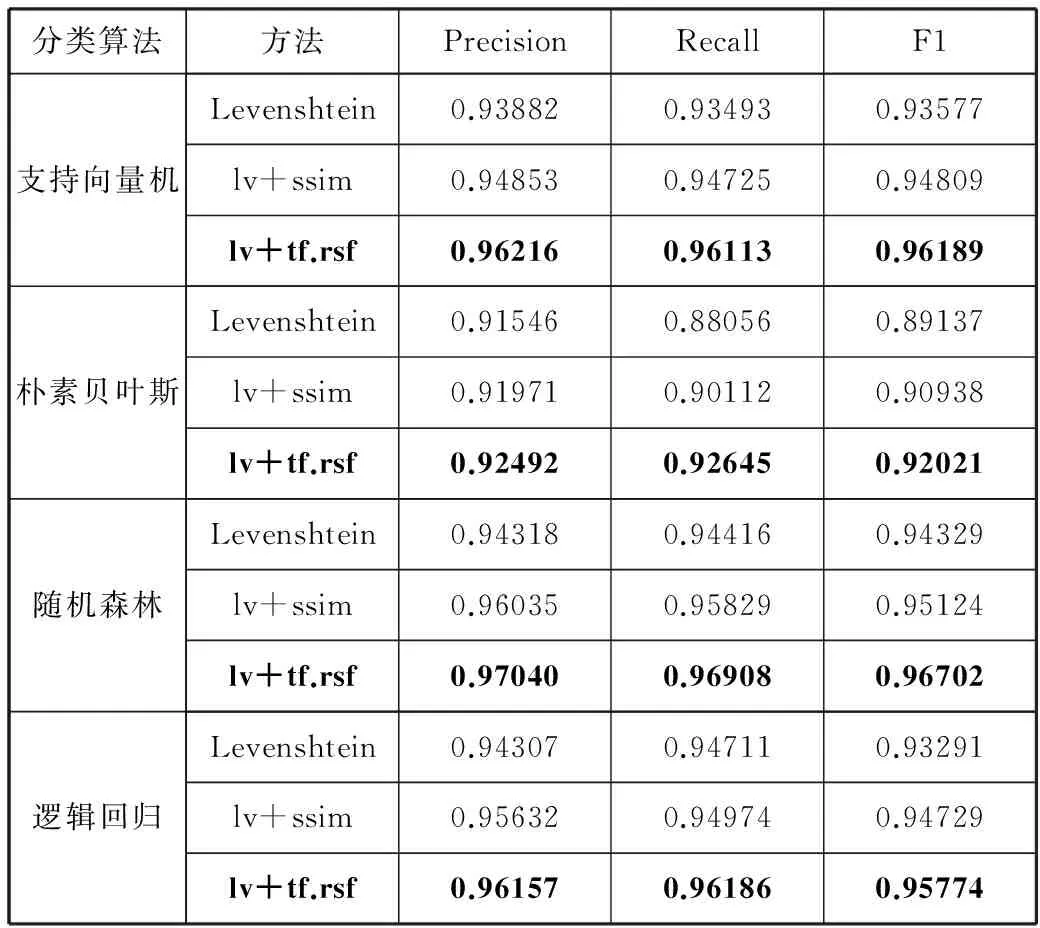
分类算法方法PrecisionRecallF1支持向量机Levenshtein0.938820.934930.93577lv+ssim0.948530.947250.94809lv+tf.rsf0.962160.961130.96189朴素贝叶斯Levenshtein0.915460.880560.89137lv+ssim0.919710.901120.90938lv+tf.rsf0.924920.926450.92021随机森林Levenshtein0.943180.944160.94329lv+ssim0.960350.958290.95124lv+tf.rsf0.970400.969080.96702逻辑回归Levenshtein0.943070.947110.93291lv+ssim0.956320.949740.94729lv+tf.rsf0.961570.961860.95774

表4 宏平均性能对比表

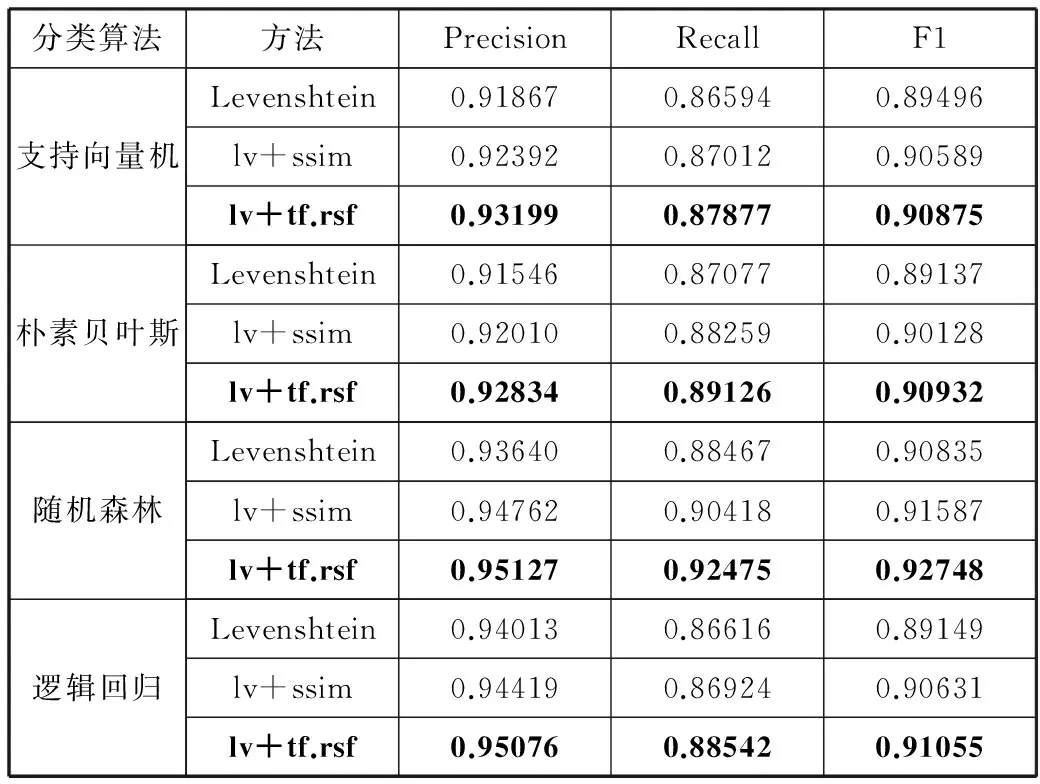
分类算法方法PrecisionRecallF1支持向量机Levenshtein0.918670.865940.89496lv+ssim0.923920.870120.90589lv+tf.rsf0.931990.878770.90875朴素贝叶斯Levenshtein0.915460.870770.89137lv+ssim0.920100.882590.90128lv+tf.rsf0.928340.891260.90932随机森林Levenshtein0.936400.884670.90835lv+ssim0.947620.904180.91587lv+tf.rsf0.951270.924750.92748逻辑回归Levenshtein0.940130.866160.89149lv+ssim0.944190.869240.90631lv+tf.rsf0.950760.885420.91055

图4与图5展示了3种方法在不同分类算法下Precision，Recall，F1这3个指标平均值的对比，实验结果表明本文方法在各项性能指标均优于传统编辑距离和采用归一化的相似度计算方法，并且分类结果具有很好的健壮性。

在这几种分类器中，本文方法的准确率、召回率、F1度量平均值都较稳定，微平均下准确率、召回率、F1度量的平均值均达到0.92以上，说明受到数据集中类别的影响较小。宏平均下准确率平均值均达到0.92以上，召回率平均值均达到0.87以上，F1度量平均值均达到0.90以上，说明模型对负样本的区分能力强，对正样本的识别能力强，分类模型稳定。

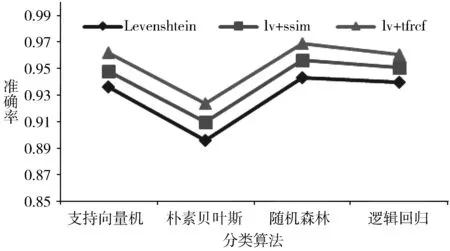
图4 微平均下的Precision、Recall、F1平均值对比

图5 宏平均下的Precision、Recall、F1平均值对比

4 结束语

本文针对相关的字符串含有共同词的频率提出相关字符串频率方法，在Levenshtein编辑距离基础上进行改进，将Levenshtein编辑距离和tf.rsf方法融合，有效地解决了因为字符位置颠倒导致误导决策问题。由于传统的基于编辑距离计算相似度方法普遍适用性低，本文提出的相似度计算方法，提高了计算相似度的准确性。未来将继续优化相似度计算方法，研究更有效的并行算法，并将其用于海量数据处理中。

参考文献：

[1] Gomaa W H, Fahmy A A. A survey of text similarity approaches[J]. International Journal of Computer Applications, 2013,68(13):13-18.

[2] Kwon O, Wen Yixing. An empirical study of the factors affecting social network service use[J]. Computers in Human Behavior, 2010,26(2):254-263.

[3] Levenshtein V I. Binary codes capable of correcting spurious insertions and deletions of ones[J]. Problems of Information Transmission, 1965,1(1):8-17.

[4] 刘辉平,金澈清,周傲英. 一种基于模式的实体解析算法[J]. 计算机学报, 2015,38(9):1796-1808.

[5] Li Yujian, Liu Bo. A normalized Levenshtein distance metric[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007,29(6):1091-1095.

[6] Putra M E W, Suwardi I S. Structural off-line handwriting character recognition using approximate subgraph matching and Levenshtein distance[J]. Procedia Computer Science, 2015,59:340-349.

[7] 邵清,叶琨. 基于编辑距离和相似度改进的汉字字符串匹配[J]. 电子科技, 2016,29(9):7-11.

[8] 张润梁,牛之贤. 基于基本操作序列的编辑距离顺序验证[J]. 计算机科学, 2016,43(S1):51-54.

[9] Popescu D A, Nicolae D. Determining the similarity of two Web applications using the edit distance[C]// Proceedings of the 6th International Workshop on Soft Computing Applications. 2014,1:681-690.

[10] Crochemore M, Iliopoulos C S, Langiu A, et al. The longest common substring problem[J]. Mathematical Structures in Computer Science, 2017,27(2):277-295.

[11] Joachims T. Text categorization with support vector machines: Learning with many relevant features[C]// Proceedings of the 10th European Conference on Machine Learning. 1998:137-142.

[12] Herrera F, Herrera-Viedma E, Martinez L. A fuzzy linguistic methodology to deal with unbalanced linguistic term sets[J]. IEEE Transactions on Fuzzy Systems, 2008,16(2):354-370.

[13] 刘冬瑞,刘东升,张丽萍,等. 基于贝叶斯网络预测克隆代码质量[J]. 计算机科学, 2017,44(4):165-168.

[14] Schumann S, Bühligen U, Neumuth T. Distance measures for surgical process models[J]. Methods of Information in Medicine, 2013,52(5):422-431.

[15] Tang Jie, Yao Limin, Zhang Duo, et al. A combination approach to Web user profiling[J]. ACM Transactions on Knowledge Discovery from Data, 2010,5(1): Article No. 2.