学科能力生根的学习过程优化——试卷评讲前引导学生问题的探究

季 扬

(江苏省泰兴市第一高级中学 225400)

《国家中长期教育改革和发展规划纲要》把“提高质量”作为教育改革和发展的核心任务，提高教育质量，就是要“坚持育人为本、德育为先、能力为重、全面发展”.如何在综合实践活动课程和学科教学中落实“提高质量”和“四个坚持”目标的要求呢(这已是摆在我们每一位教育工作者面前的不可回避的重要课题)？其中，坚持“能力为重”就是要以发展学生的能力为重点，在实践活动中发展学生的学习能力、实践能力和创新能力，注重培养厂大中小学生的终身发展必备的基本能力；坚持“全面发展”就是要在社会实践中感悟个人发展与社会发展息息相关.

一、教学活动中的案例

老师在试卷讲评课后，都会精选一些题目给学生进行有针对性的训练，使课堂上的知识点和解题方法能得以巩固和落实.我认为在试卷讲评课之前，结合试卷中的一些题目，适当地设计一些具有探究性的问题，要求学生通过自己的整理和研究，观察和发现，先行一次拓展.同时，为第二天的讲评能更加贴近学生的实际做好充分的准备，这也是提高试卷讲评有效性的一种好策略.本文，结合自己在一次高三试卷讲评课之前布置的作业题，谈谈几种可行的问题设计形式.

设计一列表整理试题分布、分值及得分情况

问题1 根据试卷题型和得分分布，完善表格

试题类型题号分值得分情况复数运算函数的性质三角运算 ……

设计意图：让学生在数据统计中发现自己在哪些题型上的失分较多，对知识点的把握不到位，可以更好地查漏补缺.教师也能有的放矢地对试卷上错误较多的问题加以讲解，避免一讲到底的现象，或是重复学生会的，而对不会的却没有充分重视.

设计二寻求一题多解

已知圆C：(x-1)2+(y-2)2=2，点P坐标为(2，-1)，过点P作圆C的切线，切点为A,B，求切点弦方程.

问题2 你能尝试用多种解法处理此题吗？

该题是解答题中的第二小问，学生在解决的时候会找不到切入口，若是评讲前让学生先从之前的试卷中对比寻找，或是和同学共同探讨，就会发现该问题的解决方法不止一种，再加以整理对比，寻求最佳解题方法.现对学生整理的反馈如下：

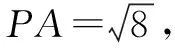
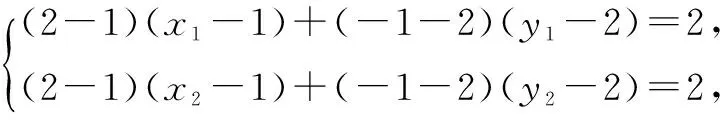
可见点A、点B的坐标都满足x-3y+3=0，

所以直线AB为x-3y+3=0.

设计意图：学生在找不到方法的时候，会觉得能解决问题的都是好方法，殊不知有些题目的思维方式独特，通过探究合作，可以拓展学生思维，培养学生解决问题的能力，老师也能避免出现闭门造车的现象发生，有时候学生的方法比老师的方法更简便，让师生共同收益.

设计三探究错题正解

这道简单的填空题，学生错得比较多.让学生自己根据错解找出问题所在.

问题3 这样解对吗？错在哪儿呢？怎样改正？

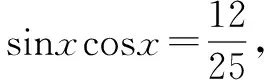
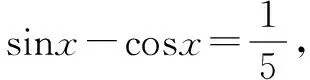
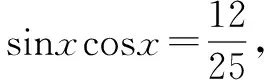
设计目的：学生自己先对错解进行分析，弄清了错在何处，然后找出正确的解答.这个过程其实就是学生再学习、再认识、再提高的过程，它使学生对易出错的知识理解更全面透彻，掌握更加牢固，同时也提高了学生自主学习的能力.

设计四一题多变拓展知识点

已知函数f(x)=x3+ax2+x+b(a,b∈R)在x∈R上是单调函数，则实数a的取值范围是 .

问题4 你能否在不改变函数f(x)解析式的前提下，给出此题一些合理的变式题？

考题是试卷中的一道填空题，利用此题设计了问题4.学生通过比较和联系平时做过的一些题目，给出的变式题还是相当不错的.整理部分如下：

变式①：已知函数f(x)=x3+ax2+x+b(a,b∈R)在x∈R上不是单调函数，则实数a的取值范围是 .

变式②：已知函数f(x)=x3+ax2+x+b(a,b∈R)在x∈(0,1)上是单调增函数，则实数a的取值范围是 .

变式③：已知函数f(x)=x3+ax2+x+b(a,b∈R)有三个单调区间，则实数a的取值范围是 .

变式④：函数f(x)=x3+ax2+x+b(a,b∈R)有极值的充要条件是 .

设计意图：学生在对原题进行变式的过程中会加深对题目已知条件的分析，进一步理解知识点之间的联系，在变化的过程中体会数学的奇妙与艺术，对学习数学产生更加浓厚的兴趣.

设计五通过对比归纳解决同类问题的方法

问题5 怎样通过此题归纳出求不等式恒成立中参数的取值范围的方法？

学生通过过归类大致有这样三种方式：①图象法；②求最值法；③分离参数法.

函数f(x)=3mx2-6(m+1)x+6>0(m<0)在x∈[-1,1]上恒成立，求m的取值范围.

1°-1≤m<0时,f(1)>0.

2°m<-1时,f(-1)>0.

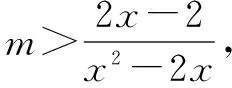
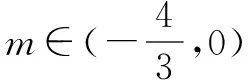
设计意图：学生通过整理，对解决含参数问题的题型加以对比和总结，就能得到解决这类问题的一般方法，这对学生构建知识体系有很大的帮助.

设计六多题同种方法解决

问题6 下面三道都是不同的题目，但也都是求参数的取值范围，你觉得最适合他们的同一方法是什么呢？

题①：函数f(x)=kx-lnx在(1,+)单调增，则k的取值范围是____.

题②：方程x3-3x-a=0有三个不等的实根，求a的取值范围.

题③：不等式x2-mx+1>0在x∈[1,2]上恒成立，则m的取值范围是____.

三道题表面看似毫无关联，但是他们都是含参数的问题，所以分离参数法是比较合适的方法.

我们可以在分离参数后构造新函数，进行求解.

设计意图：分析貌似毫无关联的几题，寻找可用同一方法解题的特征.能让学生在考试中减少思考时间提高解题效率.

试卷评讲的最终目的是让学生纠正错误，避免再次出错.在评讲试卷之前根据试卷大题情况，设置一些引导性的探究性问题，以作业的方式呈现出来，让学生真正体现自主探究和合作学习的实质，也能通过比较找出自己在学习中的优点与不足，培养学习的兴趣与习惯.也极大地提高了教师评讲试卷的效率.

参考文献：

[1]刘长贵.培养学生数学思维能力的几种途径[J].湖南教育，2002(5).