巧用“等号成立的条件”求值问题

苏保明

(云南省蒙自市蒙自一中 (新校区) 661100)

求值问题是多年来高考命制题型的主要内容，由于其题型变化无穷，解决方法多种多样，导致同学们求解起来有一定的难度.其中有一类求值问题是近年高考常考的热点问题之一，在平时的解题中，只要认真分析、仔细思考，就一定能寻找到很多解题思路和方法.

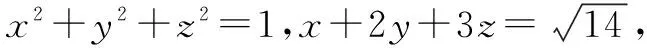
这是一道蕴含着多种解题方法的好题，经过笔者认真思考和研究，给出下面几种解法：

一、判别式法

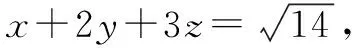
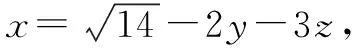
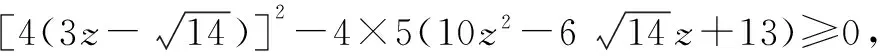
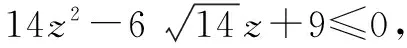
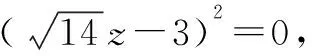
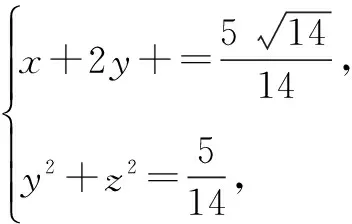
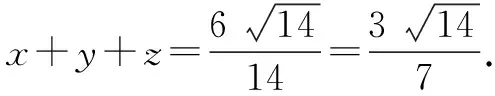
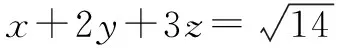
二、利用结论“a2+b2+c2=0⟹a=b=c=0”

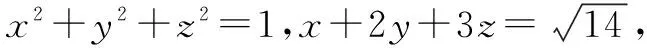
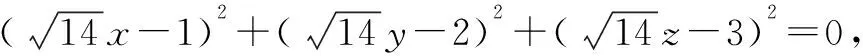
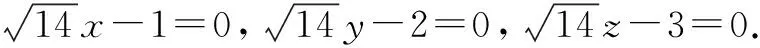
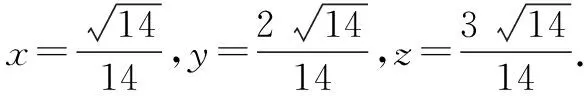
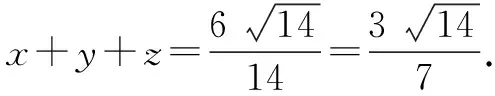
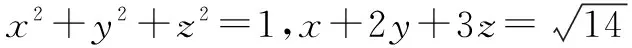
三、利用公式

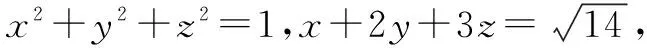
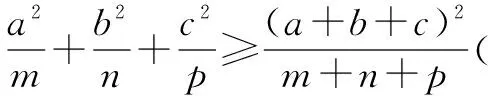
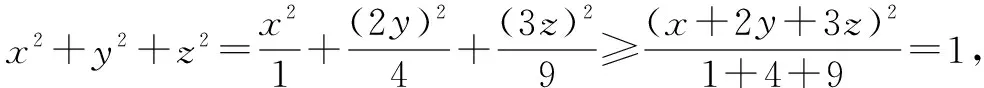
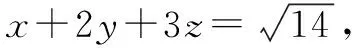
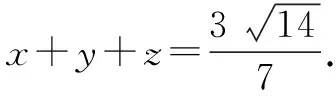
四、向量法

解法4：设a=(x,y,z)，b=(1,2,3)，则由a·b≤|a|b|得

因为x2+y2+z2=1，所以x+2y+3z≤14，所以14≤14.

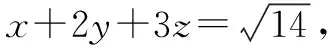
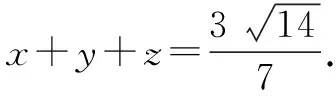
点评用向量法的关键就是正确构造向量a和b的坐标，并使得a·b≤|a||b|中出现x2+y2+z2和x+2y+3z才行.本题是利用向量不等式a·b≤|a||b|中等号成立的条件进行求解.有时向量法是解决某些特殊求值问题的一种新方法.

五、柯西不等式法

解法5 由柯西不等式，得(x2+y2+z2)(12+22+32)≥(x+2y+3z)2.

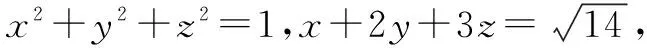
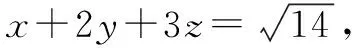
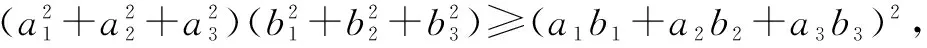
六、化圆法

解法6 由已知得x2+y2=1-z2，

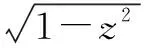
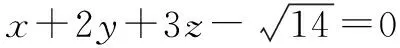
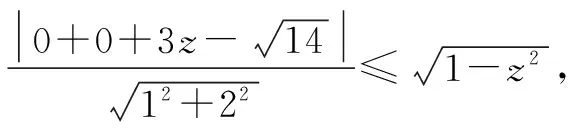
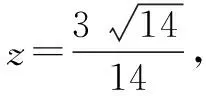
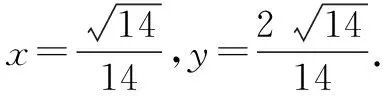
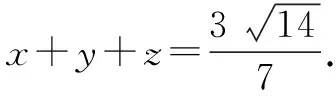
点评构造圆方程解决此题运算过程较为复杂，但这种方法属于通性通法，必须熟练掌握.

参考文献：

[1]人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心. 普通高中课程标准试验教科书( 必修)数学4(A 版)[M]. 北京:人民教育出版社，2014.