抛砖引玉 探索整体法的灵活应用

季韦伟

(江苏省如东中等专业学校 226400)

想要准确的应用整体法来受力分析，进而解析出正确答案，首先要明确是对目标物体受力情况有准确的认识，在此基础上借助具体的例子，目的是来引导学生的解题思路，通过不断地练习和磨合，提高学生解题的效率.

一、结合牛顿第二定律

牛顿第二定律是力学的核心的定义，它普遍运用于力学问题中，如果题目当中有一个或者多个物体组成时，受力分析容易造成混乱而解题失败.这里可以结合整体法来进行分析，让复杂的题目化繁为简.

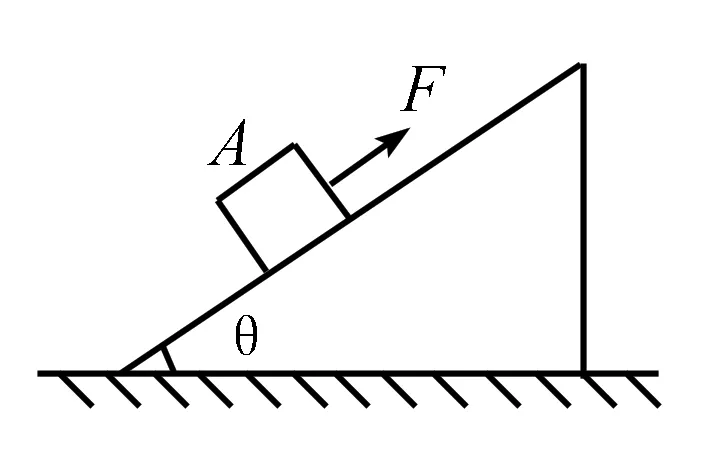
图1

例1 如图1所示的倾角为θ，质量为M.粗糙斜面上，放置质量为m的物体A，用平行于斜面的力F牵引物体A，使物体沿斜面做加速度a的匀加速直线运动，此时斜面静止.求地面对斜面的支持力N和摩擦力f的大小.

解析如果使用常规隔离法来解题，则显得比较繁琐.此时我们采用整体法来解题.对物体A和斜面组成的整个系统来受力分析，受到外力有：重力=(m+M)g，拉力=F，地面的支持力=N，地面所受摩擦力f.将加速度a沿水平和垂直两个方向分解为：ax=acosθ，ay=asinθ，由牛顿第二运动定律知，整个系统水平方向合力向右，且Fcosθ-f=mamx+MaMx,这里amx=ax,aMx=0，得到：Fcosθ-f=macosθ；同时受力分析可得整个系统竖直方向合力向上，且Fsinθ+N-(m+M)g=mamy+MaMy，这里：amy=ay,aMy=0，得到：Fsinθ+N-(m+M)g=masinθ.由以上式子可得：f=Fcosθ-macosθ，N=(m+M)g-Fsinθ+masinθ.

点拨以上题目当中分别对系统整体的竖直方向和水平方向进行受力分析，分析的过程思路清晰，所以不需要分析两个物体间的受力情况，只需要知道合力即可.通过整体受力分析的方法，达到了简化计算，变相降低了题目难度.

二、结合能量守恒

除了普通的单纯的力学问题之外，整体法应用范围还可以扩展到能量守恒以及电磁学等各个方面，考察了整体法的创造性思维，还考察了电磁学的相关知识，是一类非常综合的题目，所以就要注意训练学生的各方面的能力.具体过程可以看下面的例题.

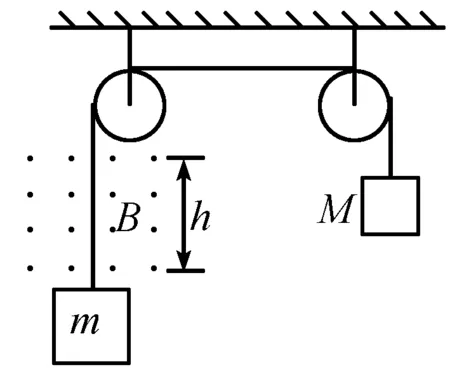
图2

例2 如图2所示，金属材质正方形框边长为l=0.1 m，总质量为m=0.1 kg，回路电阻R=0.02Ω，方框用两个滑轮挂住并在一头加质量M=0.14 kg砝码，线框上方存在均匀磁场，磁场强度B=0.5T(h>l).方框在砝码作用下做匀加速直线运动但是进入磁场后变为匀速直线运动，求方框进入磁场后匀速运动过程中，方框增加的电能.

解析采用整体法进行分析，对方框和砝码组成的系统应用守恒定律，方框匀速上升过程，砝码减少的势能等于方框增加的电能和上升过程增加的势能之和.

Mgl=mgl+ΔE电，所以ΔE电=(M-m)gl.所以将题目的已知条件带入公式得：ΔE电=(0.14-0.10)×10×0.1焦=0.04焦

点拨在这道题当中综合了滑轮组、力学以及电磁学的相关知识，在动态当中受力分析情况比较复杂，走隔离法的途径会比较坎坷.通过解析过程可以看到整体法非常好的体现了它的妙处，结合守恒定律进行整体分析，解题过程的快捷性显而易见.

三、结合动量定理

在力学知识中，不同阶段运动状态不同，是受力分析的难点，每个阶段受力或者运动方式不同，用隔离法计算量就会变得很大.我们通过下面的例题来介绍整体法和动量定理结合的使用技巧，希望能达到开阔学生思维空间的目的.

图3

例3 如图3所示，质量为1.0 kg的小球从20 m的高度自由落体，落在地面反弹上升顶点的高度为5.0 m，小球与地面接触时间为1.0s，在这段时间内小球受到的冲量大小为____(不计阻力，取g=10m/s2).A.10N·S B.20N·S C.30N·S D.40N·S

解析小球自由落体后，经过下落、落地、反弹、到达最高点四个阶段，初、末动量为零，动量没有变化.如图所示，我们把这个过程看过一个整体进行分析.

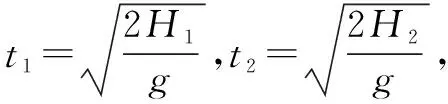
点拨例题当中解题技巧在于把小球下落、落地、反弹、到达最高点四个阶段看作一个整体进行分析，避免了对每个阶段分别进行繁琐，用很小的计算量就得到了正确答案.这种方法值得学生借鉴和学习.

以上三个例题都是在不同的题型当中，应用的共同的解析思维，就是整体法.在恰当的应用之后解题过程大大简化，分析难度也随之降低，通过三个例子做抛砖引玉，目的是让学生在面对问题时有更多的解题选择途径.

参考文献：

[1]周金峰.整体法在解决浮力问题中的应用[J].考试周刊.2012(83).

[2]俞文东.整体法在物理教学中的应用[J].新课程导学.2013(26).

[3]杨成宽.用“整体法”来分析物理问题[J].数理化学习.2009(01).