单位圆在三角函数中的运用

程泓博

(辽宁省调兵山市第一高级中学2年(2)班 112700)

本文主要对三角函数求值、比较大小、确定角的范围及确定函数性质方面做了一些研究，以期作为数学教学及数学研究的参考.

通常在单位圆上，对任意角的三角函数进行定义有以下特点：(1)圆具有对称性，这是其他图形不可取代的，并且单位圆可以简化数学运算步骤；(2)单位圆比较直观，可以将三角函数的奇偶性和周期性直观体现出来；(3)数形结合的思想将单位圆与三角函数性质联系在一起，使得问题的解决变得简单、清晰.

一、三角函数求值

分析如果本题通过直接计算，其方法也很简单，但是如果问题的数量增加，则用直接计算的方法将不易于本题的解决.对于本题的解题方法我们采用数形结合的思想，将单位圆与题意结合起来，使题目的解决思路更加清晰.

二、比较三角函数大小

在一些比较抽象的三角函数关系式大小时，若直接通过计算问题很难得到解决，则需要将问题的解决方式进行转化，使得问题得到简化.其主要转化思想体现在角度、弧度及三角函数问题的相关量的转化过程.

分析对于本题直接运用所学三角函数知识去解题将会增加解题难度，但将数形结合的思想运用到本题当中，则易于解题.本题的难点在于是否具备转化的思想，在解决本题时要将角度与弧度结合起来，则对解决本题有很大帮助.

三、确定变量的取值范围

在使用单位圆解决变量的取值范围问题时，单位圆起着举足轻重作用，它比通常使用的三角函数解题过程更加直观，对解题效率有很大的提高，同时能使读者掌握更多技巧解题的方法.但在用此方法解题时，需要对平面直角坐标系有一定学习基础，并且对坐标系中各个象限的性质及规律能够掌握.

四、确定角的范围

分析对于本题的解决可以通过分情况讨论的思想进行解题，同时通过函数在单位圆上的特征进行解题.

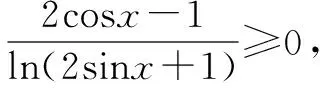
总之,通过本文的研究，我们在利用单位圆解数学题的过程中，应具有如下思路：

(1)利用三角函数的定义与性质，通过与几何图形的直观思想结合，将单位圆作为辅助工具，巧妙解决数学难题；

(2)通过三角函数中角的正弦值、余弦值在单位圆上对应的坐标，结合三角函数及单位圆的性质解决相关数学问题；

(3)充分利用数形结合的思想，运用直观的方法去解题.

参考文献：

[1]王芳芳，胡海光.浅谈单位圆在三角函数中的应用[J].新教师教学，2015(17).

[2]季东升. 单位圆在三角函数中的应用[J]. 高中数学教与学，2010(08).