浅谈阿波罗尼斯圆在高中几何的应用

曾信源

(浙江省温州市龙湾中学高二(9)班 325024)

阿波罗尼斯圆在我们的教材习题以及课外练习中经常出现，甚至有些难题如果我们能够看到它背后命题的本质是阿波罗尼斯圆，那么就会给我们解题带来很大的方便.

一、引例

解析设点M(x,y)，由条件直接列出等式，经化简不难得到点M的轨迹方程是(x+1)2+y2=4，显然点M的轨迹是一个圆.

这是我们数学必修2教材《圆的方程》的一道课后习题，如果把以上的题目推广到一般情形那么就是阿波罗尼斯圆.其实在教材的复习参考题中，是以如下表述形式出现的：

已知点M(x,y)与两个定点M1,M2距离的比是一个正数m，求点M的轨迹方程，并说明轨迹是什么图形(考虑m=1和m≠1两种情形).

我们按照引例的方法建立恰当直角坐标系，就能得到这个圆的方程(m≠1).这个知识点在平面几何和立体几何都有广泛应用.

二、阿波罗尼斯圆在平面几何的应用

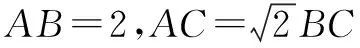
解析这是2008年江苏省的一道高考题，如果按照解三角形的知识去处理，运算会显得很繁琐.如果这道题我们建系去解决，会发现本题的命题背景就是阿波罗尼斯圆.

三、阿波罗尼斯圆在立体几何的应用

图1

例3 如图，平面α⊥平面β,α∩β=l,DA⊂α,BC⊂α,且DA⊥l于A,BC⊥l于B，AD=4，BC=8，AB=6，在平面β内不在l上的动点P，记PD与平面β所成角为θ1，PC与平面β所成角为θ2，若θ1=θ2，则△PAB的面积的最大值是 .

图2

变式练习2 已知平面ABCD⊥平面ADEF，AB⊥AD,CD⊥AD，且AB=1,AD=CD=2.

ADEF是正方形，在正方形ADEF内部有一点M，满

足MB,MC与平面ADEF所成的角相等，则点M的轨迹长度为( ).

提示点M的轨迹是阿波罗尼斯圆，答案为C.

总之，通过以上例题的深刻分析，我认为在平时的数学学习中，如果我们懂得去发现和总结规律，那么我们数学学习就会显得格外轻松，从而能领悟数学的真谛与魅力.

参考文献：

[1]人民教育出版社.普通高中课程标准实验教科书数学必修2教师教学用书[M].北京：人民教育出版社，2007.