对2017年新课标Ⅱ文科第21题的解法探究

刘彦永

(东北师范大学附属中学 130021)

2017年高考新课标Ⅱ文科第21题，题目虽不新颖，但是内涵丰富，引起了笔者的深入探索和思考.题目如下：

设函数f(x)=(1-x2)ex.

(1)讨论的f(x)单调性；

(2)当x≥0时，f(x)≤ax+1，求a的取值范围.

一、试题分析

本题属于传统题，考查了函数的单调性和恒成立问题.以含参数不等式问题为载体，既考查学生的分类讨论思想、等价转化思想、数形结合思想和函数方程及不等式思想，又考查学生分析问题和解决问题的能力.本题由浅入深，对计算难度、思维深度的要求逐步提高，很好地体现了数学的科学性、应用性和创造性.

二、解法探究

本题解法很多，不同的解法体现不同的思维层次和思考角度，要求考生要有一种勇于探索、敢于实践的精神.

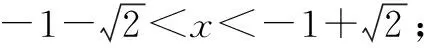
方法一：分类讨论、假设反证法

构造函数g(x)=(1-x2)ex-ax-1，则g′(x)=(-x2-2x+1)ex-a，g″(x)=(-x2-4x-1)ex.当x≥0时，g″(x)=(-x2-4x-1)ex<0，故g′(x)在(0,+)上单调递减，且g′(0)=1-a.

①当1-a≤0即a≥1，x>0时，g′(x)=(-x2-2x+1)ex-a<0，g(x)在[0,+)上单调递减，且g(0)=0，g(x)≤0，即f(x)≤ax+1恒成立.

②当1-a>0即a<1时，g′(0)=1-a>0,且x→+时，g′(x)=(-x2-2x+1)ex-a→-，故存在x0>0使得g′(x0)=0，x∈(0,x0)时g′(x)>0，g(x)在(0,+)上单调递增，且g(0)=0，有g(x)≥0，不符合题意.

综上所述，a的取值范围是[1,+).

方法二：应用分离参数法和洛必达法则

①当x=0时，f(x)=(1-x2)ex≤ax+1即为1≤0·a+1，此时a∈R；

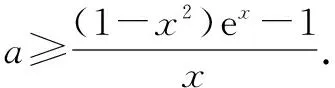
记p(x)=(-x3-x2+x-1)ex+1，则p′(x)=-x(x2+4x+1)ex<0，故p(x)在(0,+)上单调递减，且p(0)=0，故p(x)<0，即在(0,+)上单调递减.

方法三：数形结合

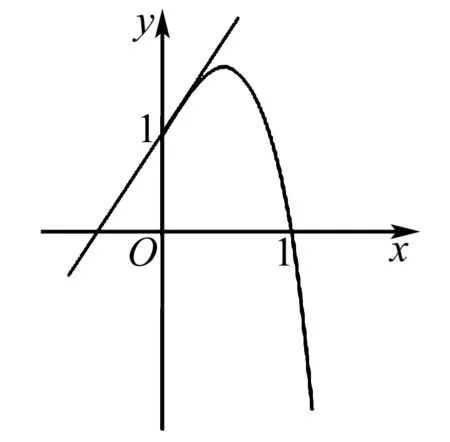
先画出函数f(x)=(1-x2)ex在[0,+)上的草图.

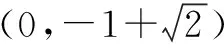
方法四：端点效应

构造函数g(x)=(1-x2)ex-ax-1，则g′(x)=(-x2-2x+1)ex-a.因为g(0)=0，故一定存在x0>0使得x∈[0,x0)时g′(x)≤0.(若不然，即任意x0>0，x∈(0,x0)时g′(x)>0，则x∈(0,x0)时g(x)>0，不符合题意.)从而有g′(0)=1-a≤0，即a≥1. 下面证明a=1时g(x)=(1-x2)ex-x-1≤0 (x≥0)恒成立.由于g′(x)=(-x2-2x+1)ex-1，g″(x)=(-x2-4x-1)ex<0，知g′(x)在[0,+)上单调递减，且g′(0)=0，故g′(x)≤0，g(x)max=g(0)=0≤0， 故a的取值范围是[1,+).

以上解法各有千秋，这样的一题多解能够启发和引导学生从不同的角度、不同的思路，用不同的方法和不同的运算过程去分析和解答试题.

三、考题回顾

新课标Ⅱ文科第21题在2010年和2016年也均考查含参不等式恒成立问题，体现了高考试题“常考常新，推陈出新”的理念.上述四种解法对下面的高考试题均奏效，由于篇幅关系，此处不再赘述.

(2010年高考新课标Ⅱ文科第21题)已知函数f(x)=x(ex-1)-ax2.

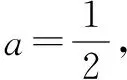
(2)若当x≥0时f(x)≥0，求a的取值范围.

(2016年高考新课标Ⅱ文科第21题)已知函数f(x)=(x+1)lnx-a(x-1).

(1)当a=4时，求曲线y=f(x)在(1,f(1))处的切线方程；

试题解法的探究仅仅是试题研究的一个开端.对解法的探索是在践行我们所学的知识技能和思想方法，同时也使我们的思维更广阔、思想更深刻.对试题本质的探源，使我们更深刻地认识问题，将新旧解题经历跨时空贯通起来，这又是一个新的开始.

参考文献：

[1]华东师范大学数学系.数学分析第四版上册[M].北京：高等教育出版社, 2010.