差比型数列前n项和公式
2018-05-09杨春猛
杨春猛
(云南省玉溪第三中学 653100)
一、问题的提出
处理高中数学中“等差乘以等比”型数列的主要方法是错位相减法,在具体计算过程中计算方法是比较容易掌握的,计算化简过程却比较复杂,很多学生不容易计算出正确的结果,笔者针对这一问题推导出一个方便记忆和计算的公式,以方便大家使用.
二、公式

三、应用
设等差数列{an}的前n项和为Sn,a3=5,S5=25.
(1)求数列{an}的通项公式;
(2)设bn=an2an,求数列{bn}的前n项和Tn.
解(1)略.
(2)由(1)知,bn=an2an=(2n+1)22n+1=(4n+2)4n,
则Tn=6·41+10·42+14·43+…+(4n+2)4n,
4Tn=6·42+10·43+14·44+…+(4n+2)4n+1.
(*)
评析上述公式在使用时的技巧性在于分子的q2往上乘时,等差等比各乘一个q.

例2 设数列{an}的前n项和为Sn,a1=1,且对任意正整数n,满足2an+1+Sn-2=0.
(1)求数列{an}的通项公式;


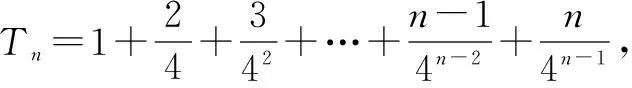

例3 已知数列{an}的前n项和为Sn,(an-Sn-1)2=Sn·Sn-1(n≥2),且a1=1,a2>0.
(1)求a2的值,并证明{Sn}的等比数列;
(2)设bn=(-1)nlog2Sn,Tn=b1+b2+…+bn,求Tn.
解(1)略.(2)由(1)知,Sn=4n-1.
∴bn=(-1)n(2n-2),
四、推导过程
cn=anbn,
所以Sn=a1b1+a2b2+a3b3+…+an-1bn-1+anbn
qSn=a1b2+a2b3+a3b4+…+an-1bn+anbn+1



所以c0=a0b0,就是cn中的n取0时的值.
参考文献:
[1]蓝云波. 差比型数列前n项和的三种求解方法[J]. 中学生数理化:高二高三版, 2016(1):8-8.
[2]于克清. 探究差比型数列求和的方法[J]. 中学数学教学参考, 2016(Z3):82-83.
