不同的稳定性评估方法对量值比对结果的影响

/ 上海市计量测试技术研究院

0 引言

计量比对是指在规定条件下，在相同量的计量基准、计量标准所复现或保持的量值之间进行比较、分析和评价的过程[1]，目前广泛应用于国际互认和实验室能力验证中[2]。传递标准是在测量标准相互比较中用作媒介的测量标准[1]。在多数量值比对活动中，传递标准的稳定性是一个非常重要的考核项目，其实验环境、运输条件等都会对其产生影响[3][4]。本文将以某次上海市冷水水表量值比对活动为例，着重讨论在相同的实验环境下，不同的稳定性评估方法对量值比对结果的影响。

1 测量模型

该模型包含了传递标准的示值误差及其不确定度、稳定性评估和比对结果评价等。

1.1 示值误差

单次测量得到的冷水水表的相对示值误差[5]：

式中：Y—— 单次测量的示值误差，%；

Q—— 实际通过的水量，L；

Qm—— 水表指针的指示水量，L

1.2 不确定度

根据水表检定装置[6]的构成，其不确定度来源主要包括：标准装置、测量重复性、水表分辨力或者激光传感采集、水温等[7]。该测量方法是线性测量模型，可用不确定度传播律[2]来表示：

式中：uc(y) —— 合成标准不确定度；

ui(y) —— 各输入量的标准不确定度

1.3 参考值的确定

本次比对以主导实验室对传递标准的测量值Yn及其不确定度Un作为参考值。Yn为第i个测量点的参考值，Un为Yn的扩展不确定度。

1.4 稳定性评估

传递标准稳定性评估可采用极差法（Range Statistics Method，RSM）或贝塞尔公式法（Bessel Method，BM）[8][9]两种方法。

1）极差法

式中：uei—— 比对期间传递标准在第i个测量点上的标准稳定性；

Yimax—— 传递标准在第i个测量点上测量结果的最大值；

Yimin—— 传递标准在第i个测量点上测量结果的最小值；

C—— 极差系数。

2）贝塞尔法

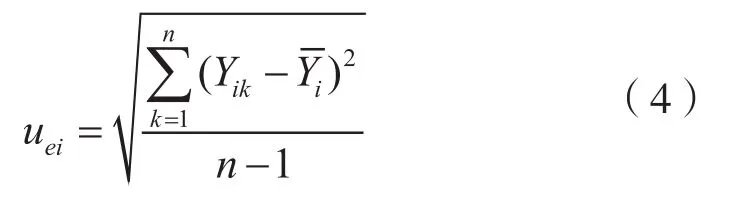
式中：Yik—— 传递标准在第i个测量点上第k次的测量结果；

n—— 实验次数

1.5 比对结果的评价

参比实验室的测量结果依据JJF 1117-2010《计量比对》的中归一化偏差En值进行评价。En值的定义[8]为

式中：Yji—— 第j个实验室在第i个测量点上的测量结果；

Uji——Yji的扩展不确定度；

Uei—— 传递标准在第i个测量点上在比对期间的扩展稳定性

比对结果一致性的评判原则：

2 稳定性评估方法讨论

本次比对以DN20的容积式冷水水表为传递标准，活动历时三个月，时间紧凑，外部环境对传递标准的稳定性影响有限。从式（5）可以看出，传递标准的稳定性是会影响比对评价结果的，如果传递标准不稳定就会使测量不确定度偏大，从而降低比对的效果。为确保误差来源单一，本次比对传递标准的稳定评估数据都是主导实验室严格按照检定规程[9]规定的实验环境测得的。主导实验室对传递标准在常用流量Q3（4 m3/h）和最小流量Q1（0.04 m3/h）下共进行了八次稳定性试验测量，其示值误差如表1所示。

由于传递标准的稳定性可以分别通过RSM和BM得到，本文的重点在于讨论这两种计算方法在稳定性评估时的差异。由式（3）可得到传递标准在极差法下评估的稳定性（如表1中的RSM列），由式（4）可得到传递标准在贝塞尔法下评估的稳定性（如表1中的BM列）。

由表1可以看出，在Q3流量点下RSM和BM通过8次稳定性试验数据计算得的传递标准稳定性分别为0.094 7%、0.095 3%，相对误差仅为千分之六。在Q1流量下传递标准稳定性分别为0.165%、0.162%，相对误差为百分之二。传递标准在Q3流量点的稳定性要好于Q1流量点。比较可知，在一定的实验次数下，这两种稳定性评估方法的结果差异是比较小的，并且这种差异还随着流量的增大而减小。一方面，这说明比对期间针对传递标准的稳定性测量数据是随机的、可靠的。另一方面，也说明了在一定的实验次数下传递标准的稳定性受评估方法的影响是比较小的。

表1 传递标准的稳定性测量数据

3 比对结果的评价讨论

为比较不同稳定性评估方法对参比实验室比对结果的影响，现将由RSM和BM求得的传递标准的稳定性值分别代入式（5），连同各参比实验室的测量数据，可得到不同稳定性评估方法下的参比实验室的En值，如表2所示。

表2 参比实验室的En值汇总表

从表2可知，参比实验室的En值由RSM和BM两种稳定性评估方法得到的结果基本是一致的。这说明在一定实验次数下参比实验室的比对结果几乎不受传递标准稳定性评估方法的影响。

各比对实验室的比对结果，也即测量能力，如图1所示。

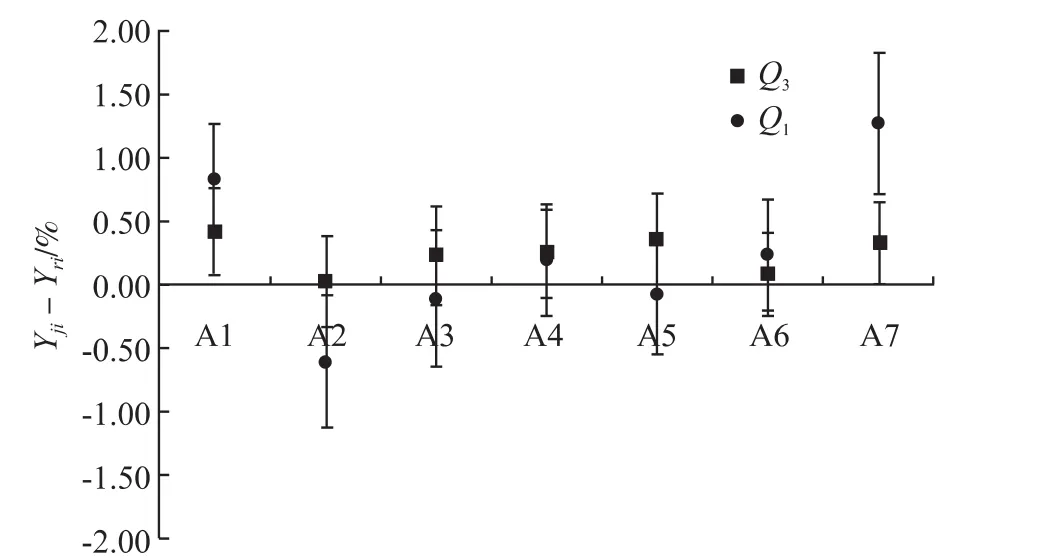
图1 各实验室测量比对结果

图1描述了各实验室的比对结果与参考值的关系，横坐标是参比实验室的代号，图中的小方点、小圆点分别代表各实验室在Q3和Q1流量点的测量结果与参考值之差，即纵坐标Yji-Yri。纵坐标为零的横线为参考值。过小方点或小圆点的垂直正负误差线对应的值是由各实验室扩展不确定、参考值的不确定度和传递标准的稳定性合成得到的，即综合表2和图1可以得出A3、A4、A5、A6实验室的测量结果与参考值之差在合理的预期之内，比对结果可以接受；A1实验室在Q3和Q1流量点的测量结果与参考值之差没有达到合理的预期，A2、A7实验室Q1流量点没有达到合理预期。此次容积式冷水水表在Q3流量点的比对结果满意度要高于Q1流量点。造成参比实验室不满意的原因可能是参比实验室没有严格按照规程要求进行试验，例如水压差异以及其他可能的偶然因素，对此应对标准装置和测量过程进行详细的检查复核。

4 结语

本文建立了比对测量的数学模型，通过贝塞尔法和极差法分别计算了传递标准的稳定性，经比较可知，在一定的试验次数下，这两种稳定性评估方法的结果差异随着流量的增大而减小。再结合某次上海市冷水水表量值比对的结果评价，得出了在一定实验次数下参比实验室的比对结果几乎不受传递标准稳定性评估方法的影响。本文的分析讨论有助于今后更好地开展类似的比对活动。

[1]全国法制计量管理计量技术委员会.JJF 1117-2010计量比对[S].北京：中国计量出版社，2010.

[2]倪育才.实用测量不确定度评定[M]. 北京：中国质检出版社，2014.

[3]赵万星， 廖新 ， 杨有涛 ，等.量值比对中传递标准稳定性评估及作用[J].工业计量，2013（4）：9-10.

[4]石红，舒晓莲.计量比对组织与实施中需关注的问题[J].上海计量测试，2016（3）：60-61.

[5]全国流量容量计量技术委员会.JJG 162-2009冷水水表[S].北京：中国计量出版社，2009.

[6]全国流量容量计量技术委员会.JJG 1113-2015水表检定装置[S].北京：中国质检出版社，2015.

[7]王池. 流量测量不确定度分析[M].北京：中国计量出版社，2002.

[8]全国法制计量管理计量技术委员会.JJF 1059.1-2012测量不确定度评定与表示[S].北京：中国计量出版社，2012.

[9]倪育才.极差法和贝塞尔法之间的比较[J].中国计量，2004（8）：78-79.