部分斜拉桥温度场和温度效应分析

2018-05-09唐自航

四川建筑 2018年2期

关键词：边界条件腹板温差

刁飞，唐自航，黄彪

(西南交通大学土木工程学院，四川成都 610031)

统计大量实际工程发现，温度作用所产生的混凝土箱梁的应力和变形直接影响桥梁结构的安全性、适应性和耐久性。因此，如何准确模拟温度场分布以及研究温度作用下的结构响应是桥梁设计、施工和养护维修的难点和重点。

本文针对处于有剧烈温差变化的某城际铁路矮塔斜拉桥，利用Ansys有限元计算软件，根据天文学基本理论，运用python进行编程模拟该桥梁的日照温度场初始边界条件，对模型进行热分析，分析该桥温度场、应力、应变分布规律。

1 工程背景

1.1 桥梁概况

本文所选取的模型为某城际铁路矮塔斜拉桥，桥跨布置为(97+176+97)m(图1)。

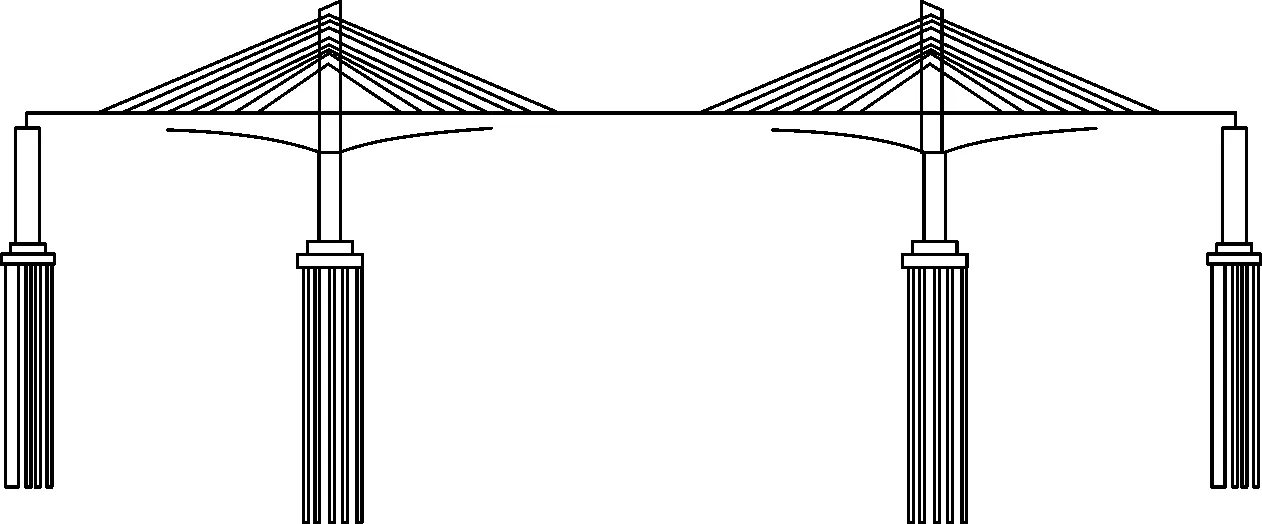
图1 全桥平面示意

该桥主梁采用单箱双室直腹板箱型截面，截面高度采用梁底线型为二次抛物线y=0.0005602x2的高度形式。箱梁边跨梁端和中跨跨中截面梁高均为5.6 m，支座处梁高9.3 m，桥面宽度13.5 m，箱宽11 m(图2)。

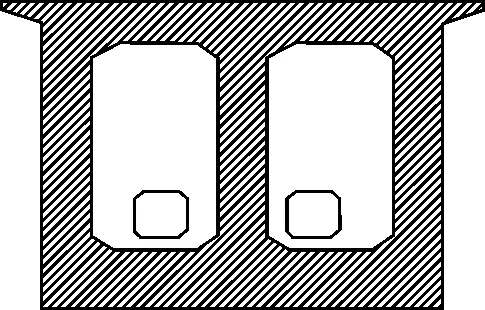
(a)墩顶截面

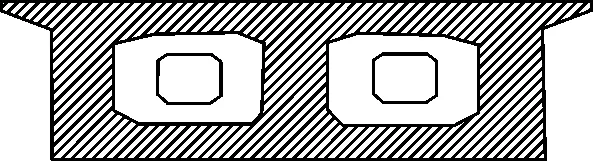
(b)梁端截面

1.2 桥梁有限元模型

通过有限元软件ANYSY建立了箱梁截面的有限元模型，在进行温度场分析时，用PLANE55单元模拟梁截面。PLANE42平面应变单元可以模拟横向纤维与横向框架的约束，用于求解温度自应力与温度次应力。对于纵向次内力的求解采用MIDAS/CIVIL建立梁单元全桥模型，设置对应边界条件，并施加温度梯度荷载。材料参数如表1 。图3为ANSYS二维截面模型，图4为Midas空间有限元模型。

表1 材料参数

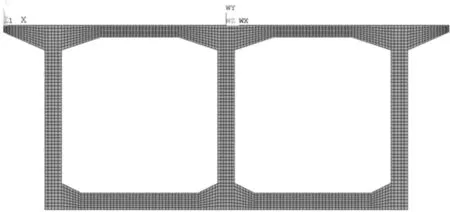
图3 箱梁截面模型

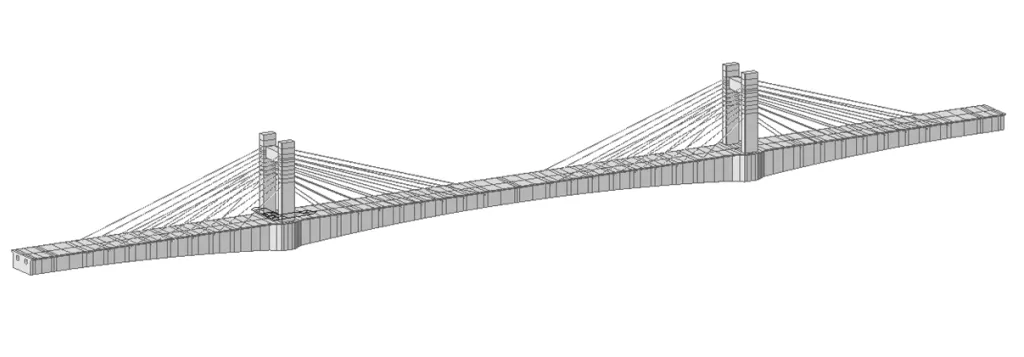
图4 桥梁有限元模型

2 温度场有限元分析

桥梁温度场是与时间、空间相关的四维函数。桥梁结构纵向长度远远大于横向尺寸，并且桥梁跨度内其纵向地理经纬度、风速、气温与太阳辐射强度等变化均非常小，可近似认为没有变化。因此，假定箱梁温度场沿其纵向没有变化，可以把箱梁温度场简化为二维非稳态温度场问题。

2.1 温度场基本理论

本文温度场分析时主要考虑了第二类和第三类边界条件。综合考虑箱梁温度场边界条件的影响因素短波辐射、长波辐射和对流换热。

2.1.1 箱梁温度场边界条件

(1)

ANSYS热分析过程中，不能直接将不同类型边界条件直接叠加计算，需要转换成同一种边界条件，如式(2)中，存在已知热流密度的第二类边界条件和已知热交换系数的第三类边界条件，本文采用将第二类边界条件以第三类边界条件形式表示：

(2)

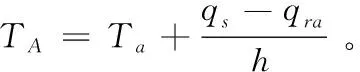
2.1.2 箱梁内部边界条件

箱梁内部边界只存在内壁混凝土与箱内空气的热交换，通常箱梁内部日温度变化较小，且由于处于封闭空间基本无空气流动。因此热交换系数hc按v=0 m/s计算。其边界条件可以表示为：

(3)

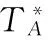
由此可以看出，箱梁温度场边界条件求解的实质就是建立空气介质综合温度数组。

“每一只生肖瑞兽都有独特的个性气质。描绘它们时，我试图摆脱其外在形象的束缚，用心感受亚洲文化，从而在狭小的表盘中展现这些气质。”Anita Porchet表示。“丰富的黑白色调能够创造出细腻的灰色动物毛皮质感，并形成风格低调的背景，凸显狗的昂扬神采。”

2.2 主梁温度场初始温度

本文通过考虑短波辐射、长波辐射、对流换热、阴影长度、日出日落时刻与环境气温等因素，采用编程软件，完成了对顶板、底板、翼缘板底部、不同阴影长度腹板以及箱梁内壁的温度边界条件的建立。对于每个分组得到48个温度点，模拟一天的边界条件，给定10 d为周期，通过重复施加边界条件求解，判断是否收敛。结果如图5，箱梁温度到第4 d以后已经收敛。

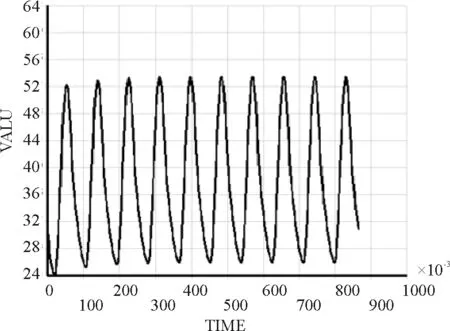
图5 箱梁温度时程曲线

2.3 温度场计算结果分析

为了进一步的体现截面温度场分布情况，选取梁段截面具有代表意义的点做如图6所示的编号。得到关键点24 h内的温度变化时程曲线，分析得出最不利温差时刻，并提取了截面沿梁高与板厚方向的温差分布曲线。

图6 关键点与关键截面编号

在一天内，由于太阳辐射的影响，箱梁会经历升温到降温的过程，白天由于有太阳辐射且混凝土导热性能较差，箱梁表面和内部形成正温差。晚上则相反形成负温差。箱梁内外表面温度的交替升高降低，使得各板均存在两个近似等温时刻，由于辐射的情况不同，各个板出现等温时刻有所差异。

顶板和底板的温度时程曲线如图7、图8。顶板的外部温度波动大于内部，外表面温度变化范围接近24 ℃，内部变化范围不到5 ℃。白天由于顶板不断吸收太阳辐射和环境温度升高，14∶00出现最大正温差，该时刻截面温度分布如图9(c)。夜间由于环境温度降低，箱梁向外部辐射热量，且混凝土导热性能差，到5∶30出现最大负温差，该时刻截面温度分布如图9(a)。由于太阳辐射的影响和气温逐渐升高，顶板外部气温迅速升高，在8∶00左右温度达到内外温度平衡状态。底板关键点温度时程曲线趋势和顶板大致相同，但是由于接受到的太阳辐射小于顶板，内外温度平衡状态的出现时间为9∶00左右，晚于顶板。

由于东腹板在日出时接受太阳直射，外表面迅速升温，不到4 h就达到了一天之内最高温度，并且相比于其它板件最先达到了等温时刻(7∶00)。对于西腹板而言，其整个上午均处于阴影之中辐射强度较小，因此升温缓慢，在10∶30达到内外温度相等，所有板件中最晚，此时截面温度分布如图9(b)。在17∶00时，西腹板出现最高温度，为最晚出现最高温度的板件，对应截面温度分布如图9(d)。中腹板关键点的温度变化不大，这是因为中腹板受到的太阳辐射影响最小。

2.4 最不利温差

箱梁截面进行温度应力分析时，需要确定温度分布最不利时刻。由温度时程曲线可以看出不同部位最不利温差出现的时候。当箱梁外表面温度高于内部温度时，称为正温差；反之成为负温差。本文主要针对正温差，提取最大梁高温差与铁路规范进行对比(图10)。

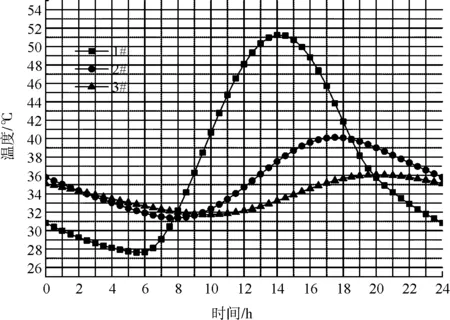
图7 顶板温度时程曲线

图8 底板温度时程曲线

(a)5∶30

(b)10∶30

(d)17∶00

(a)A-A截面

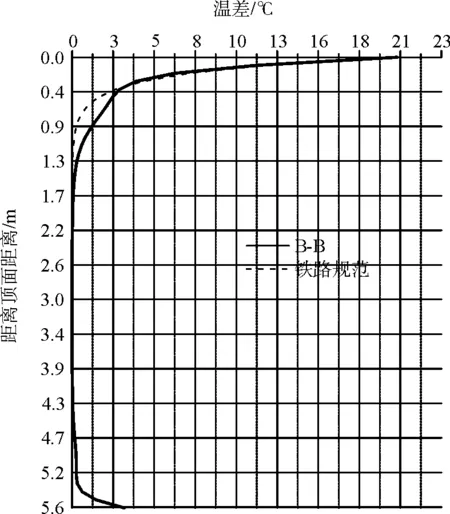
(b)B-B截面

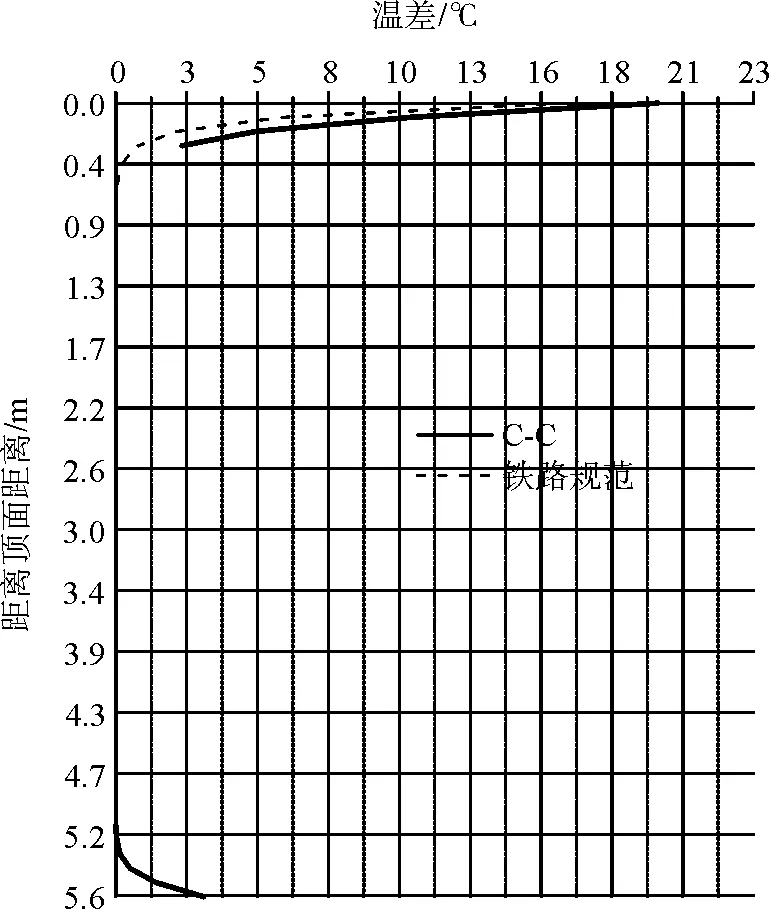
(c)C-C截面

在顶板范围内，截面温差和基本符合规范要求，在腹板范围内，对于东腹板，由于受到太阳辐射的影响，温差略大于铁路规范，在靠近底板处取得最大值1 ℃。铁路规范没有对底板温差做规定，但是可以看出底板也存在3～4 ℃的温差。

腹板最大正温差与按规范计算相差较大，分析原因可能是：规范标准截面在计算沿板厚方向温差时，并未考虑截面方位角、截面倾角与翼缘板对腹板温度分布影响。并且不同箱梁的形状，材料有所差异。

3 结构温度效应分析

混凝土箱梁截面上存在的温度应力按作用方向可以分为横向温度应力与纵向温度应力。纵向温度应力又可以按照产生原因分为纵向温度自应力与纵向温度次应力；同理横向温度应力也可以分成横向温度次应力与横向温度自应力。横向温度次应力是由于截面横向框架约束引起，纵向温度次应力则是由于桥梁本身存在的多余约束引起。

计算求得箱梁截面各个时刻温度场分布之后，将热分析单元转换成结构分析单元以完成横向温度应力与纵向温度自应力的求解(图11)。

(a) σx

(b) σy

由于顶板和腹板接受太阳辐射值较大，因此高应力区主要集中在顶板和腹板位置。箱梁截面水平温度应力主要集中在顶板位置，竖向温度应力主要集中在外腹板，其他位置所受应力较小。在沿梁高度方向最大正温差作用下，在13∶30到17∶00左右，桥梁横向的最大水平拉应力达到了3.61 MPa，最大竖向拉应力达到1.2 MPa。在沿梁高度方向最大正温差作用下，纵向温度自应力最大值为4.67 MPa，其最大拉应力位置出现在翼缘板拐点上，分析原因是由于拐点处于双向传热状态，加之尺寸较小，因此温度变化幅度较大，使其纵向温度自应力明显高于箱梁截面其它位置。这也与翼缘板拐点经常出现混凝土脱落这一普遍现象相吻合(图12)。