龙河大桥地震响应时程分析

高金亮, 杨 俊

(四川省交通运输厅公路规划勘察设计研究院, 四川成都 610041)

1 工程概况

丽江至攀枝花高速公路龙河大桥半幅宽12.5 m，上部结构采用18×30 m简支T梁，下部结构采用双柱式墩，由于桥位处地形变化较大，本文选择桥墩高度最高的一联第8-11

孔做抗震分析，第7-11号桥墩高度依次为：45.5 m、47.5 m、40 m、34 m、30 m，由于7号墩顶为滑板支座，其地震作用较小，本文选取最不利的8号桥墩进行地震响应时程分析，桥梁立面图见图1所示。

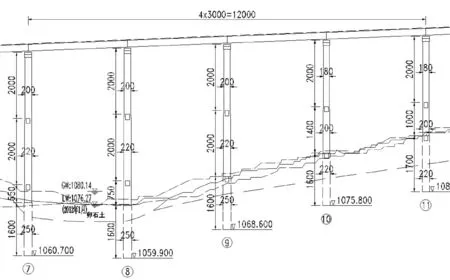
图1 桥梁立面

2 地震参数取值

本桥地震动峰值加速度为0.1g，反应谱特征周期为0.45 s，场地类型为II类，属于高速公路上的桥梁，为B类桥梁。根据《公路桥梁抗震设计细则》，桥梁抗震设防措施等级为8级。

3 计算模型及计算方法

采用Midas Civil有限元软件建立全桥三维空间杆系模型，进行地震响应时程分析。中墩采用板式支座，联端采用四氟滑板支座，所以模型中没有建立联端桥墩；支座纵、横向的剪切刚度均采用弹性连接进行模拟；桥墩桩基采用“m”法(土弹簧)模拟，在软件中通过节点弹性支撑来实现。

4 地震响应时程分析法

本桥8号桥墩最大墩高47.5 m，已大于《公路桥梁抗震设计细则》规定的30 m，属于非规则桥梁，需采用时程分析法进行抗震分析。通过时程分析法可以计算出地震过程中每一瞬时结构的位移、速度和加速度反应，较为准确的计算出结构在地震过程中的内力和位移随时间的反应，并发现结构在地震过程中可能存在的薄弱环节或可能发生的震害，是计算地震反应较为真实的精细分析方法。

依据本桥所在的场地类型，根据GB 50011-2001《建筑抗震设计规范》的规定，选取两组实际强震记录和一组人工模拟的加速度时程曲线，将三组数值取平均后与振型分解反应谱法所采用的地震影响系数曲线做比较，得出与本桥适用的地震波。幅值的调整：

(1)设计加速度峰值PGA的求法：

PGA=Smax/2.25=CiCsCdA

(2)E1地震时程缝隙所用地震加速度时程曲线的最大值：

PGA1 =CiCsCdA=0.5×1.3×1.0×0.1×9.8

=0.637 m/s2

(3)E2地震时程缝隙所用地震加速度时程曲线的最大值：

PGA2 =CiCsCdA=1.7×1.3×1.0×0.1×9.8

=2.1658 m/s2

调整后的地震波如图2所示。

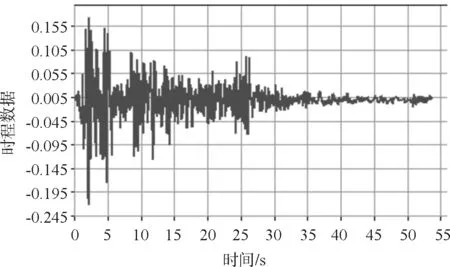
图2 调整后的地震波

(4)地震波特征周期Tg的确定。

因为拟相对速度反应谱PSV和拟绝对加速度的反应谱PSA之间有近似关系PSA=W·PSV，则可以得到特征周期：

Tg=2π(1/w)=2π(EPV/EPA)

其中：EPA为有效峰值加速度；EPV为有效峰值速度。

可求得EPA及EPV的对数坐标如图3、图4所示。

图3 EPA的对数坐标

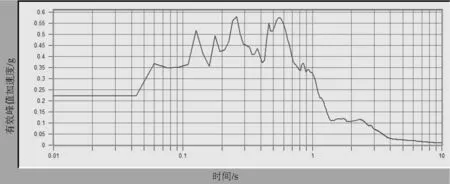
图4 EPV的对数坐标

EPV=0.38 m/s；EPA=4.8 m/s2

Tg=2π(EPV/EPA)=2π(0.38/4.8)=0.49742 s

该桥所在场地地震特征周期为0.45 s，与实录特征周期0.497 42较为接近，故实录波的特征周期适用于本桥。

5 时程分析法计算结果

采用集中铰弹塑性梁单元对桥梁延性构件桥墩进行模拟，在E2地震作用下对桥墩进行Pushover分析，可以得到墩底截面的弯矩-转角关系曲线，以及桥墩的最大弯矩、轴力、墩顶最大位移等。

墩底弯矩(图5)在2.24 s达到最大值16 600 kN·m，在12.31 s达到最小值-10 250 kN·m。

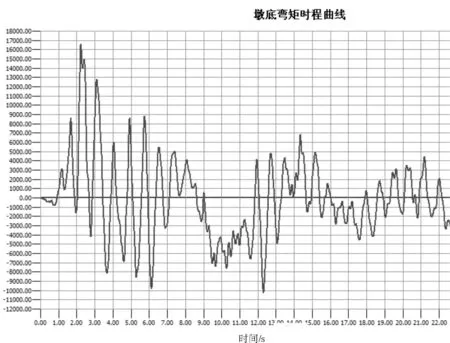
图5 墩底弯矩时程曲线

在地震作用激励下，墩顶位移(图6)在2.46 s时达到最大，最大值约22.7 cm。

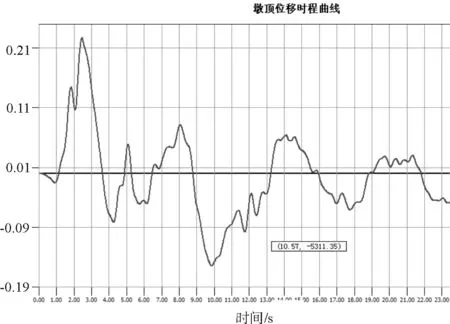
图6 桥墩墩顶位移时程曲线

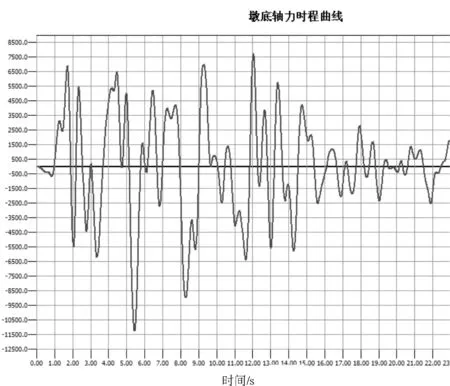
图7 桥墩墩底轴力时程曲线

桥墩墩底转动角(图8)在2.24 s时达到最大转角0.001 213 rad。

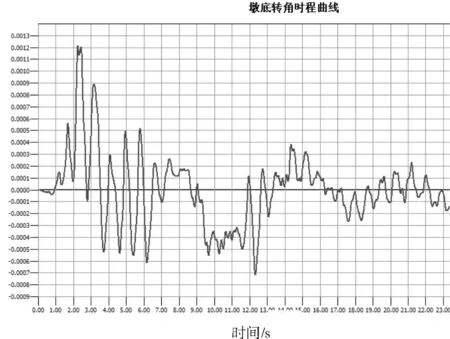
图8 桥墩墩底转角时程曲线

通过图5～图8可以清晰的看到在地震过程中桥墩的弯矩、轴力、转角、墩顶位移随着时间变化，并发现在2.24 s附近桥墩的受力最不利。

塑性铰区域的塑性转角计算过程如下：

Lp1=2/3×b=2/3×250=166.7 cm

Lp2=0.08H+0.22fyds=466.4cm>0.044×400×2.8=49.28 cm

Lp取166.7 cm

圆形截面的等效屈服曲率Φy：

ΦyD=2.213×0.002

Φy=2.213×0.002/2.2=0.00177(1/m)

圆截面的极限曲率Φu：

(1)ΦuD=(2.826x10-3+6.850εcu)-(8.575x10-3+18.638εcu)(P/fc/Ag) =0.0328

(2)ΦuD=(1.635x10-3+1.179εs)-(28.739xεs2+0.656εs +0.010)(P/fc/Ag)=0.08

取两者中的较小值：

Φu=0.0328/2.5=0.013135

塑性铰区域的最大容许转角θu

=Lp(Φu -Φy)/K

=166.7/100x(0.0328-0.00177)/2=0.00947

根据共轭梁法可求得整个桥墩构件潜在塑性铰区域的塑性转角θp

θp=0.003874+0.000282+0.000022=0.0042

θp <θu，满足规范要求。

Δ容=1/3x27.52×0.00177+(27.5-166.7/2)x0.00947=0.797m

Δ=22.7cm<Δ容=79.7cm

通过计算可以得出顺桥向的最大曲率小于墩底截面的屈服曲率，即地震作用下墩底截面并未进入屈服状态；桥墩墩顶位移小于容许位移值；从墩底截面的弯矩-转角滞回曲线(图9)可以看出桥墩在地震作用下墩底截面有开裂现象发生。

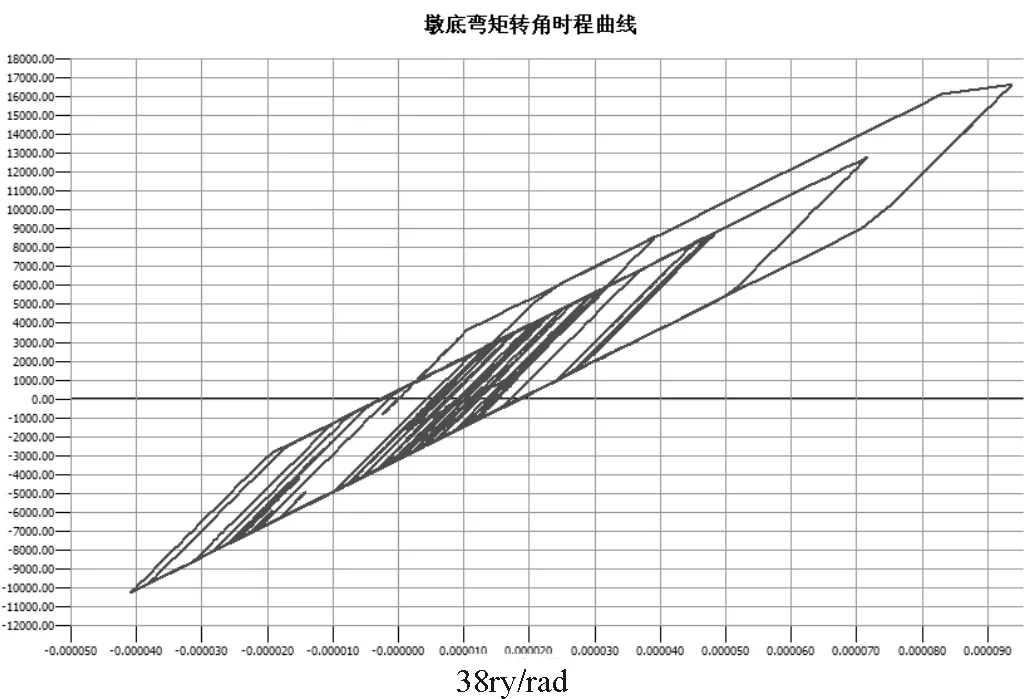
图9 墩底截面的弯矩-转角关系曲线

6 结束语

本文对高墩桥梁下部结构采用时程分析法进行地震分析，桥墩墩顶位移、墩底截面转角等均小于规范的容许值；本文时程分析法选取地震波的过程及通过Pushover进行塑性分析，对非规则桥梁的抗震分析具有指导意义，可供广大桥梁工程设计者借鉴。

[1] JTG/T B02-01-2008《公路桥梁抗震细则》[S].

[2] JTG D62-2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[S] .

[3] 范立础. 桥梁抗震[M].上海:同济大学出版社，1997.

[4] 范立础，卓卫东. 桥梁延性抗震设计[M]北京：人民交通出版社，2001.