基于非均匀压力分布形式的预应力摩阻损失计算

2018-05-09陈谦

四川建筑 2018年2期

陈谦

(中铁十二局集团第七工程有限公司，湖南长沙 410004)

在施加预应力时，预应力大小并不是一成不变的，需要准确估算预应力损失值。而在引起预应力变化的因素中，预应力的孔道摩阻损失占很大一部分[1]。其取值合理与否不仅影响预应力混凝土构件的变形，甚至还会影响到结构的耐久性和承载力。如果预应力摩阻损失计算取值不准确，就会影响预应力损失的估计，而预应力损失估计不足会使得混凝土的实际压应力储备偏低，是造成大跨度预应力混凝土连续箱梁腹板开裂、跨中下挠的主要原因之一。高速铁路桥梁多采用预应力混凝土梁结构，由于行车速度快，对轨道平顺度要求极高，如果预应力摩阻损失计算取值不准确，不可避免地会影响梁体后期徐变预测的准确性，导致轨道的竖向平顺度超过规范要求，不仅给后期的维护带来困难，甚至影响行车安全[2]。因此，研究预应力孔道摩阻损失的计算方法具有很重要的实际意义。目前关于预应力孔道摩阻损失计算方法的研究相对较多，并被相应规范所采纳[3-5]。

但如今有学者认为因为现行桥梁设计规范中预应力摩阻损失的计算公式存在一定误差，其原因是规范公式忽略了混凝土孔道弯曲受挤压产生弹性变形的影响，推导过程中未建立几何、物理方程、未给出相应的边界约束条件，认为规范公式中关于混凝土和预应力筋都是刚体假设，导致得出的公式是近似的[6]。而这种差异是否对实际工程参数较大影响，还有待进一步研究。本文采用相同条件和假设，同样选取两种常用的工程压力曲线，分别进行摩阻损失公式的推导，并与规范公式进行对比分析。

1 规范中关于摩擦引起的应力损失计算公式

为确保预应力的准确施加，避免梁体后期发生不可预见的变形，确保承载力满足设计需求，根据相应规范及设计要求在高速铁路箱梁预应力张拉前，需要对同一工地同一施工条件下的预应力摩阻相关系数进行实际测定，从而为控制锚下张拉力和预拱度设定提供可靠依据。为方便下文比较，将《混凝土结构设计规范》公式左右两端同乘以孔道横截面积A，则：

ΔP=Pcone-(μθ+kx)

(1)

式中：ΔP为计算截面处预应力筋的实际拉力(kN)；Pcon为张拉端锚下控制张拉力(kN)；θ为从张拉端至计算截面的长度上，钢筋弯起角之和(rad)；x为从张拉端至计算截面的管道长度(m)；μ为钢筋与管道壁之间的摩擦系数，按表1采用；k为考虑每米管道对其设计位置的偏差系数，按表1采用。

表1 一些常用μ、k值

2 弹性假设下摩擦引起的张拉控制力损失公式推导

在预应力混凝土构件张拉过程中，预应力筋与弯曲孔道相互作用，不仅在位置上发生相对错动，而且还会产生很大的挤压力。当两弹性体相互挤压时将发生弹性变形，接触面间的应力也将随之发生变化。在实际预应力张拉过程中预应力钢绞线与混凝土接触形式难以精确确定，为更真实地模拟二者之间的力学平衡关系，提出2种接触正压力非均匀分布的假设，即余弦分布和椭圆分布[6]。对于任意偏转角度0≤α≤π、曲率半径为R的圆弧孔道，如图1所示，取该段预应力筋为隔离体，孔道对预应力筋的法向接触压力集度表示为以θ为自变量的函数。下面分别推导出两种假设下的正压力表达式。

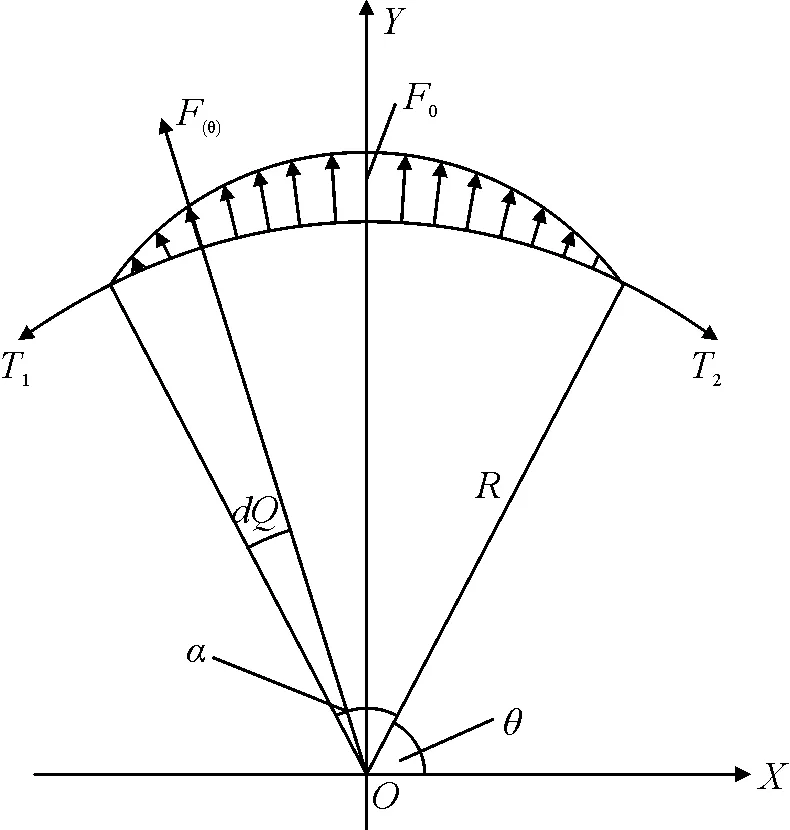
图1 弹性理论下的正压力计算

2.1 余弦压力假设下摩擦引起的张拉控制力损失公式推导

如图1所示，假设孔道内壁对预应力钢束的法向接触压力按余弦分布，压力集度用函数表示如下，其中F0为其最大值。

(2)

由静力平衡关系得：

(3)

式中：T1为张拉端，故T1>T2。进一步推导得：

(4)

(5)

所以孔道摩阻损失力为：

(6)

2.2 椭圆压力假设下摩擦引起的张拉控制力损失公式推导

如图1所示，假设孔道内壁对预应力钢束的法向接触压力按椭圆分布，则：

(7)

所以：

(8)

由静力平衡关系得：

(9)

其中，T1为张拉端，故T1>T2。

则：

(10)

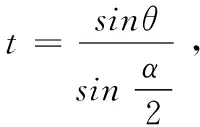
(11)

将公式(11)代入式(8)得:

(12)

所以孔道摩阻力损失为：

(13)

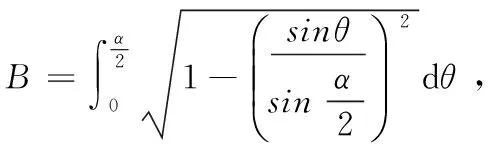
(14)

2.3 与规范摩擦引起的张拉控制力损失公式推导

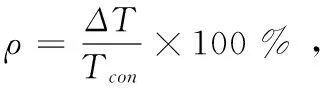
图2 μ=0.55各假设值与规范值的对比

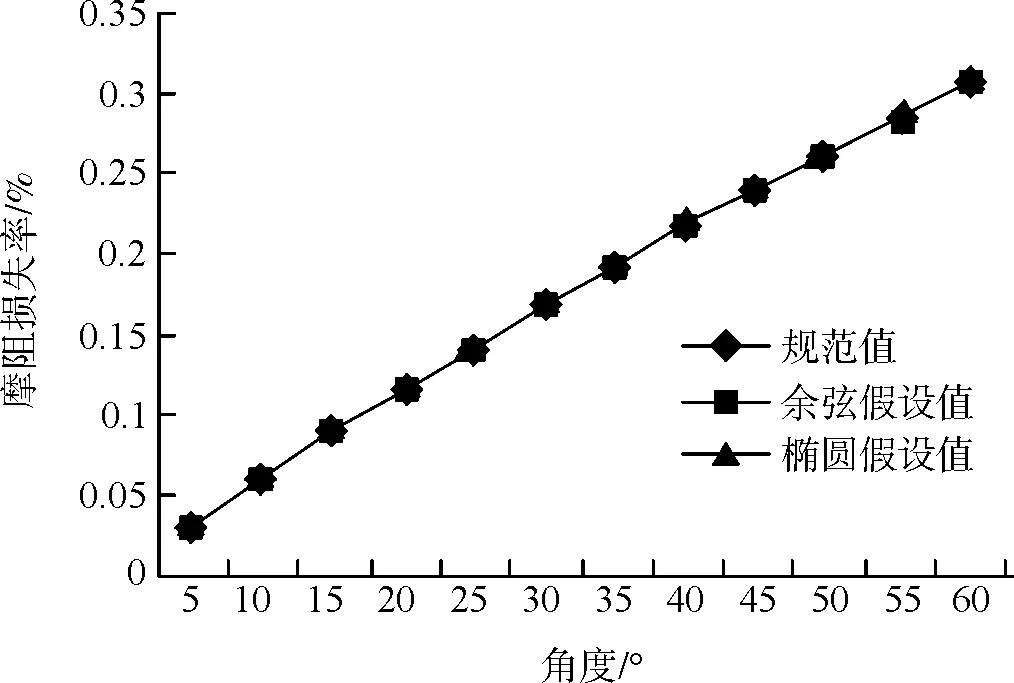
图3 μ=0.35各假设值与规范值的对比

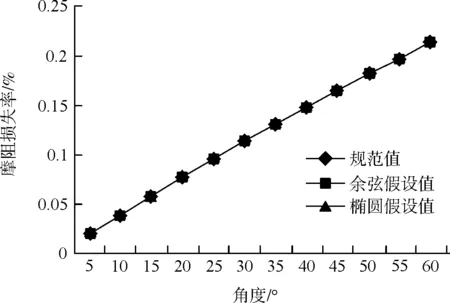
图4 μ=0.23各假设值与规范值的对比

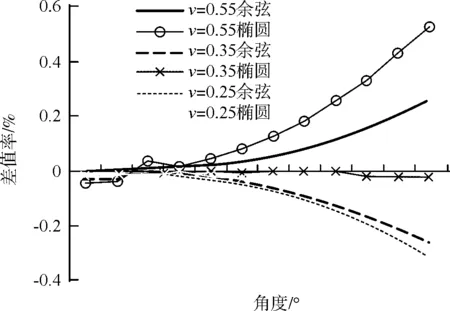
图5 规范值与假设值的差值率

由图2～图5可知：

(1)根据弹性接触理论，按余弦压力分布假设和椭圆形压力分布假设计算的预应力摩阻损失与规范公式计算出的预应力摩阻损失值基本完全相等。

(2)按余弦压力分布假设和椭圆形压力分布假设计算的预应力摩阻损失与规范公式计算出的预应力摩阻损失值只差随预应力束弯折角度的增大而有所增加，但对于常规的3种不同的成孔方式，在弯折角度60°以内的情况下，按两种不同压力分布计算出的预应力损失值与规范按等压力分布计算出的预应力损失值的误差均不超过±0.5 %，对实际工程设计施工的影响可以忽略不计。