面轨道特征的矩形排样与加工路径优化方法研究
2018-05-09周佳立
周佳立,郭 奇,吴 超,武 敏
面轨道特征的矩形排样与加工路径优化方法研究
周佳立1,郭 奇1,吴 超1,武 敏2
(1. 浙江工业大学理学院,浙江 杭州 310023;2. 浙江科技学院理学院,浙江 杭州 310023)
为了解决实际生产中遇到的一种带有面轨道特征的矩形排样问题,重点研究了自适应遗传算法和图论相结合的优化方法,极大提高了切削加工效率。该方法将路径优化问题转化为一个考察无向图连通性问题,并利用遗传算法在解空间中进行全局搜索,以寻找加工路径最优解,并按照BL定位策略完成对矩形的排样。通过对遗传算法的改进:①对初始个体基因位的合法性判断,并利用深度优先遍历结果评估个体性能的优劣;②交叉、变异算子均采用自适应机制,并且执行变异操作的对象限定为一条染色体上的断点集,极大提高了算法的性能。最后,通过实验验证了该算法在绝大多数情况下完全可以找到满足需求目标的结果,是一种非常可靠的方法。
等边矩形排样;特征加工;路径优化;自适应遗传算法
在工程应用领域中,矩形排样技术一般是指需要开料的矩形工件在给定的矩形板料上的布置和开切方式,从而达到板料利用率的最大化。上个世纪60年代,GILMORE和GOMORY[1]提出二维排样优化问题,其属于NP完全问题[2],求解难度极高,存在“组合爆炸”。对这类复杂问题,遗传算法是寻求这种满意解的最佳工具之一。遗传算法从解的串集开始搜索,覆盖面大,利于全局择优,对于组合优化中的NP问题非常有效[3]。HOPPER和TURTON[4]将改进的BL算法和遗传算法相结合,用于解决矩形的排样问题,以算例论证了算法的有效性。文献[5]提出一种将最低水平线方法与改进GA算法相结合的混合优化方法。吴忻生等[6]利用遗传算法获得矩形的排放顺序,在遗传算子操作过程中,为避免优良基因的缺失,采用了不同阶段引入不同遗传算子的方法,之后采用最低水平线法对其进行自动排样。
在数控加工中研究的问题是数控的切削加工问题。合理的切削加工路径可以避免刀具空行程,从而减少加工时间和加工成本,因此优化加工路径是提高加工效率的重要环节。
遗传算法的灵活性,使其在解决路径优化问题上同样适用,但在实际应用中,不同特征的加工零件,优化方法截然不同。文献[7]针对孔群加工路径优化模型,提出一种整数染色体的遗传算法,这种采用孔号为染色体的编码方案省去了繁杂的编解码过程,简化了遗传算法的编程。文献[8]将多轮廓加工路径优化问题转化为广义旅行商问题(generalized traveling salesman problem,GTSP),并提出了广义染色体遗传算法,该算法对多轮廓加工路径优化问题做出合理有效的解决。文献[9]根据门窗类五金配件加工中孔、槽的特殊精度要求,提出了一种基于遗传算法的热误差建模方法,在遗传算法中引入热变形补偿,进而提高了机床加工精度。
本文研究的排样与路径优化问题和上述情况截然不同,研究对象为带有面轨道特征的矩形,此类特殊的矩形排样问题,研究成果较少,排样结果不单是寻求板材的最大利用率,而且更主要考虑矩形表面轨道的整体连通性,以实现加工路径的最优化。此外,相比于传统的矩形排样问题,排样结果中单个零件的改动(旋转、替换)会对全局产生较大的扰动,一定程度上加大了研究难度。可使用图论方法中的深度优先搜索算法来解决排样图连通性。所以,本文用改进的遗传算法与图论方法求解此类特殊排样问题,最后给出了具体实例,验证该算法的可行性。
1 面轨道及其矩形排样
本文研究课题源于改进某类轨道积木的加工工艺,以提高生产效率。加工的轨道积木种类如图1所示。

图1 轨道积木种类图
由图1可知,积木的轨道种类分为内部轨道(体轨道)和表面轨道(面轨道),本文研究对象为面轨道。图2展示了所有面轨道集合的俯视图,其中基础面轨道可分为直线型基础面轨道和圆弧型基础面轨道两类,通过这两种轨道的自身组合形成直线型复合面轨道和圆弧型复合面轨道,轨道种类共5种,分别为直线轨道、十字轨道、单圆弧轨道、双圆弧轨道以及特殊的无轨平面。
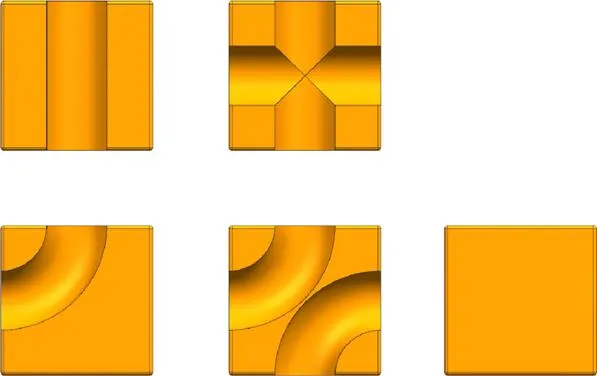
图2 面轨道示意图
如若单独加工每块积木的上表面轨道,则60块装的一套积木,其上表面加工操作要进行多达60次的装夹,多次装夹操作不但效率低下,且无法保证较高的加工精度。
本文采用组合切削加工工艺,将边长为一个单位的矩形上表面轨道在6×7的板材上进行排样,积木的上表面加工轨道可抽象为6种,如图3所示。再进行简化后,如图4所示。

图3 轨道种类

图4 简化后轨道种类
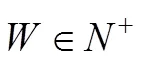
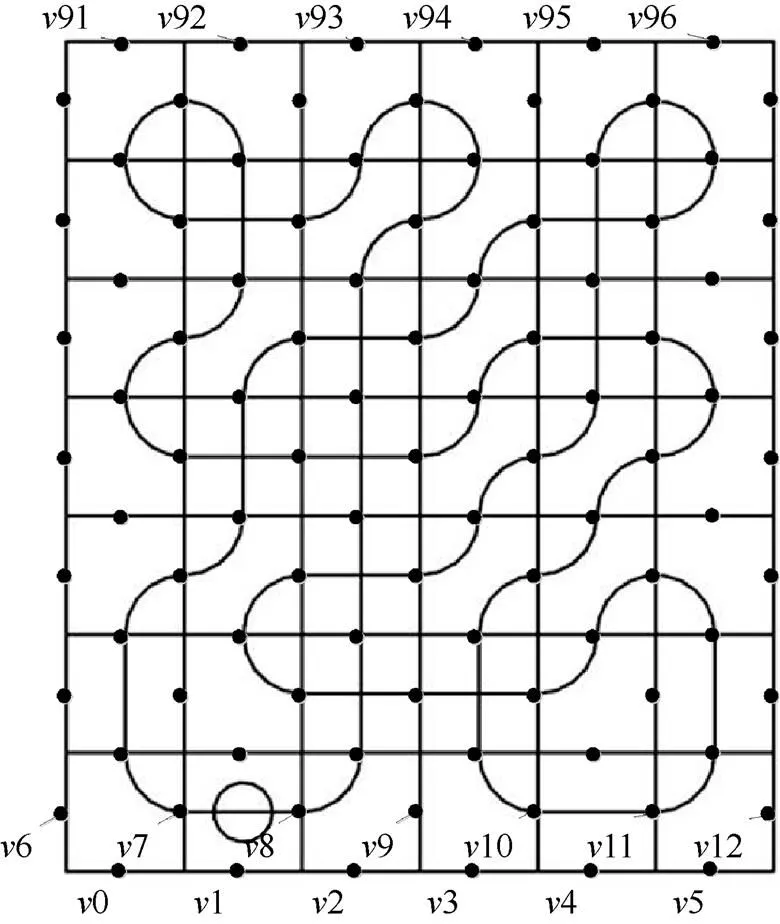
图5 排样图示例
2 面轨道加工路径优化数学模型及其求解算法
2.1 数学模型
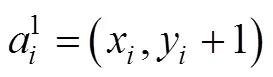
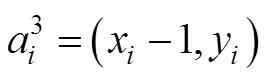
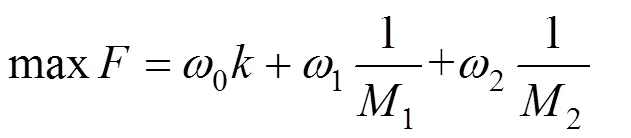
2.2 个体编码策略
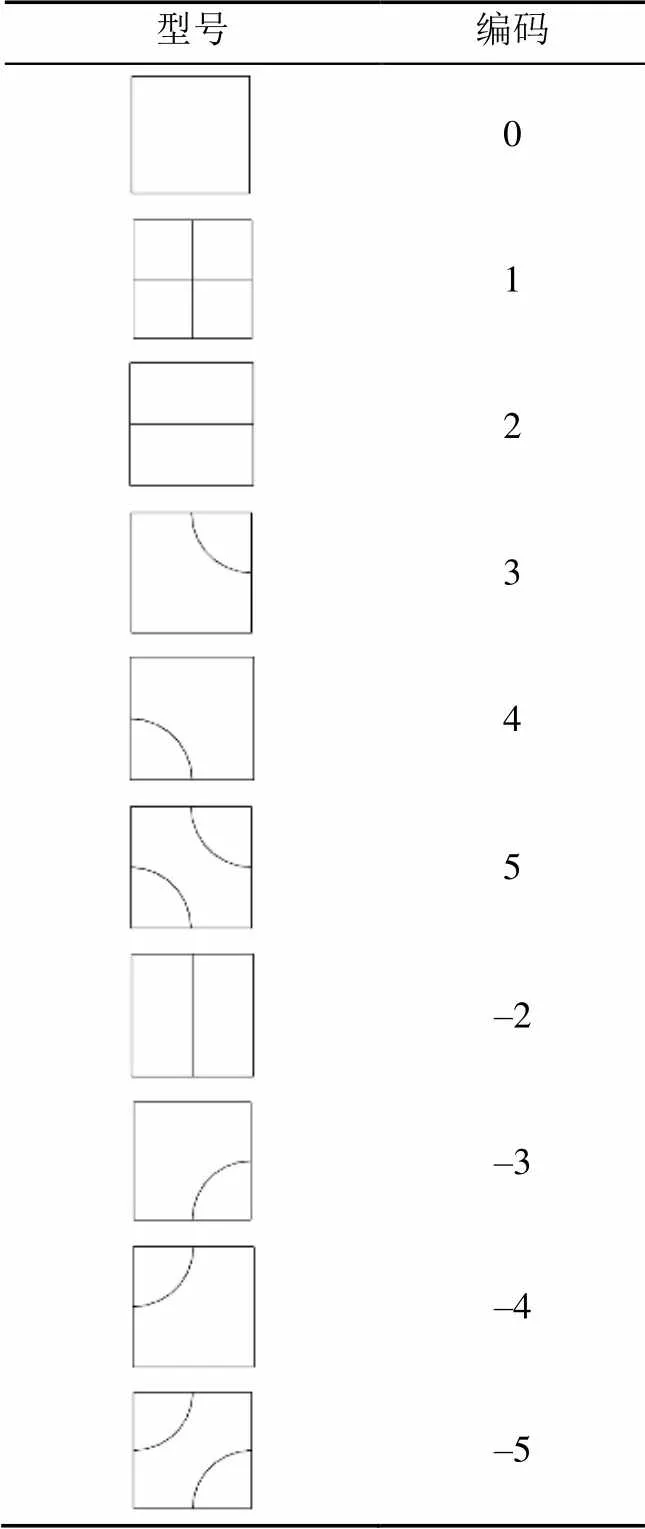
表1 矩形编码表
2.3 构造初始种群
实际加工环境如图6所示,待加工零件整齐排放在工作台,上端和右端紧贴靠山,下端及左端用工装夹钳固定在一个矩形框内,由于靠山高度高于矩形,所以在排样过程中要尽可能避免在排样图的四边出现轨道出口,如图7所示,否则会出现撞刀情况。在构造初始种群过程中,应考虑以上问题,尽量避免非法个体的产生。

图6 实际加工环境
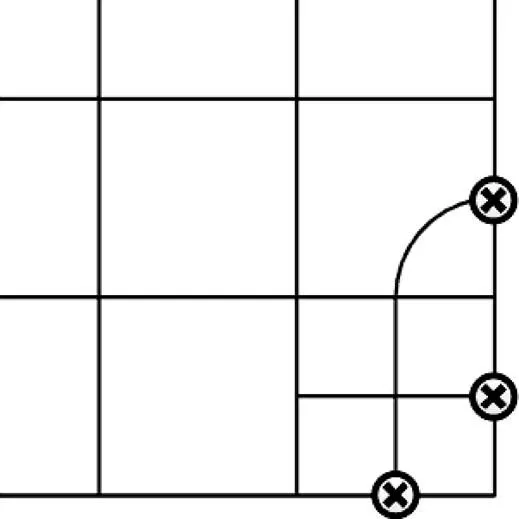
图7 排样轨道出口
产生的初始值执行如下两个操作:①以50%的概率乘以–1,这样可以产生负数序列;②按照初始值所对应排样图的位置对其进行筛选,剔除不符合加工工艺要求的非法基因,从而保证初始种群中个体的合法性,提高初始种群的质量。
2.4 个体适应度评价函数与选择算子

图8 排样图
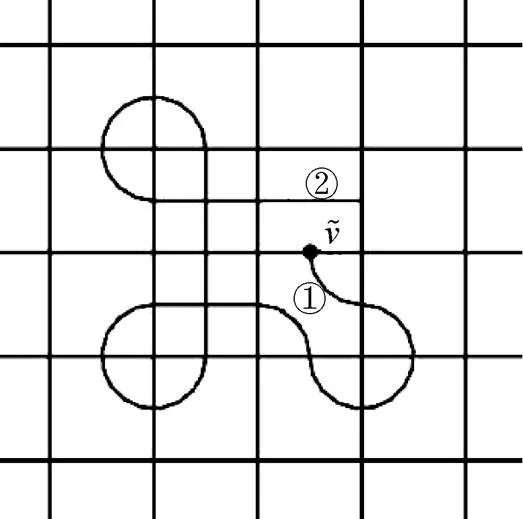
图9 排样图示例
综上所述,适应度函数取
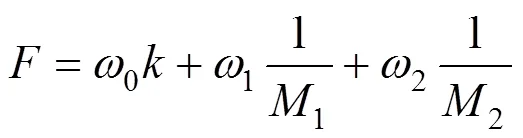
如果越大,表明个体排样布局越优。
将选择算子作用于种群,可将优良的个体直接遗传到下一代而抛弃劣质个体,体现了“适者生存”的原理,这也是遗传算法收敛性的一个重要保证条件。本文使用轮盘赌选择法和最优保存策略相结合的联合选择算子,由于轮盘赌选择法是基于概率选择的,存在统计误差,从而导致”退化”现象的发生,即优良个体失去选择机会,因此结合最优保存策略以保证当前适应度最优的个体能够进化到下一代而不被遗传操作的随机性破坏,保证算法的收敛性。具体执行过程为:
(1) 对群体中的所有个体按其适应度大小进行排序,适应度最高的10%的个体,直接遗传到下一代;
(2) 计算出每个个体被选择的概率
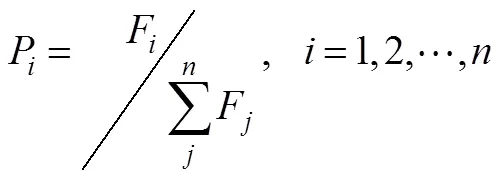
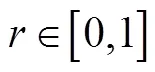
2.5 交叉和变异算子
交叉算子和变异算子是产生新个体的主要方法,前者决定了遗传算法的全局搜索能力,后者决定了遗传算法的局部搜索能力,两者相互配合,可以完成对解空间的搜索。
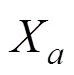
每条染色体由两层编码表示,分别为基因位和基因检索位,由于相同矩形以同一实数编码,所以在染色体执行交叉运算时,由基因检索位唯一区分同一编码号的不同基因位。
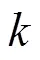
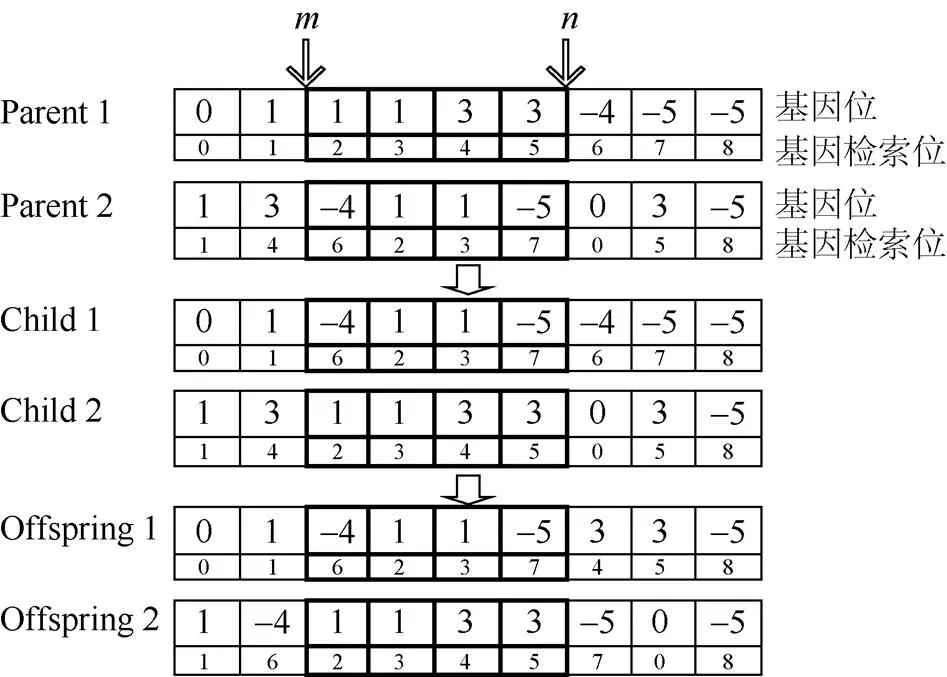
图10 个体交叉运算示意图
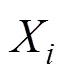
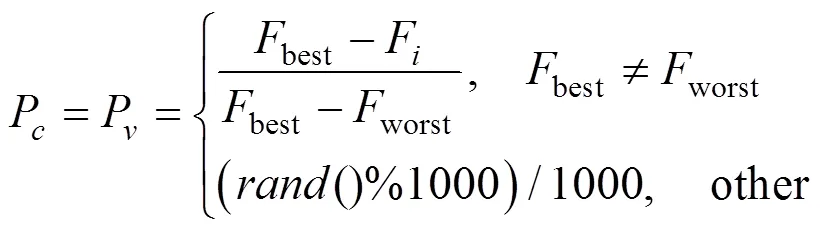
2.6 算法流程图
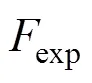
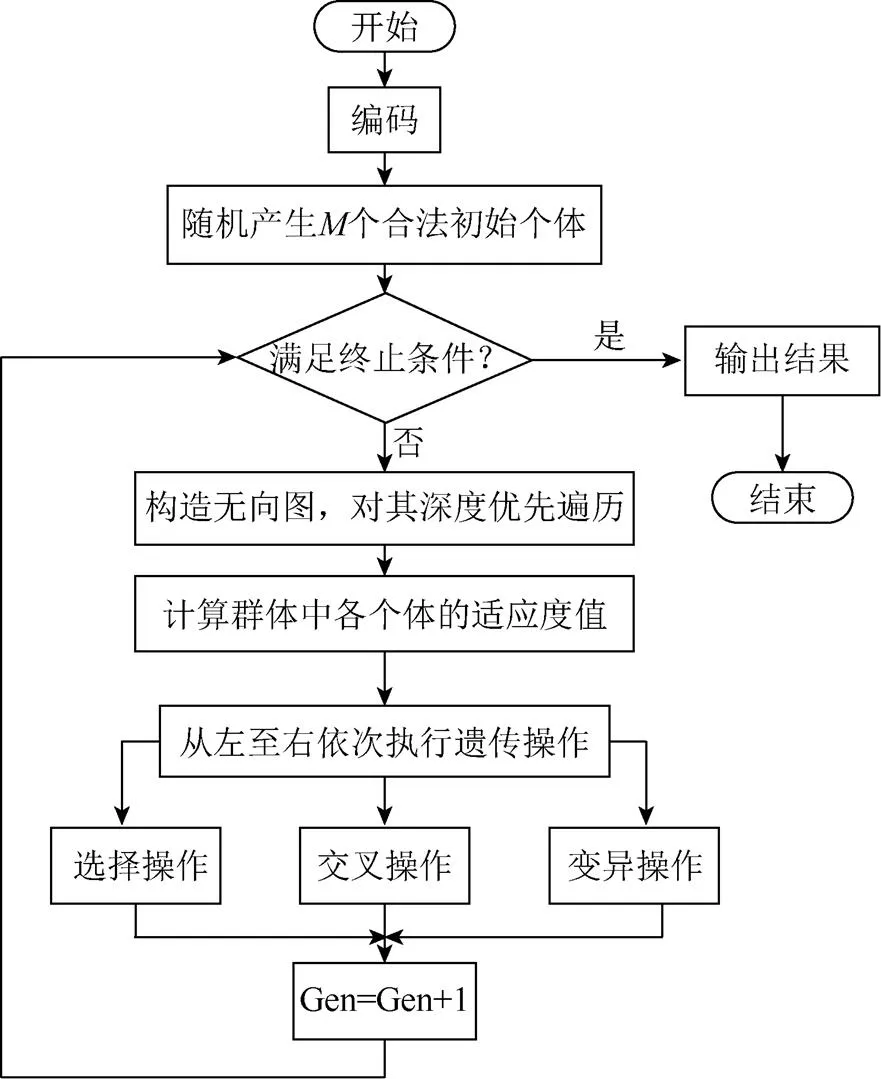
图11 算法流程图
算法实现及算例分析。
算例 1.为了验证本文中提出的特殊矩形排样算法的有效性,首先选取一组待加工矩形,待加工零件种类及个数见表2。

表2 待加工零件数目表
实验平台:普通PC机一台,处理器Inter Core i3 CPU 1.5 GHz,内存(RAM)4 GB,32位Windows 7操作系统,算法使用C++编程语言, 编译器Visual Studio 2010。
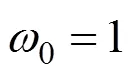
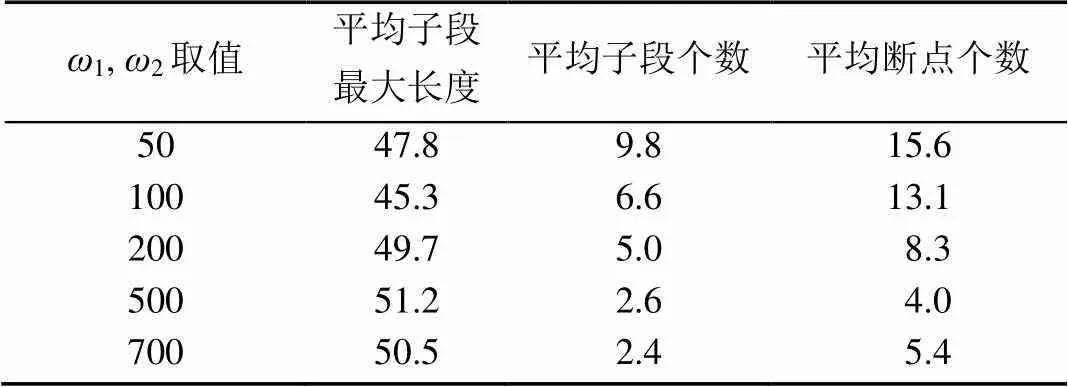
表3 试验数据表
由于遗传算法的概率性,对于同一组数据,每次运行的结果都不尽相同,所以本文采用多次运行的方法对算法的性能进行评估。由于加工零件种类的变动性,完全连通的排样图可能并不存在,所以,子段个数为3的排样图即在接受范围之内,表4为10次运行结果。
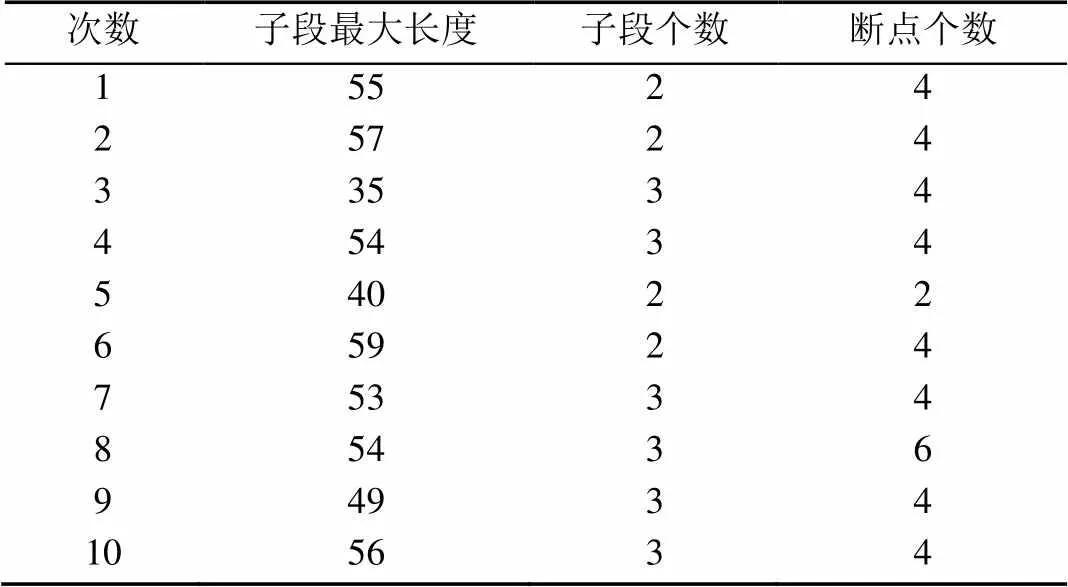
表4 试验数据表
其中所求最优排样结果的编码{3,–4,3,2,–4,–2, –3,1,5,–4,–2,–2,3,1,–5,1,5,4,–3,5,1,5,1,–4,3,–5,5,1,1,4,–3,–5,1,1,–5,–4,–3,4,–3,4,–3,4},算法在30代以后稳定,其收敛过程如图12所示。分别为第2代、第11代、第20代和第30代的排样情况。

图12 排样情况
算例 2. 选取3组不同代加工矩形,应用该算法求解最优排样图,以说明该算法针对此类问题具有普遍的适用性。试验平台、运行参数均不改变,采用每组代加工矩形运行十次取平均值的方法考察排样结果。表5为每组矩形的组合情况及运行结果,其中,运行结果主要由平均子段最大长度、平均子段个数和平均断点个数来评估。
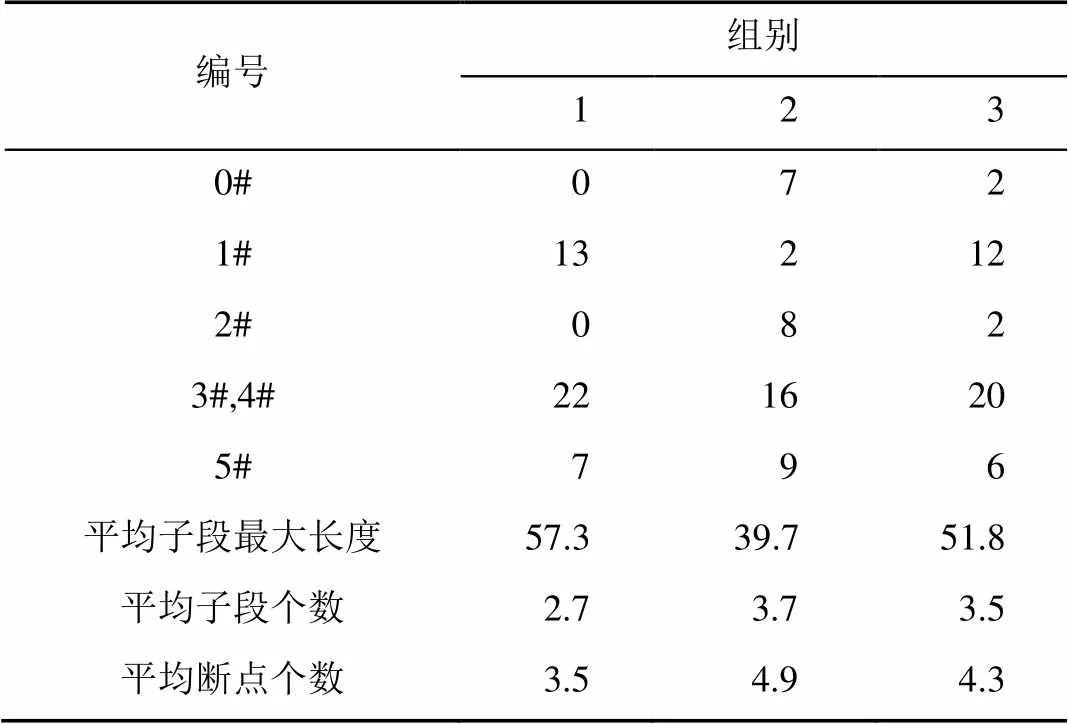
表5 排样结果评估
由表5可知,组2中0号积木数量较多,平均子段长度明显下降,这是因为无轨积木占用了母版多数空间,轨道长度自然缩减,这也是符合常理的。平均子段个数在3个左右,也在本文的接受范围之内。所以,该算法可以有效解决此类特殊矩形排样问题。
3 结束语
本文将一种改进的遗传算法和图论方法相结合,主要研究方向为一种带有面轨道特征的矩形排样问题,并以路径最优为目标,最终将路径优化问题转化为图论连通性问题,实现了矩形在母板上的合理排样。在遗传算法中,通过对初始个体基因位的合法性判断,有效提高了初始种群的质量,交叉、变异算子均采用自适应机制,并且执行变异操作的对象限定为一条染色体上的断点集,增强了算法的局部搜索能力,最后将排样结果转化为无向图,通过计算无向图的连通程度来衡量个体的优良性。
对于矩形排样问题,任何算法也难以保证得到最优解,所以在具体应用问题上,需多次试验以寻得最优排样效果。图13为实际生产中的应用实例,极大提高了生产效率。

图13 实际生产应用实例
[1] GILMORE P C, GOMORY R E. Multistage cutting stock problems of two and more dimensions [J]. Operations Research, 1965, 13(1): 94-120.
[2] JINDAL P, KUMAR A. Towers the solution of NP complete problems [J]. Jouranl of Applied Computer Science & Mathematics, 2010, 4(9): 63-65.
[3] 贾志欣. 排样问题的研究现状与趋势[J]. 计算机辅助设计与图形学学报, 2004, 17(7): 890-893.
[4] HOPPER E, TURTON B C. An empirical investigation of meta-heuristic and heuristic algorithms for a 2D packing problem [J]. European Journal of Operational Research, 2001, 128(1): 34-57.
[5] LIU H M, ZHOU J, WU X S, et al. Optimization algorithm for rectangle packing problem based on varied-factor genetic algorithm and lowest front-line strategy [C]//2014 IEEE Congress on Evolutionary Computation (CEC). New York: IEEE Press, 2014: 352-357.
[6] 吴忻生, 吴超成, 刘海明. 基于改进遗传算法的矩形排样优化算法[J]. 制造业自动化, 2013, 35(10): 55-58.
[7] 肖军民. 一种改进遗传算法在孔群加工路径中的优化[J]. 组合机床与自动化加工技术, 2015(2): 151-153.
[8] HUANG H, YANG X, HAO Z, et al. Hybrid chromosome genetic algorithm for generalized traveling salesman problems [C]//International Conference on Advances in Natural Computation. Berlin: Springer Press, 2005: 137-140.
[9] XIAO J, YAN M. Heat error modeling methods of NC machine tool machining holes or slots of door hardware based on genetic algorithms [C]//Proceedings of 2011 International Conference on Electronic & Machanical Engineering and Information Technology. New York: IEEE Press, 2011: 3326-3329.
[10] 杨卫波, 王万良, 张景玲, 等. 基于模拟退火算法的矩形优化排样[J]. 计算机工程与应用, 2016, 52(7): 259-263.
Research on Packing Problem and Cutting Path Optimization of Rectangle with Surface Orbit Characteristics
ZHOU Jiali1, GUO Qi1, WU Chao1, WU Min2
(1. College of Science, Zhejiang University of Technology, Hangzhou Zhejing 310023, China;2. College of Scienc, Zhejiang University of Science and Technology, Hangzhou Zhejing 310023, China)
The purpose of this paper is to solve the equilateral rectangular packing problem characterized by surface orbit arised in practical production. We focus on the optimization system based on adaptive genetic algorithm and graph theory, and greatly improve the cutting efficiency. Our method target the optimization of the machining path, in this method, the path optimization problem is turned into an undirected graph connectivity problem, and using genetic algorithm to find the optimized machining path. The optimal solution of the final search is used to arrange the rectangular parts according to BL positioning strategy. Through the improvement of genetic algorithm, such as: ① the judgment of the legitimacy of the initial individual genes, and using the depth first traversal results evaluation of individual performance. ② The crossover and mutation operators use adaptive mechanism, and the object that performs the mutation operation is limited to a broken point set on a chromosome, which greatly improves the performance of the algorithm. Finally, the experiments show that the algorithm can provide the available solution in most cases, and it is also a very reliable method.
equilateral rectangle packing; feature machining; path optimization; adaptive genetic algorithm
TP 391
10.11996/JG.j.2095-302X.2018020256
A
2095-302X(2018)02-0256-07
2017-07-04;
2017-08-05
青年科学基金项目(11301482);科技型中小企业技术创新基金项目(13C26213302261);浙江省重大科技专项项目(2013C01077);浙江省科技厅面上项目(2015F50021)
周佳立(1981-),男,浙江诸暨人,副教授,博士,硕士生导师。主要研究方向为计算机视觉、模式识别、机器人切削。 E-mail:zhoulue@zjut.edu.cn
