六角网格同构模型的建模及其应用
2018-05-08雷洋
雷洋
摘要 本文主要分析了六角网格同构模型的建模及其应用涉及六角网格的绘制,特别涉及平面六角网格中的一种同构模型,以及基于该同构模型构建的六角网格上进行的兵棋地图信息存储、获取的结构和应用算法,适用于兵棋推演系统中兵棋地图的相关应用,仅供参考。
【关键词】六角网格 同构模型 建模及应用
1 背景技术
在目前,一般六角网格的应用过程中,由于不需要进行与六角网格相关联的数据存储与信息识别,因而采用较为传统的绘制方式,导致绘制过程中的重复,在此基础上进行的数据存储必将产生冗余、信息获取效率降低,影响用户的使用时间和流畅度,不能经济运行,浪费了资源。
2 技术实现目的和意义
目的在于针对上述不足提供一种六角网格同构模型的建模及应用,该六角网格同构模型是一种结构简单、高效率的,能够在六角网格下进行信息存储和信息获取的模型。
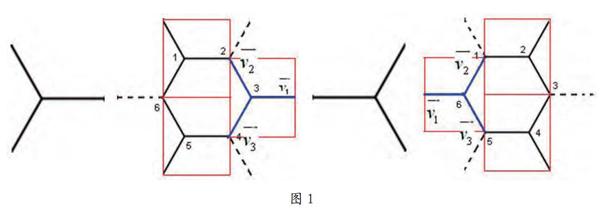
相关技术采取以下技术方案实现的:六角网格同构模型为六角格,其基元为一点三线图形,三条线段集中交汇于一点,水平方向线段为1号线v1,水平方向线段上部相邻的线段为2号线V,水平方向线段下部相邻的线段为3号线V3,三条线段两两之间的角度相同,均为120度。基于该形状定义的计算机化的基本数据结构+六角格、边、两侧的识别算法。
3 六角网格同构模型的建模分析
六角网格同构模型的建模包括如下步骤:
(l)确定使用的六角网格同构模型,六角网格同构模型具有两种基元,任意一种都能够构建出六角网格。
(2)在步骤1中所选取的六角网格同构模型中,取三线交汇点为基本点,两个六角网格同构模型拼接而交会的点称为扩展点,六角网格同构模型三条边两两之间的角度均为120度,因此基本点的坐标信息即可确定同构模型的位置。
(3)确定进行六角网格化的电子地图区域、六角格的大小信息:根据步骤2中确定的每一个六角网格同构模型基本点的位置信息,在电子化地图区域内建立同构模型的二维平面区域与地图区域的对应关系,该关系可抽象为一个矩阵,将矩阵的坐标作为六角网格同构模型的唯一标示。
图1是本发明同构模型的平面结构及其在六角网格中的表现形式示意图。
(4)将六角网格同构模型与六角网格中的单独六角格一一对应,在步骤3所述矩阵关系的平面中,通过计算地图平面上任何一点与地图边界、同构模型基本点之间的平面线性关系,确定该点与六角格、六角格边之间的关系,从而完成建模。
在步骤4中所述的对应时间效率如下:
其中T(n)表示识别所消耗的时间,f(n)是算法的函数表达式,n表示矩阵规模。
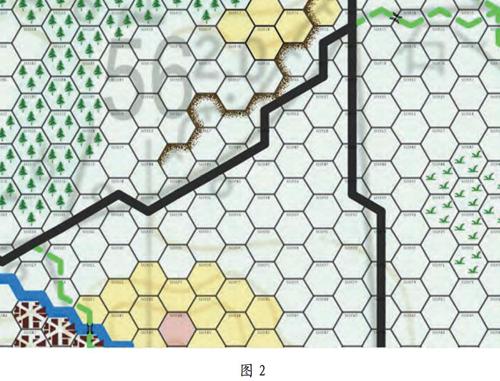
图2基于六角网格同构模型应用在兵棋六角格化电子地图中的部分内容示意图。
六角网格同构模型在兵棋六角格化电子地图的应用过程中,通常将六角格内地图信息抽象化,并与六角格、六角格边、六角格两侧建立对应关系。基于步骤4中定位方法,可以快速存储、获取各种地图信息。基于同构模型的兵棋地图信息相关存储结构,存储、获取算法以及扩展应用算法。
4 结语
通过分析六角网格的结构特点,得到六角网格中的同构形状,并在此基础上建立信息存储结构,六角网格的同构模型在六角网格中具有唯一性,通过同构模型的实例可以无缝拼接任意的六角网格,同时具有六角格、六角格边、六角格顶点的不重复性。在此特点上进行的识别算法、数据存储、拓展应用具有良好的基础。通过几何学和微分学的分析,实现六角格、六角格边缘、六角格边缘两侧的快速识别算法,构建六角网格内基于上述内容的同构模型。与此同时,将该同构模型应用于兵棋推演系统的兵棋地图中,实现各种地图信息的快速存储、检索算法,以及兵棋地圖中的通视算法。该同构模型为建立基于六角网格的兵棋地图其它功能奠定了高效的应用基础。
