CEEMD-WT和CNN在短期风速预测中的应用研究

颜宏文，卢格宇

YAN Hongwen,LU Geyu

长沙理工大学 计算机与通信工程学院，长沙 410114

School of Computer&Communication Engineering,Changsha University of Science&Technology,Changsha 410114,China

CNKI网络出版：2017-07-06,http://kns.cnki.net/kcms/detail/11.2127.TP.20170706.0758.002.html

1 引言

目前，风能作为一种清洁、有利于生态环境的可再生能源[1]，已经受到越来越多国家的重视。然而，风速具有随机性、不稳定性和非线性的特征[2]，这些会对风力发电的电力系统造成一定的影响，为了确保电力系统的安全性，需要对风速进行短期的预测来提前做好相应的应对措施。

近些年来，国内外的学者研究出了大量的风速预测模型。到目前为止，主要有物理方法、统计方法和混合模型三种方法[3-4]。物理模型使用物理因素来估计未来的风速[5]，其中数值天气预报模型（Numerical Weather Prediction，NWP）是所有物理模型中最常用的一种。统计方法主要通过历史数据来构建模型。有四种传统的统计模型：自回归模型（Autoregressive Model，AR）、移动平均模型（Moving Average Model，MA）、自回归移动平均模型（Autoregressive Moving Average Model，ARMA）[6]和自回归整合移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）[7]。由于物理模型和统计模型的局限性，一些混合模型被提出，研究表明，混合模型预测比单个预测模型会有更好的预测结果[8]。最常见的有两种混合策略，一种策略是混合信号分解算法和机器学习算法，通过信号分解算法把风速序列分解成一系列的稳定分量，然后通过机器学习算法例如神经网络、支持向量机等对每个分量分别进行预测，最后把预测的结果重构起来得到最终的预测结果，Wang等[9]提出了经验模态分解（Empirical Mode Decomposition，EMD）和简单递归神经网络（Elman Neural Network，ENN）的混合预测模型，该模型思想为EMD分解算法把原始的风速数据集分解成一系列的固有模态分量，然后利用ENN神经网络训练每个固有模态分量；另一种策略是混合智能优化算法和机器学习算法，通过智能优化算法优化机器学习算法的参数，然后通过优化后的机器学习算法进行预测，其中常利用到的智能优化算法包括遗传算法、进化算法、粒子群算法和模拟退火算法等，基于此种策略，Jiang等[10]提出了模拟退火算法（Simulated Annealing，SA）和BP神经网络的混合预测模型，该模型思想为通过SA算法优化BP神经网络的训练参数来提高BP神经网络的预测性能。

本文基于混合信号分解算法与机器学习算法的混合策略提出了基于CEEMD-WT和卷积神经网络的混合预测模型。CEEMD信号分解算法相比于其他的信号分解算法能更好地解决模态混叠问题，WT算法主要用来对CEEMD信号分解后的固有模态分量进行二次去噪，卷积神经网络包含多层感知器并且能得到更加细节具体的特征。与传统的神经网络只对单一的风速序列进行训练不同的是，通过卷积神经网络可以学习出风速对应的温度、当地气压、海平面气压、风向和风切变的属性特征。实验表明，该模型能大大降低预测风速的误差。

2 理论基础

2.1 卷积神经网络

卷积神经网络是一种深度学习方法，近年来在模式识别、图像分类[11]方面有着重要的应用。它的整体结构由卷积层、子样本层以及全连接层组成，其训练流程如图1所示。

在卷积层中，先前的层的特征映射与卷积核进行卷积计算并且通过激励函数生成输出的特征映射。每个输出的特征映射可能组合了多个输入特征映射的卷积。通常，卷积计算有如下公式：

其中，Mj表示选择的输入特征映射；每个输出特征映射会加上一个偏置参数b；∗号表示卷积核k在l-1层卷积层上与所有相关联的特征映射作卷积运算；激励函数 f(⋅)则取Sigmoid函数。

图1 卷积神经网络训练流程

在子样本层中，其输入特征来自于上一层的输出特征，并从中提取局部特征。子样本层的局部特征提取如下式：

其中，down(⋅)表示子取样函数，本文采用的操作是取特征值的平均值；表示该层的输出特征映射；激励函数f(⋅)与卷积层相同，取Sigmoid函数；表示该层的输入特征映射，即上一层的输出特征映射；子取样函数会乘上一个偏置参数β；每个输出特征映射会加上一个偏置参数b。

全接连层是卷积神经网络的最后一层，把多个卷积层和子样本层卷积计算得到的特征映射作为全连接层的输入特征，经过全接连层的计算得到最终的输出向量。全接连层计算如下式：

其中，xl表示最终的输出向量；f(⋅)取Sigmoid函数；Kl表示第l-1层与第l层的权重；每个输出加上总的偏置参数b得到最终的输出向量。

2.2 CEEMD算法

完备总体经验模态分解（Complete Ensemble Empirical Mode Decomposition，CEEMD）是经验模态分解（EMD）算法的改进算法。EMD算法[12]是一种分析非线性和非平稳序列的方法。该算法能把一个序列分解成一系列不同频率的子序列称之为固有模态函数（Intrinsic Mode Function，IMF）。然而，EMD算法存在模态混叠的缺点[13]，模态混叠会影响分解的固有模态函数的精确度。

为了减轻模态混叠带来的影响，Torres等[14]提出了CEEMD方法。CEEMD算法是一种噪声辅助方法。在CEEMD算法中，分解的模态表示为～，于是可以计算第一个唯一的残差为：

其中，x(t)表示原始信号；给x(t)加上i组高斯白噪声信号后，分别应用EMD算法分解这些信号可以得到它们模态IMF，对这i个模态进行加总平均可以得到CEEMD算法的第一个固有模态函数；然后，对r1(t)添加不同实现的噪声并进行与上述相同的操作可以得到CEEMD算法的第二个固有模态函数，则下一个残差为r2(t)，计算；最后对剩余模态继续上述操作直到满足条件时结束，可以得到最后分解的固有模态分量和残差。

2.3 WT算法

小波变换（WT）是一种常用的信号分析方法，特别是在时域和频域上有较好的分析能力。近些年来，由于其优秀的去噪效果，在非线性、非稳定的时间序列去噪方面有较多的应用[15]。

利用小波变换去噪声方法的步骤如下：

（1）已知数据集 y=y1,y2,…,yN，其中N=2J并且J∈Z，则通过离散小波变换计算小波系数wjk(y)为：

（2）对每个数量级 j=m,…,J-1估计它们的噪声方差为：

其中med(⋅)表示求中位数。

（3）计算每个数量级 j的阈值Tj为：

（4）对于 k=1,2,…,2j，软阈值估计为：

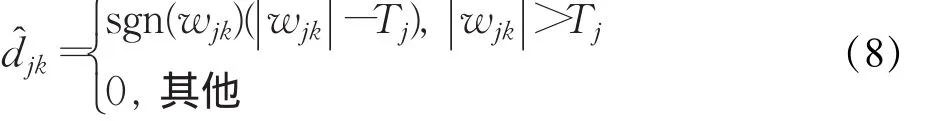
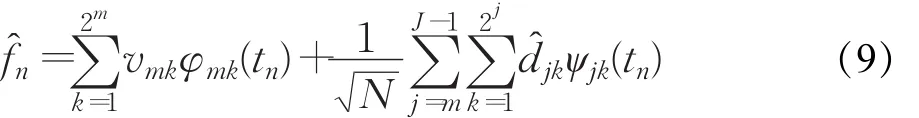
3 本文提出的模型

3.1 模型描述

由于风速序列具有非线性，不稳定的特点，直接把原始风速序列作为输入会使最后的风速预测结果误差比较大。针对以上的问题，本文拟采用完备总体经验模态分解（CEEMD）先把原始风速序列分解成一系列的相对稳定、平稳的固有模态函数和一个残差；然后利用小波变换（WT）对每个固有模态函数进行二次去噪；接着把二次去噪后的固有模态函数、残差和相对应时刻的温度、当地气压、海平面气压、风向和风切变作为卷积神经网络的输入，对它们进行训练，得到每个固有模态函数和残差的预测量；最后重构这些固有模态函数和残差预测量可以得到最后的预测结果。该模型的流程如图2所示。

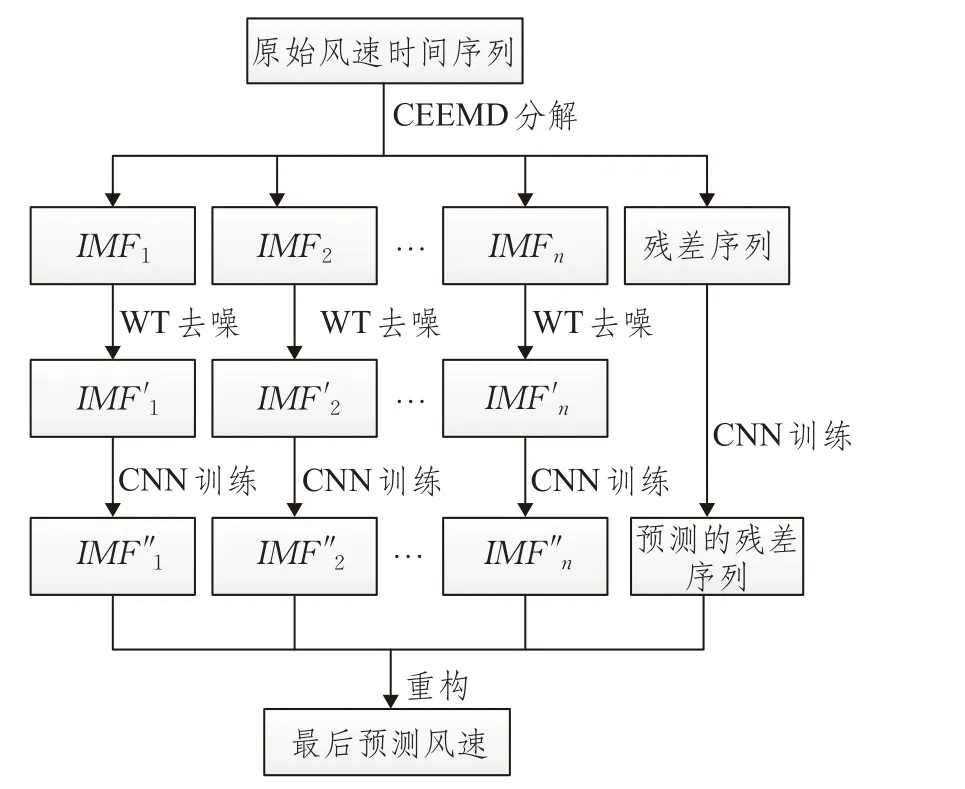
图2 风速预测流程图

从图2可以看出IMF1,IMF2,…,IMFn表示CEEMD算法分解的n个固有模态函数表示用小波二次去噪后的固有模态函数表示经过卷积神经网络训练后预测的固有模态函数。最后重构n个IMF''和预测的残差序列可以得到最终的预测结果。

3.2 考虑属性特征的卷积神经网络

为了训练出更准确的风速特征，本文利用卷积神经网络的输入数据为二维的特点，把包括风速、温度、当地气压、海平面气压、风向和风切变这6个属性的风速记录作为输入。各属性说明如表1所示。

表1 风速记录属性说明

本文中，由于每个去噪后的固有模态函数是一个向量，假设一个固有模态函数有m个数据，加上上述风速在对应时刻的5个属性，可知卷积神经网络的输入层有6×m个神经元，那么输入数据即为6×m的矩阵。设置第一层卷积层有6个特征映射，其中第1个特征映射有1×(m-p+1)个神经元，该特征映射表示输入风速的特征映射，其中 p表示接受域的宽度，接受域的长度为1，则1×p表示接受域的大小；其他5个特征映射中的每个映射分别有4×(m-p+1)个神经元，这5个特征映射分别表示输入属性温度、当地气压、海平面气压、风向和风切变中任意4个属性的特征映射；于是第一层子样本层有6个特征映射，第1个特征映射有1×[(m-p+1)/2]个神经元，其余5个特征映射有4×[(m-p+1)/2]个神经元；然后进行第二次卷积和第二次子取样，第二次卷积层有21个特征映射，每个特征映射有1×[(m-p+1)/2-p+1]个神经元，第二次子样本层有1×[(m-p+1)/2-p+1]/2个神经元，分布在21个特征映射上；最后，通过全连接层处理可以输出m′个预测数据。根据图1以及上述说明，本文的卷积神经网络训练流程如图3所示。

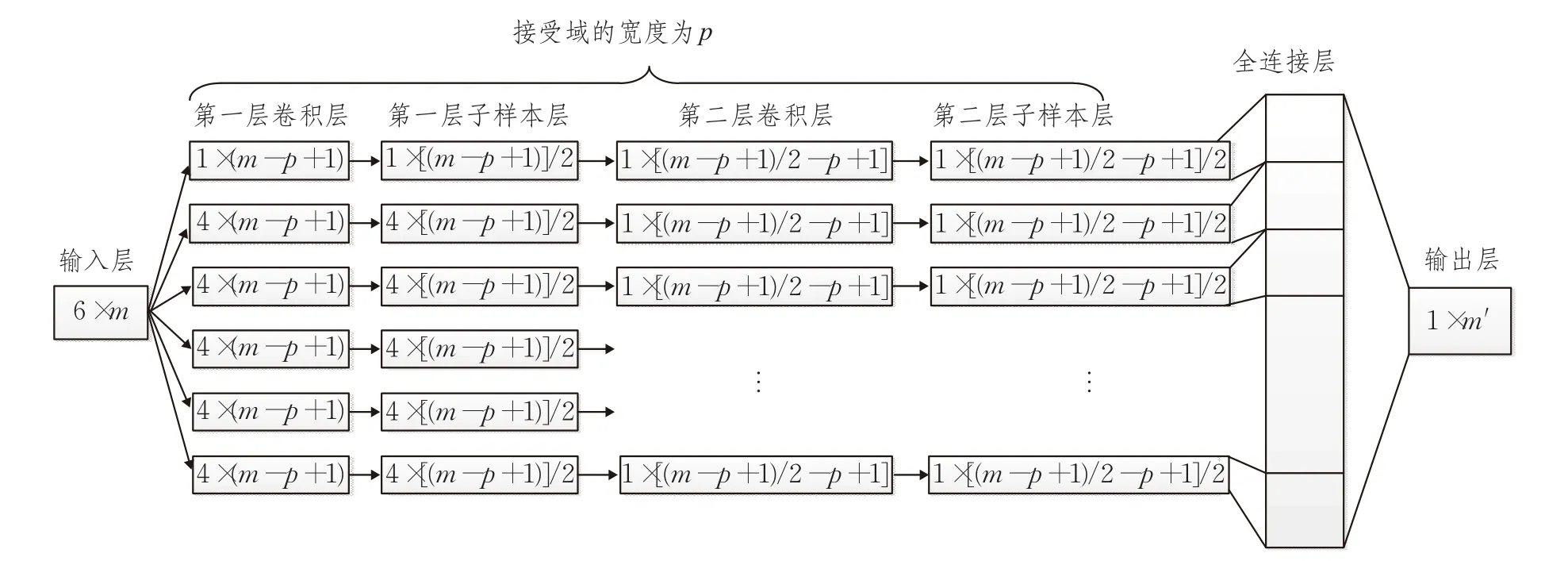
图3 本文卷积神经网络训练流程

3.3 本模型卷积神经网络训练步骤

根据2.1节和3.2节，可以总结出适应本模型的卷积神经网络的训练步骤如下：

（1）从风速数据集中取一个样本集(X,Yp)，X表示输入的风速记录，Yp表示真实的输出风速。

（2）初始化卷积神经网络的参数：第一层卷积层的特征映射数量，接收域的大小，第一层子样本层的特征映射数量，第二层卷积层的特征映射数量，第二层子样本层的特征映射数量。

（3）利用式（1）对第一层卷积层中的风速和其他属性分别进行特征提取。

（4）利用式（2）对第一层子样本层进行局部特征映射。

（5）第二层卷积层进行第二次卷积。

（6）第二层子样本层与步骤（4）相同进行局部特征映射。

（7）全连接层利用式（3）计算出输出向量Op。

（8）计算真实的输出Yp与实际的输出Op的差值。

（9）根据梯度下降法，反向传播调整权重。

（10）判断迭代是否结束，如果结束则输出最终的预测值；否则，回到步骤（3）继续训练。

3.4 本模型预测的具体步骤

输入：m个数据的风速序列s[τ]及τ时刻对应的温度序列 t[τ]、当地气压序列 p[τ]、海平面气压序列sp[τ]、风向序列 d[τ]和风切变序列 sh[τ]。

输出：m′个预测数据的风速序列s[τ′]。

步骤1应用2.2节中的CEEMD算法对s[τ]进行分解，分解后得到n个固有模态函数分别为 IMF1[τ]，IMF2[τ]，…，IMFn[τ]和一个残差序列 r[τ]。其中，这 n个固有模态分量和残差序列r[τ]都为1×m的向量。

步骤2应用2.3节中的WT算法对步骤1得到的n个固有模态函数分别进行二次去噪，得到二次去噪后的固有模态函数

步骤3对步骤2经过二次去噪处理后得到的n个固有模态函数和步骤1中得到的残差序列r[τ]分别与t[τ]、p[τ]、sp[τ]、d[τ]和 sh[τ]作为卷积神经网络的输入。

步骤4根据3.3节中卷积神经网络的训练步骤对步骤3的输入进行训练。设置卷积神经网络的参数：第一层卷积层的特征映射数量为6，接收域的大小为1×p，第一层子样本层的特征映射数量为6，第二层卷积层的特征映射数量为21，第二层子样本层的特征映射数量为21。

步骤5重复步骤4共n+1次，得到n个固有模态分量的预测值和一个残差序列的预测值，分别为。其中，它们都为1×m′的向量。

该组患者接受阿司匹林（国药准字J20130078；拜耳医药保健有限公司生产）治疗方案，初次及次日服用剂量为300 mg，从第3 d开始调整服用剂量，100 mg/次，1次/d。

步骤6把步骤5中得到的结果全部重构得到最终的预测结果 s[τ′]。

4 实验结果分析

4.1 实验数据准备

实验采用的数据集取自位于科罗拉多山脉的美国国家风速观测站（http：//www.nrel.gov/midc/nwtc_m2）。本文选取2014年8月1日一共1 440条风速数据，每一分钟取一次平均风速，并且以1 296条数据作为训练数据集，以后144条数据作为测试数据集。在数据集中，每条风速记录包括风速、温度、当地气压、海平面气压、风向和风切变6个属性。部分风速记录数据如表2所示。

表2 部分风速记录

采用MATLAB对本文提出的模型进行风速预测实验，并把本文提出的模型分别与单一CNN预测模型、文献[7]中提出的ARIMA预测模型、文献[9]中提出的EMD-ENN预测模型和文献[10]中提出的SA-BP预测模型相比较。比较的指标用绝对平均误差（Mean Absolute Error，MAE）、绝对平均百分比误差（Mean Absolute Percentage Error，MAPE）和均方根误差（Root Mean Square Error，RMSE）表示，它们的计算方法如式（10）～（12）所示。

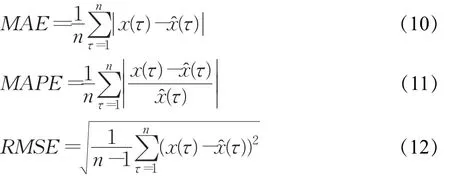
其中，x(τ)表示原始风速序列，xˆ(τ)表示预测的风速序列。

4.2 模型实验结果

首先对风速训练数据集进行CEEMD分解和小波二次去噪，能得到10个固有模态函数和1个残差序列，如图4（a）～（k）所示。

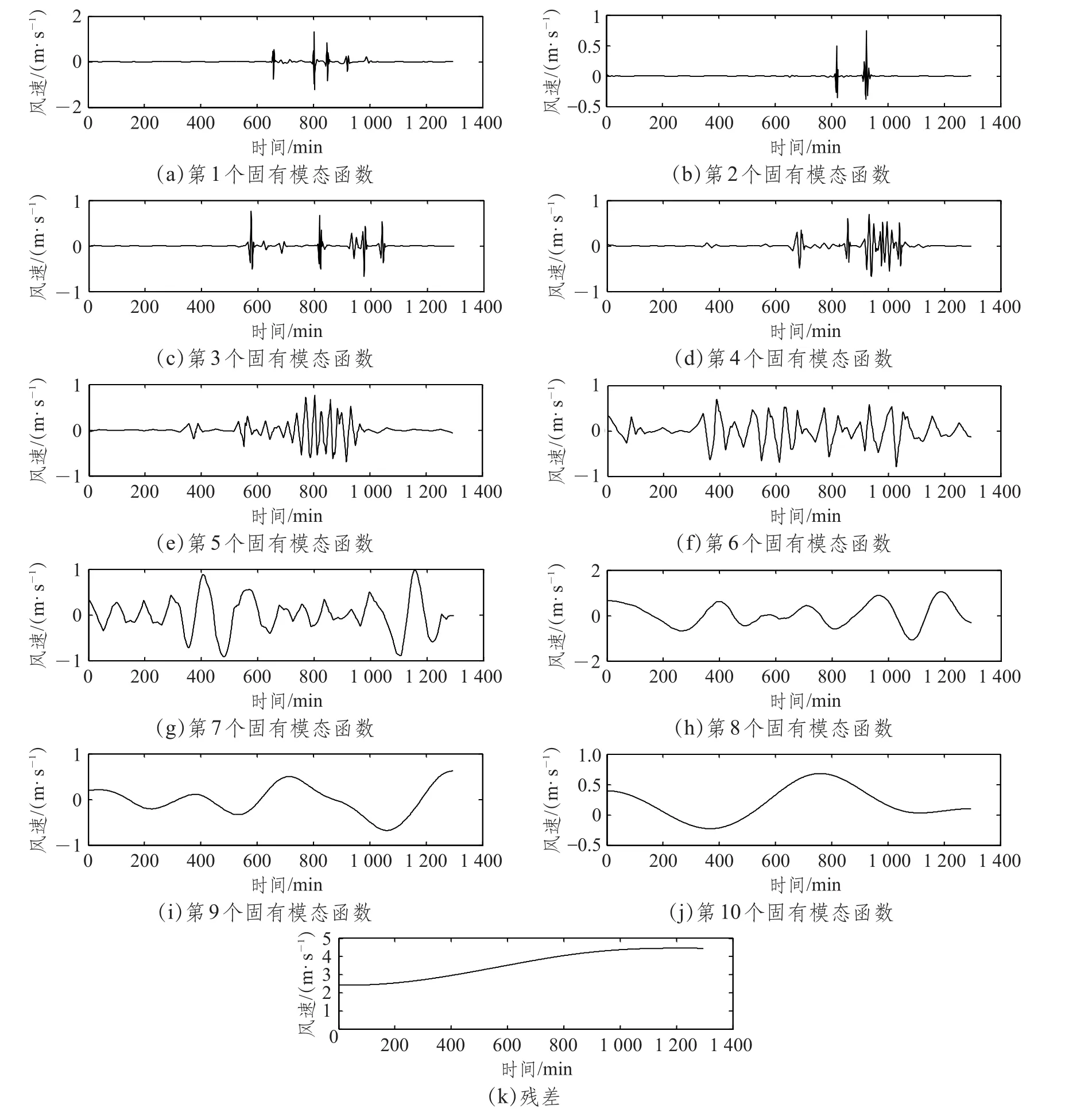
图4 CEEMD分解后和小波二次去噪后的10个固有模态函数

然后利用式（9）对图4中的固有模态函数和残差进行重构，得到重构的风速序列，重构的风速序列与原始风速序列的比较如图5所示。

图5 重构序列与原始序列

从图5可以看出重构的风速序列保留了原始序列的绝大部分的特征，消除了一些陡峭的极值，极大地增强了序列的稳定性，这表明CEEMD算法的分解和WT算法的二次去噪效果是非常理想的。最后，对图4中的每个固有模态函数和残差分别加上3.2节中提到的5个属性进行卷积神经网络训练预测，根据3.2节及图3，设置本文模型中卷积神经网络的训练参数如表3所示。

表3 卷积神经网络训练参数设置

得到预测的结果后，对预测的固有模态函数和残差进行重构能得到最后的预测结果，如图6所示。根据式（10）～（12）可以计算出风速预测的 MAPE、MAE 和RMSE分别为2.484%、0.082 m/s和0.106 m/s。

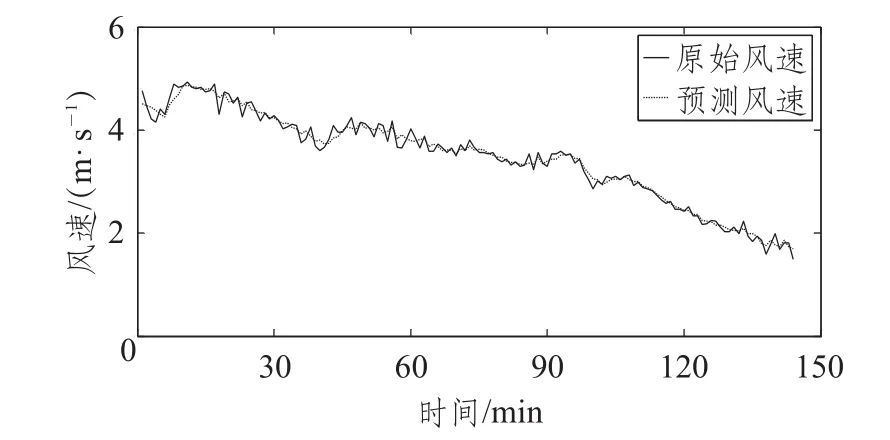
图6 本文提出的模型预测风速与原始风速

4.3 不同模型实验结果比较

对ARIMA预测模型、CNN预测模型、EMD-ENN预测模型和SA-BP预测模型在相同数据情况下分别进行预测实验，它们的预测风速与原始风速的比较如图7（a）～（d）所示，SA-BP模型和EMD-ENN模型这两个混合预测模型的预测结果明显好于CNN模型和ARIMA模型这两个单一预测模型。为了更准确地描述这些模型预测效果的好坏，分别计算它们的评价指标MAE、MAPE和RMSE如表4所示。

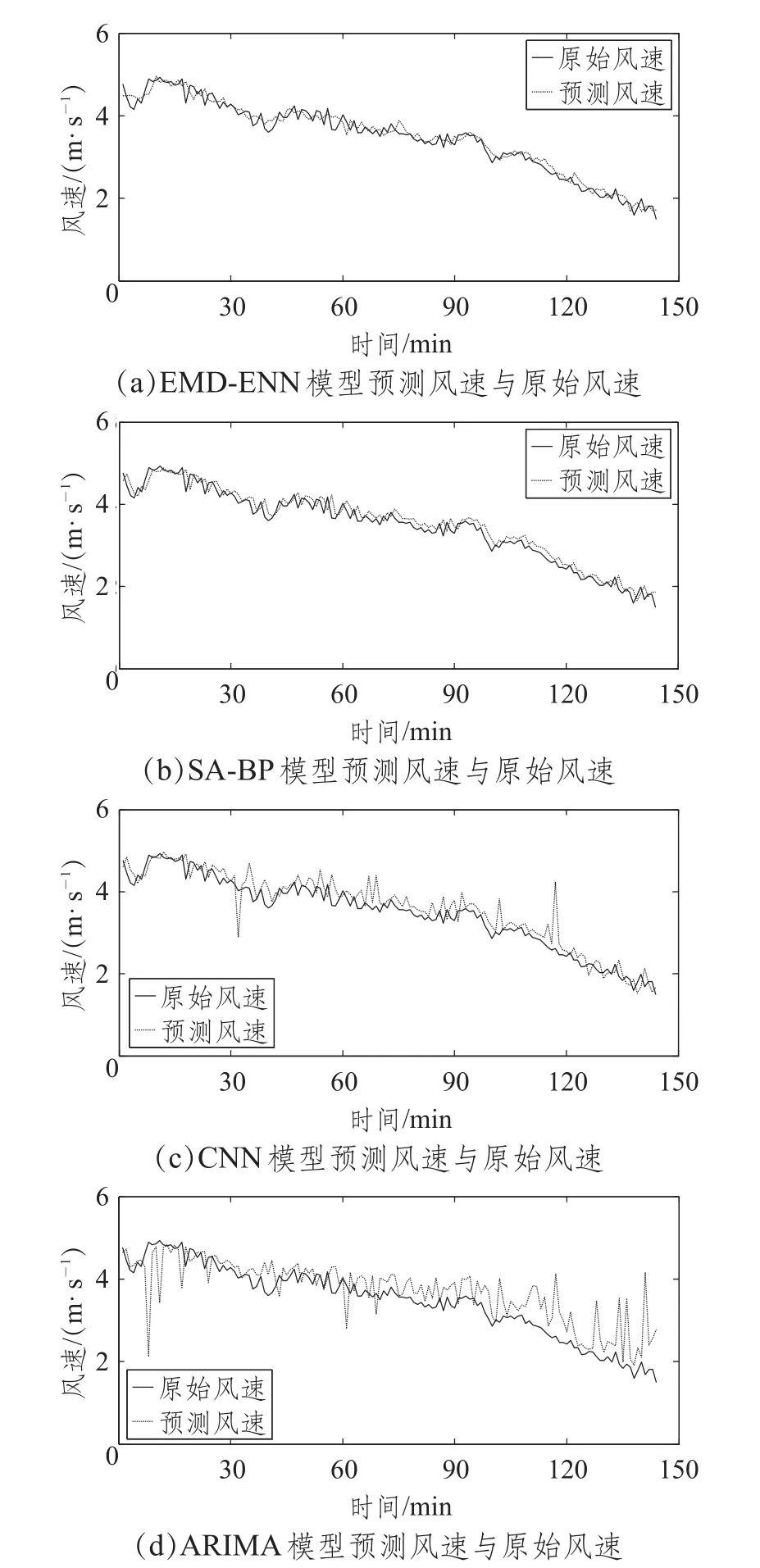
图7 其他四种模型的预测风速与原始风速的比较

表4 五种不同模型的风速预测误差

5 结束语

本文针对风速的不稳定性和多变性，提出了CEEMDWT和卷积神经网络的混合模型来提高短期风速预测的精确度。该模型的主要思路是把不稳定的风速序列转化成一些相对稳定的分量，再对每个分量进行预测重构得到最后的预测结果。通过大量实验并且与其他4个预测模型对比，该模型的预测精度更高。然而该模型中的卷积神经网络需要花费大量的时间来训练，随着卷积神经网络卷积层和子样本层层数的增加，训练时间会更大，不适用于数据量巨大的情况；而且卷积神经网络接受域的大小的确定也是一大难点，目前的方法都是凭借以往的经验。所以下一步提高预测精度的研究工作可以把该模型应用到Hadoop或Spark等大数据平台上和接受域大小的选取。

参考文献：

[1]Greene J S，Morrissey M.Estimated pollution reduction from wind farms in Oklahoma and associated economic and human health benefits[J].Journal of Renewable Energy，2013（6）：1-7.

[2]Andrés F，Daniel V.Assessing wind speed simulation methods[J].Renewable and Sustainable Energy Reviews，2015，56：473-483.

[3]Jaesung J，Robert P B.Current status and future advances for wind speed and power forecasting[J].Renewable and Sustainable Energy Reviews，2014，31：762-777.

[4]Tascikaraoglu A，Uzunoglu M.A review of combined approaches for prediction of short-term wind speed and power[J].RenewableandSustainableEnergyReviews，2014，34：243-254.

[5]Ma Lei，Luan Shiyan，Jiang Chuanwen，et al.A review on the forecasting of wind speed and generated power[J].Renewable and Sustainable Energy Reviews，2009，13（4）：915-920.

[6]Lydia M，Kumar S S，Selvakumar A I，et al.Linear and non-linear autoregressive models for short-term wind speed forecasting[J].Energy Conversion and Management，2016，112：115-124.

[7]Wang Jianzhou，Hu Jianming.A robust combination approach for short-term wind speed forecasting and analysis-combination of the ARIMA（Autoregressive Integrated Moving Average），ELM（Extreme Learning Machine），SVM（Support Vector Machine）and LSSVM（Least Square SVM）forecasts using a GPR（Gaussian Process Regression）model[J].Energy，2015，93：41-56.

[8]Liu Hui，Tian Hongqi，Li Yanfei.Four wind speed multistep forecasting models using extreme learning machines and signal decomposing algorithms[J].Energy Conversion and Management，2015，100：16-22.

[9]Wang Jujie，Zhang Wenyu，Li Yaning，et al.Forecasting wind speed using empirical mode decomposition and elman neural network[J].Applied Soft Computing，2014，23：452-459.

[10]Jiang Ping，Ge Yingjie，Wang Chen.Research application of a hybrid forecasting model based on simulated annealing algorithm：A case study of wind speed forecasting[J].Journal of Renewable and Sustainable Energy，2016，8（1）：1-17.

[11]Alex K，Ilya S，Geoffrey E H.ImageNet classification with deep convolutional neural networks[C]//Proceedings of Advances in Neural Information Processing Systems.Cambridge，MA：MIT Press，2012：1106-1114.

[12]Huang N E，Shen Zheng，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings，Mathematical，Physical and Engineering Sciences，1998，454（1971）：903-955.

[13]Wu Zhaohua，Norden E H.Ensemble empirical mode decomposition：A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1（1）：1-42.

[14]Torres M E，Colominas M A，Schlotthauer M.A，et al.A complete ensemble empirical mode decomposition with adaptive noise[C]//Proceedings of IEEE International Conference on Acoustics（ICASSP），2011：1670-1678.

[15]Alert C T，Jeffrey R M，Steven D G.Wavelet denoising techniques with applications to experimental geophysical data[J].Signal Processing，2009，89（2）：144-160.