基于突触离子通道动力学神经元网络的高效并行仿真算法*
2018-05-08王直杰顾晓春
彭 霞,王直杰,韩 芳,顾晓春
(东华大学信息科学与技术学院,上海 201620)
1 引言
生物神经网络是大量的各类神经元通过各种突触相互连接,并相互作用,实现各类神经信号的复杂传递及处理过程的复杂动力学系统。近年来,为了研究各类神经信号复杂传递过程,探索和掌握生物神经系统的各种功能机理,全球计算神经科学专家建立了大量的生物神经网络数学模型,并通过计算机软、硬件技术,研发了大量系统仿真软件平台,如GENESIS(the GEneral NEural SImulation System)[1]、NEURON[2,3]、NEST[4]、蓝色大脑项目[5]等对神经网络系统进行模拟仿真[6,7]。
生物神经元和突触的动力学特性非常复杂,生物神经网络系统仿真模拟的计算量非常大,譬如,对一个神经元个数N=104的全连接采用递质-受体(Neurotransmitter-receptor)离子通道动力学[8,9]的复杂突触模型的生物神经网络,每一突触后末梢有103个受体,若采用传统时钟同步算法[6,10,11]进行该生物系网络系统的模拟仿真,在每一时间步内,包含N(104)次神经元膜电位计算和约N2(108)次突触电流计算,并且每一突触电流涉及的受体浓度计算包括受体个数(103)次绑定和解绑转化过程的计算。这意味着,每一时间步的每一条突触的输入电流计算涉及到大量的复杂离子通道动力学模型的计算,整个系统模拟的计算量尤其是突触计算量是相当惊人的,单处理器架构下大规模生物神经网络模拟仿真将变得非常困难。因此,当神经网络的神经元及突触规模达到一定数量时,生物神经网络的仿真需要大规模并行计算技术。因图形处理器GPU(Graphics Processing Units)[12,13]是强大的计算平台,且相对于采用大规模并行计算机而言,它具有价格低、使用方便等特点,本文采用GPU硬件平台和英伟达NVIDIA公司的统一计算设备架构CUDA(Compute Unified Device Architecture)开发工具进行生物神经网络并行算法的设计。
为了提高大规模神经元网络系统在GPU上的并行仿真效率,通过分析整个网络的计算过程发现,仿真计算量主要包括每个神经元膜电位的计算和更新以及每条突触电流的计算和更新两部分;某时刻,某条突触电流的计算不但与该突触后神经元当前时刻的状态相关,与突触的神经递质传递信号时延以及具体突触特性相关,还跟突触前神经元的所有历史放电状态有关。可以看出,突触电流计算中,突触前神经元和突触后神经元的状态共同决定突触的状态,突触前后神经元的耦合度非常高。因此,降低突触电流计算时突触前后神经元之间的耦合度是设计计算模块独立性强、模块间耦合度低的高效生物神经网络并行算法的关键。
本文通过分析化学突触信息传递机理及递质-受体离子通道动力学特征,提出了突触前神经元释放的递质浓度计算与突触后神经元已绑定受体浓度计算分离的思想,即递质-受体计算分离思想,大大增强了这两个计算过程的独立性,有效降低突触电流计算中突触前神经元和突触后神经元的耦合度,并基于此思想设计一种计算模块独立性强、模块间耦合度低的并行算法,提高了生物神经网络并行仿真效率。
2 具有复杂突触动力学的生物神经网络模型
本文以全连接网络结构、IAF (Integrate-And-Fire)神经元模型[14,15]及递质-受体离子通道动力学突触模型的生物神经网络模型为例设计并行仿真算法(其它类型的网络模型的仿真算法可类似设计,如神经元为H-H(Hodgkin-Huxley)方程[16]描述的模型)。
2.1 神经元计算模型
基于IAF神经元模型的全连接神经网络可用动态方程(1)表示。
(1)
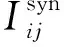
通过Euler数值计算方法对公式(1)进行差分计算,设步长为h=Δt,则神经元在时间步t+1的膜电位Vi(t+1)可由公式(2)来计算。
Vi(t+1)=Vi(t)+
(2)
2.2 递质-受体离子通道动力学突触计算模型
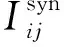
(3)
其中,th为时间常数,h(t)在t=th时取峰值h(th)=e-1/th,qmax为递质分子浓度最大值,t0为突触前神经元的放电时刻,时间常数tq决定了q(t)的衰减快慢。
根据化学突触的动力学机理[8],突触传递递质分子T绑定突触后末梢的各类受体R(Receptor)的动力学过程可用动力学过程(4)表示。
(4)
其中,R表示突触后末梢上未与递质分子绑定的受体;TR*表示突触后末梢已经与递质分子绑定的受体;α是受体从未绑定到与递质分子绑定的状态转化率常数;β是受体从绑定状态转化到未绑定状态的转化率常数,转化率常数由具体突触本身特性决定,其值越大,表明在同一时间段内受体状态转换越快。公式(4)表示在每一单位时间Δt,任何一个绑定的受体,有β的可能转化为未绑定,对于任意未被绑定的受体有αq(t)的可能转化成已绑定状态。
神经元j到神经元i之间的突触记为:j→i,t时刻,突触电导记为Gij(t),设突触后神经元的末梢的受体总数为NR,分别分布在突触后末梢的第k(k=1,…,NR)个位置,受体跟突触间隙的递质分子结合并绑定,从而使得突触后末梢该受体位置的离子通道门打开,gk(t)为k位置的单离子通道门开度,突触单离子通道门的最大开度即最大电导为gc,已绑定递质的受体个数(记为nc(t))直接决定实际整个突触j→i此时刻的离子通道门的开度。因此,对于每条突触,在任意t时刻,突触电导Gij(t)可以用以下公式表示:
(5)
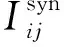
(6)
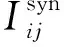
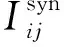

gc·nc(t)·(Esyn-Vi)
(7)
下面本文将根据突触信息传递机理及突触动力学特性来分析突触电流计算特点,为降低突触电流计算中突触前后神经元的耦合度,提出递质-受体计算分离的思想,从而设计一种基于突触离子通道动力学特征的神经元网络并行算法,实现生物神经网络的高效并行仿真。
3 递质-受体计算分离思想
本文采用时钟同步算法进行生物神经网络系统的模拟,传统意义上的时钟同步算法框架如图1所示,在每一时钟步Δt,针对每一个神经元进行神经元状态的计算,包括两部分:对神经元连接的每条突触进行输入突触电流计算(公式(3)、公式(4)和公式(7)),并累加获得该神经元总的突触输入电流;计算每一神经元的膜电位(公式(2))。时钟不断向前推进,实现整个网络的仿真。
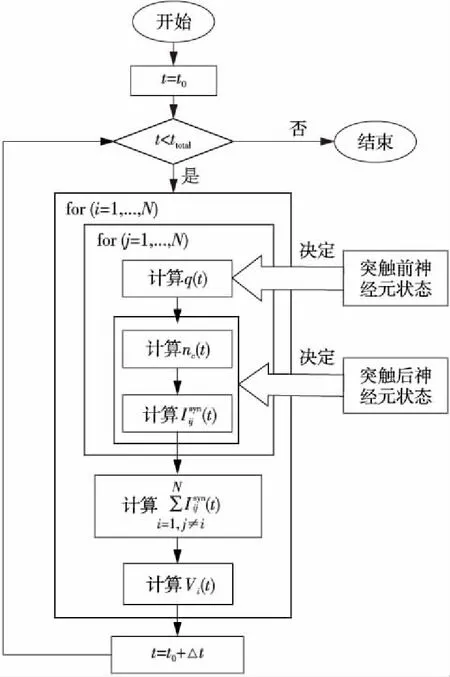
Figure 1 Flow of neuronal network serial simulation图1 神经元网络串行仿真流程图
结合公式(2)~公式(4)和公式(7),对于由N个神经元组成的全连接网络,在每一时间步,主要包括四个主要计算部分:N(N-1)次突触前神经元产生的递质分子浓度q(t)计算;对每条突触要通过NR个随机过程来统计已绑定的该突触后末梢受体个数,并且由文献[8]可知,NR越大,离子通道动力学突触模型中突触电导Gij(t)函数曲线将越平滑,因此共有NR·N(N-1)次突触后受体nc(t)计算;N(N-1)次突触电流计算;N次神经元的膜电位Vi(t)计算。可以看出,当神经网络规模增大、模型的复杂度增加时,整个网络的计算量急剧增大,而且绝大多数的计算都耗费在突触电流的计算上。因此,大规模神经元网络的模拟仿真需要并行计算,而且并行算法设计中,突触电流计算的并行策略设计尤其重要。
然而,从图1可以看出,从神经元j到神经元i的突触电流计算包括三部分:与突触前神经元放电状态相关的递质分子浓度计算;突触后神经元末梢已绑定受体的统计计算;突触后神经元的输入电流计算。每条突触电流计算过程中,突触后神经元上已绑定受体个数的统计计算必须要获得当前时刻的递质分子浓度q(t),而此时刻递质分子浓度跟突触前神经元历史放电信息以及突触信息传递时延等有关,这意味着,每条突触电流计算过程中,突触前神经元和突触后神经元状态信息之间耦合度很高。如何减少突触电流计算中突触前后神经元之间的耦合度,是设计高效神经元网络并行算法的关键问题。
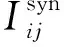
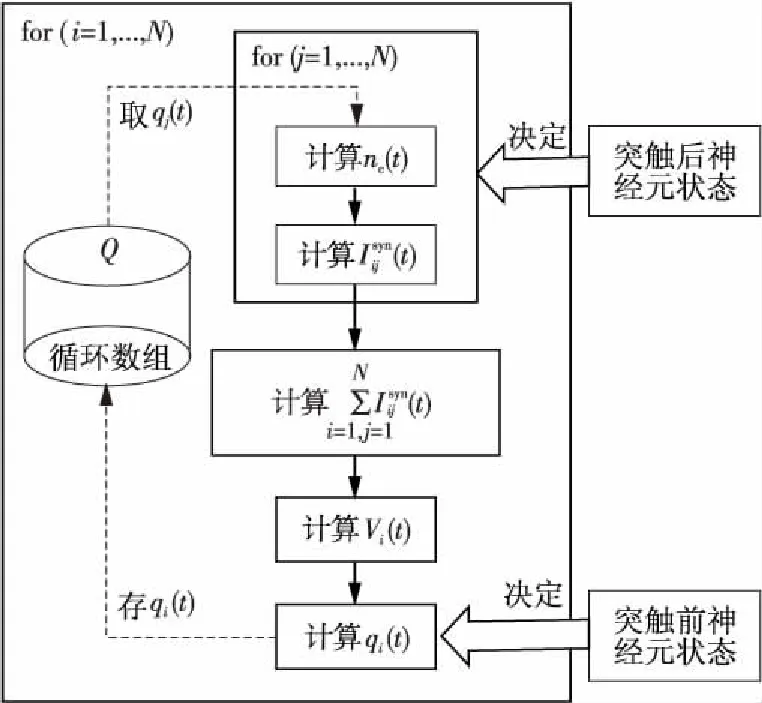
Figure 2 Core framework of the algorithm based on neurotransmitter-receptor computing separation图2 基于递质-受体计算分离的核心算法框架
从基于递质-受体计算分离思想的神经元网络核心算法可以看出,通过直接从循环数组Q中获取突触前神经元的信息,突触电流计算主要由突触后神经元的状态决定;而由突触前神经元状态决定的递质分子浓度q(t),从突触电流计算中分离出来,通过直接获取突触前神经元膜电位等信息直接计算并保存到数组Q中;显然,每条突触电流计算时,突触前神经元和突触后神经元状态之间的耦合度通过引入循环数组Q而得到显著降低。因此,整个网络计算量最大、耦合度最高的突触电流计算模块的独立性得到了很大的提高,有利于提高大规模生物神经网络并行仿真效率。
4 基于递质-受体计算分离的神经元网络并行算法
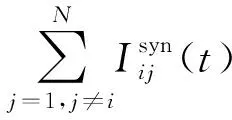
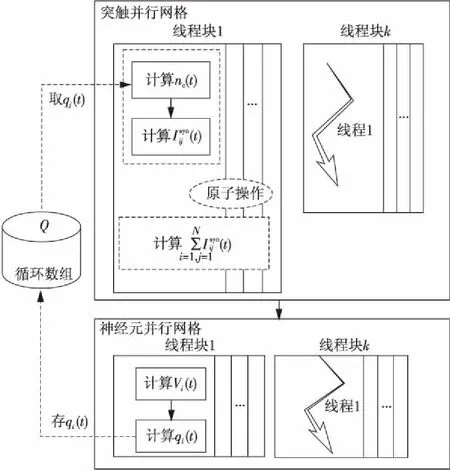
Figure 3 Parallel strategy of the algorithm based on neurotransmitter-receptor computing separation图3 基于递质-受体计算分离算法的并行策略
根据图3所示策略,本文设计了基于递质-受体计算分离的神经元网络仿真并行算法如下:
t=t0;
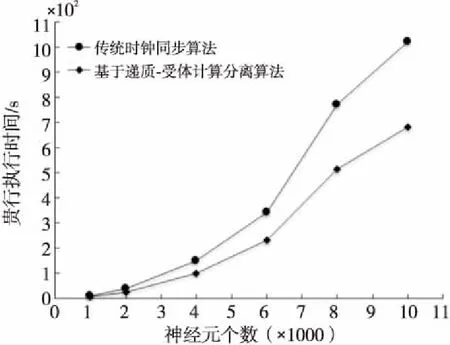
whilet /*GPU上执行,每条线程对应一条突触电流计算,并行实现每个神经元的总输入电流计算*/ (1)计算突触后末梢的被绑定受体数nc1: nc-new=0;//新绑定的受体个数 nc-left=nc0;//当前时刻已绑定的受体个数 从j的长度为Dmaxdelay的循环数组Q的(j,(t-dij)modDmaxdelay)位置获取突触前神经元j产生的递质分子浓度q(t); For每个未绑定的受体R(共NR-nc0个):产生随机数,若大于α·q(t),则该未绑定的受体转变成已绑定,即:nc-new=nc-new+1; For每个已绑定的受体TR*(共nc0个):产生随机数,若大于受体的解绑率常数β,则该绑定受体将解绑成未绑定状态,即nc-left=nc0-1;nc1=nc-new+nc-left; /*GPU上执行,每一条线程对应每个神经元的膜电位及递质浓度计算*/ 步骤3根据公式(2)计算神经元i在t时刻的膜电位Vi(t); 步骤4计算突触前神经元状态及其产生的递质浓度: if(Vi(t)>Vth),重置神经元i的膜电位:Vi(t)=0;根据公式(3)计算神经元i的虚拟突触在t时刻的递质浓度q(t-t0)并存储到循环数组Q的(i,tmodDmaxdelay)位置; else 根据公式(3)计算神经元i的虚拟突触在t时刻的递质浓度q(t)并存储到循环数组Q的(i,tmodDmaxdelay)位置; end if //CPU上执行,时钟推进 t=t0+Δt; end while 本文在单机上分别针对基于递质-受体计算分离的神经元网络时钟同步串行算法、传统时钟同步算法进行了神经元网络系统模拟仿真实验,并在单NVIDIA GPU模式下使用CUDA对基于递质-受体计算分离的神经元网络并行算法进行并行模拟实验,实验测试软件平台为NVIDIA GeForce GTX 960,4 GB显存,Windows 8.0,Visual Studio 2015,C++语言,机器主机频率4.2 GHz,内存8 GB。生物神经网络采用包含兴奋性、抑制性两类IAF神经元及递质-受体离子通道动力学突触模型(受体个数NR=1000)的全连接网络。模拟50 ms(5 000步)生物时间,步长为0.01 ms,网络中最大延迟步长为2 ms(200步)。 对基于递质-受体计算分离的时钟同步串行算法及传统时钟同步串行算法分别进行了上述神经元网络系统的模拟仿真实验,其结果如图4所示,当网络的神经元数量大于3 000时,新算法的串行执行时间与传统时钟同步算法相比,明显减少,并且随着网络规模的增大,减少的幅度更加明显。这是因为,对于每一时间步,传统时钟同步算法中每条突触电流的计算包含递质浓度的计算和受体浓度的计算,递质浓度q(t)的计算次数为突触数量次,即N·(N-1),而将递质浓度计算从突触电流计算中分离出来,只要在进行每个突触前神经元的膜电位计算时进行该神经元引起的递质浓度计算,因此每一时间步递质浓度计算次数减少到神经元数量次,即N。当神经元数量较少时,突触数量相对不大,突触电流计算中的递质浓度计算量虽然得到减少,但对整个算法的性能改善不明显;而当网络规模扩大时,基于递质-受体计算分离算法的串行执行效率较传统时钟同步算法串行执行效率优势逐渐明显。因此可以看出,随着网络规模的扩大,基于递质-受体计算分离的新时钟同步算法提高了传统时钟同步算法的性能。 Figure 4 Serial simulation results of traditional algorithm and the new algorithm with different neural network scales图4 不同网络规模下的传统时钟同步算法 与新算法的串行仿真结果 采用基于递质-受体计算分离的并行算法在不同规模下对上述神经元网络模拟实验的加速比及GPU运行时间如图5a和图5b所示(注:分别采用尺寸为640、1 024的一维线程块)。从图5a可以看出,本文提出的并行算法对神经元网络并行仿真时,其加速比整体上随着网络规模的增大而快速增加。这是因为随着整个网络规模N的扩大,突触数量N·(N-1)迅速增大,每一时间步的突触电流计算次数N·(N-1)也将迅速增长,并且每一时间步内突触电流计算中,突触受体浓度计算量(每一时间步有NR·N·(N-1)次)急剧增大,使得基于递质-受体计算分离的串行算法的执行时间急剧增大。而基于递质-受体计算分离的时钟同步并行算法的映射策略是采用每条突触电流计算(包括突触受体浓度计算)对应每条GPU线程,这些线程大量并行执行。因此,相对于串行算法执行时间增加幅度而言,并行算法在GPU上执行时间的增加比较平缓(图5b),所以并行算法的加速比增长速度较快(图5a)。然而当网络规模达到6 000或10 000附近(块尺寸分别为640和1024)的两条加速比曲线都出现了小幅度的下降(图5a)。这是GPU硬件结构特点导致的,因为随着网络规模的扩大,神经元数量以及突触数量每达到硬件一次上下文切换的线程条数时,都将要进行上下文切换,这一特点影响了突触电流并行和神经元状态计算并行两模块的执行时间,从而表现出整个算法在某些网络规模(6 000、10 000)下出现GPU并行执行时间加速上升(图5b),导致图5a中两条加速比曲线在相应的规模下出现小幅度的下降,但随后两条加速比曲线又随着网络规模的增大而增加。因此,本文提出的并行算法随着网络规模的增大整体上表现出很好的并行性能。 Figure 5 Performance of the parallel algorithm图5 并行算法的性能 上述仿真实验结果表明,与传统时钟同步算法相比,本文提出的递质-受体计算分离算法既减少了传统时钟同步算法中递质浓度计算量,提高了传统时钟同步算法的性能,还通过将递质浓度计算从突触电流计算中分离出来单独计算,降低了突触电流计算中突触前神经元和突触后神经元之间状态耦合度,更有利于占整个网络最大计算量的突触电流计算部分的并行化实现。因此,本文提出的基于递质-受体计算分离的并行算法对大规模的含复杂突触模型的神经元网络的模拟仿真是高效的。 本文通过分析化学突触递质分子和受体离子通道动力学特征,提出了递质-受体计算分离的思想,增强了突触前神经元引起的递质分子浓度计算与突触后绑定状态的受体计算之间的独立性,降低突触电流计算中突触前神经元状态和突触后神经元状态之间的耦合度。基于递质-受体计算分离的思想,通过不同的映射策略分别实现了突触前神经元的状态信息并行计算和突触电流的并行计算,从而设计了一种大规模生物神经网络并行算法。仿真结果表明了该算法的高效性。 参考文献: [1] Basu I,Kudela P,Korzeniewska A,et al.A study of the dynamics of seizure propagation across micro domains in the vicinity of the seizure onset zone[J].Journal of Neural Engineering,2015,12(4):046016. [2] Carnevale N T,Hines M L.The NEURON book[M].Cambridge:Cambridge University Press,2006. [3] Kim D,Paré D,Nair S S.Mechanisms contributing to the induction and storage of Pavlovian fear memories in the lateral amygdala[J].Learning & Memory,2013,20(8):421-430. [4] Jan M,Tomohiro S,Kenji D.The mechanism of saccade motor pattern generation investigated by a large-scale spiking neuron model of the superior colliculus[J].Plos One,2013,8(2):e57134. [5] Markram H.The blue brain project[J].Nature Rev Neurosci,2006,7(2):153-160. [6] Brette R,Rudolph M,Carnevale T,et al.Simulation of networks of spiking neurons:A review of tools and strategies[J].Journal of Computational Neuroscience,2007,23(3):349-398. [7] Milkowski M. Explanatory completeness and idealization in large brain simulations:A mechanistic perspective[J].Synthese,2016,193(5):1457-1478. [8] Chapeau-bloudeau F, Chambet N.Synapse models for neural networks:From ion channel kinetics to multiplicative coefficient wij[J].Nueral Computation,1995,7(4):713-734. [9] Destexhe A,Mainen Z F,Sejnowski T J.Synthesis of models for excitable membranes,synaptic transmission and neuromodulation using a common kinetic formalism[J].Journal of Computational Neuroscience,1994,1(3):195-230. [10] Hanuschkin A,Kunkel S,Helias M,et al.A general and efficient method for incorporating precise spike times in globally time-driven simulations[J].Frontiers in Neuroinformatics,2010,4(8):113. [11] Lin Xiang-hong.Simulation and evolution of large-scale spiking neural networks[D].Harbin:Harbin Institute of Technology,2009.(in Chinese) [12] Nageswaran J M,Dutt N,Krichmar J L,et al.2009 special issue:A configurable simulation environment for the efficient simulation of large-scale spiking neural networks on graphics processors[J].Neural Networks the Official Journal of the International Neural Network Society,2009,22(5-6):791-800. [13] Brette R,Goodman D F.Vectorized algorithms for spiking neural network simulation[J].Neural Computation,2011,23(6):1503-1535. [14] Dayan P,Abbott L F.Theoretical neuroscience[M]. Massachusetts:MIT Press,2001:154-155. [15] Brette R.Exact simulation of integrate-and-fire models with synaptic conductances[J].Neural Computation,2006,18(8):2004-2027. [16] Hodgkin A L,Huxley A F.Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo[J].Journal of Physiology,1952,116(4):449. [17] Li Lian-jiang.Research on GPU based spiking neural network learning [D].Wuhan:Huazhong University of Science and Technology,2015.(in Chinese) 附中文参考文献: [11] 蔺想红.大规模脉冲神经网络的模拟与进化研究[D].哈尔滨:哈尔滨工业大学,2009. [17] 李连江.基于GPU的脉冲神经网络学习研究[D].武汉:华中科技大学,2015.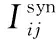
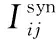
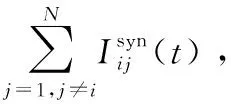
5 仿真结果及性能分析

6 结束语
