采用符号动力学方法检测低速率拒绝服务攻击
2018-05-08杨宝旺
杨宝旺
(宁波大学 科学技术学院,浙江 宁波 315212)
采用符号动力学方法检测低速率拒绝服务攻击
杨宝旺
(宁波大学 科学技术学院,浙江 宁波 315212)
针对低速率拒绝服务攻击引起的网络安全问题,提出采用符号动力学方法对其进行检测,通过将采样得到的数据包数量信号转化为对应的符号序列,并计算符号序列的熵值,发现低速率拒绝服务攻击具有令数据包数量信号信息复杂度激增的特点,从而能够结合预先设定的熵阈值进行比较识别.分别在仿真环境和实际测试服务器上进行了算法验证,实验结果表明,文中所提算法对低速率拒绝服务攻击辨识平均准确度超过92%.
低速拒绝服务攻击;符号动力学;熵;信息复杂度;阈值;网络安全
拒绝服务(Denial-Of-Service, DOS)攻击是互联网常见的恶意攻击,其通过高频高速率地产生大量无用数据占据被攻击目标的访问带宽,从而使其他正常用户与被攻击对象的数据交换变得缓慢甚至瘫痪[1-3].随着互联网信息安全技术的发展,传统DOS攻击因为统计特性显著区别于正常数据流,通过流量监控和数据包扫描,可以有效地甄别出这种攻击模式.然而,近年来却出现了传统DOS攻击的多种变体,主要分为分布式拒绝服务(Distributed-Denial-Of-Service,DDOS)攻击以及低速率拒绝服务(Low-rate-Denial-Of-Service,LDOS)攻击[4-5],其中LDOS因为利用了网络协议或应用服务器的自适应机制中的安全漏洞,攻击形式更加隐蔽,在攻击方式和原理上都明显区别于DOS以及DDOS,成为互联网信息安全领域的研究热点[6-7].
LDOS攻击最明显的特点是只在特定周期性的短暂时间区间内发送大量攻击数据,而在其他时间内并不进行其他攻击性行为.这种周期性攻击的特点使得LDOS攻击整体平均数据速率很低,难以被监测,却能使得受害者端的数据交互效率显著降低.过往对于LDOS攻击的检测一般也主要从识别其周期参数入手,基于时域统计建模[8-11],结合统计参数分析,以及进一步引入动态随机过程模型检测数据分布变化特征,或者基于信号变换技术[12-15],分析其功率谱、小波域不同尺度的分量特性等.
这些算法对于LDOS攻击检测的焦点主要是放在了攻击带来的周期性信号能量的改变,却忽视了周期性攻击所带来的数据信号信息量的差异,其数据在一段时间内的整体熵值将会相应改变.经典的时间序列熵值计算方法包括香农熵、近似熵、样本熵和符号动力学熵等,网络数据流所构成的随时间变化的信号,数据流量出现阶梯式变化特点,并不适于采用近似熵或者样本熵进行分析[16-17].笔者提出采用符号动力学熵方法进行LDOS攻击检测,通过分析采集得到的攻击以及非攻击数据流的序列信息复杂度,能够实现对于LDOS攻击的准确识别以及持续时间判断,从而有效阻拦并辅助剔除此类信息安全攻击,保障服务器正常运行.
1 符号动力学以及符号动力学熵
网络数据流是存在于不同终端之间的随时间变化的信号,LDOS攻击可以建模为一种由攻击服务器和受到影响的网络空间的数据流量时间序列叠加生成的非平稳信号.符号动力学正是将这种数据信号序列抽象和粗粒化后,分析其不同行为模式的方法.这里对于数据序列的粗粒化能够消除噪声对于序列信息量的影响,反应出时间序列的信息复杂度.
网络数据流时间序列简单的粗粒化符号描述,可以通过对原始采样数据集进行阈值对比和分割来实现.
采集一段网络数据流时间序列X{xi|i=1,2,…,N},上述序列X系统性能可以由一个M个符号组成的符号集{s0,s1,…,sM-1)和一个M+1 个临界点组成的集合{c0,c1,…,cM}进行描述,进而可以将网络数据流X转换为一个与其对等的符号序列X{s(j)|j= 1,2,…,N},具体转化规则如下:
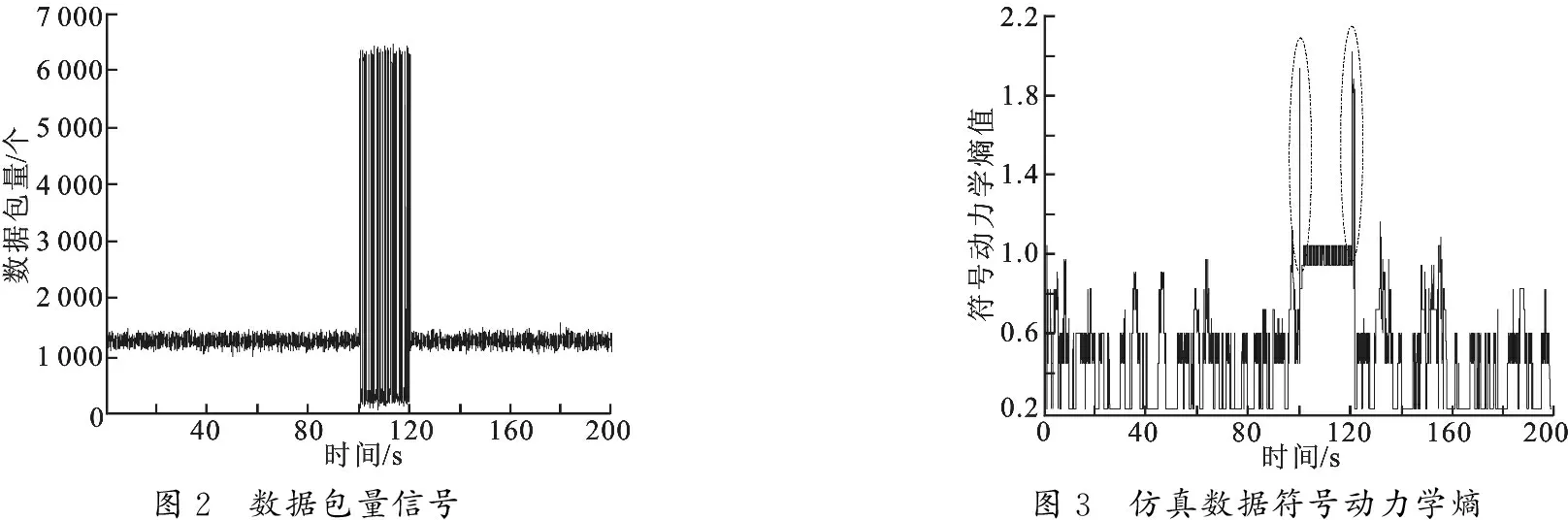
(1) 符号化.如果ck (2) 给定一个长度为L的窗体,将X{s(j)|j=1,2,…,N}符号序列分割成长度为对应的片段序列u(i)= [s(i),s(i+1), …,s(i+L- 1)]. (3) 将每一个片段序列构成的符号码组成为矩阵u(1),…,u(N-L+1),这些片段序列可以简化统一标记如下: 其中,m对应序列{si|i=0,1,2,…,M-1}中不同整数的数量,i代表符号化后的片段序列的起始位置. (4) 用整数K替代对应的符号sK,代入lx(L,i),可以得到每个片段序列对应的整数数值V,这里V属于整数集{0,1,…,ML-1},且每个lx(L,i)存在和仅存在惟一的一个整数与其对应.网络数据流X符号化转化完毕. 对于整数转化后的符号序列,可以进一步定义其符号动力学熵,具体定义为 其中,Plx=nlx/nsum,是lx出现的频率,nlx是lx出现的次数,而nsum是符号化后的片段序列的总数.文中对于网络流信息序列的辨识具体采用一个三符号{s0,s1,s2}系统,其分别对应整数{0,1,2},用于将原始采样序列划分为不用符号的阈值为采样信号均值的上下 1±α倍,这里α∈ (0.1, 0.5),L=3,则原始采样数据流信号可以依次每3个数值惟一转化为 1~ 27中的一个整数. 图1 NS2仿真网络拓扑 为了验证基于符号动力学熵方法对于LDOS攻击的检测能力,文中同时在基于NS2仿真模拟平台和实际测试网络服务器上进行.其NS2仿真模拟平台对应的网络拓扑结构如图1所示,LDOS攻击算法采用基于Linux传输控制协议(Transmission Control Protocol,TCP)核生成的Shrew攻击序列[14],通过用户数据报协议(User Datagram Protocol,UDP)软件生成攻击流.网络流数据包被采样,计算符号动力学熵值反映时序信号的信息复杂度. 基于NS2仿真实验环境的网络拓扑结构采用非对称哑铃形态,其包含两个路由器R0和R1,4组合法的TCP数据发送端N1~N4和接受端S1~S4,以及1个UDP-LDOS攻击端A1.除了两个路由器之间加入随机早起检测(Random Early Detection,RED),限制了接受和发送之间的数据流速率为 10 Mbit/s 以外,其他连接之间的网络数据流速率均为 100 Mbit/s.网络最小恢复时间目标(Recovery Time Objective,RTO)为 1 000 ms,模拟周期为 200 s,攻击起始为第 100 s,持续时间为 20 s,对应的LDOS攻击参数LDOS(T,Len,R)为 (1 100 ms,200 ms,10 Mbit/s). 对于符号动力学熵值计算,可以基于一个滑动的时间窗口W,为了兼顾计算的时效性,一般W内的采样点数的数量为 100~ 1 000,以生成能够反应检测时间区间内稳定的符号化分布.图2展示了利用NS2平台模拟生成的带有仿真LDOS攻击的时间序列.可以看出,在引入了LDOS攻击之后,数据包数量出现了明显增加. 图2 数据包量信号图3 仿真数据符号动力学熵 图2中仿真信号的符号动力学熵,在图3中给出了对应的熵值时间序列.在攻击开始和结束时,符号动力学熵出现了明显增加,如图3虚线椭圆框中所示,其熵值接近是普通正常数据传输的两倍,体现对攻击序列检测的敏感性.同时,在攻击持续过程中,其熵值也大于多数正常时间的熵值,攻击过程中熵值的降低是因为此时有多个攻击序列存在于检测窗口内.这些相似的攻击信息,被符号动力学熵识别为同一类型数据模式,从而使得其整体信息复杂度降低. 进一步,设置一个熵门限阈值δ,采用简单的阈值比较进行攻击时间的检测和筛选.将上述实验重复100次,每次随机添加攻击的起始时间和持续时间,从中随机选取50组,采用一个线性分类器[18]学习门限阈值δ,再用剩余的50组进行检测验证,测试一共进行了4次,后3次在检测的数据流中引入一个随机白噪声,白噪声的均值为零,标准差分别为数据包量平均量的10%、20%和30%,得到相应的检测准确度如表1所示. 在不同的外加噪声影响下,基于符号动力学检测方法的稳定性一直保持良好,噪声对于检测精度的影响主要体现在使得整体检测的精确度的波动范围更大.为了更好地说明中文方法的实际应用效果,将上述符号动力学熵检测方法在实际测试网络服务器上进行了验证.测试服务器组的网络拓扑结构如图4所示. 实验环境的网络拓扑结构包含:1个思科路由器,4个正常用户TCP数据发送端用户1~用户4,一个 100 M 网关以及文件传输协议(File Transfer Protocol,FTP)服务器.黑客攻击端,网络连接之间的网络数据流速率均为 100 Mbit/s.LDOS攻击参数LDOS(T,Len,R)为 (1 100 ms,200 ms,10 Mbit/s).随机进行攻击行为100次,每次攻击的时间起点随机,持续时间取值服从 20~ 60 s 的均匀分布,每段采样信号检测时间长度为 200 s,同样利用线性分类器训练50组样本得到一个对应的符号动力熵阈值,如图5所示. 最后,文中提出的算法与现有技术中的基于时域滤波方法,例如卡尔曼滤波检测方法[9]、频域变换方法和NCAS方法[7],进行了计算结果准确性以及算法复杂度的对比,对于实际采集的数据,在四核型号为Intel(R)Core(TM)i5-4460 CPU @3.20 GHz 的处理器运行上述3种算法对比,具体对比结果如表2所示. 表2 不同算法的检测结果比较 可见,基于符号动力学熵的计算方法在计算时间复杂度以及准确性上,都优于常见的基于频域或者时域的检测算法,检测精确度提高了2%以上,且算法的计算复杂度低,更加便于实施和工程应用. 文中提出的将符号动力学方法应用于LDOS攻击检测,并通过检测符号动力学熵的方法进行攻击行为甄别.符号动力学将原始采集的数据包信号转化为更容易表征其序列信息模式的符号序列,在通过熵值计算反应出LDOS攻击所带来的信息量激增特征,将LDOS检测转变为识别时间序列信息复杂度检测问题,并结合简单的阈值比较,实现了对LDOS攻击的准确、高效识别. 参考文献: [1] WOOD A D, STANKOVIC J A. Denial of Service in Sensor Networks[J]. Computer, 2002, 35(10): 54-62. [2] ZHANG H, CHENG P, SHI L, et al. Optimal Denial-of-service Attack Scheduling with Energy Constraint[J]. IEEE Transactions on Automatic Control, 2015, 60(11): 3023-3028. [3] MAHIMKAR A, DANGE J, SHMATIKOV V, et al. Dfence: Transparent Network-based Denial of Service Mitigation[C]//Proceedings of the 4th USENIX Conference on Networked Systems Design & Implementation. Berkeley: USENIX Association, 2007: 24. [4] 梁洪泉, 吴巍. 利用节点可信度的安全链路状态路由协议[J]. 西安电子科技大学学报, 2016, 43(5): 121-127. LIANG Hongquanl, WU Wei. Secure Link Status Routing Protocol Based on Node Trustworthiness[J]. Journal of Xidian University, 2016, 43(5): 121-127. [5] YAN Q, YU F R, GONG Q, et al. Software-defined Networking (SDN) and Distributed Denial of Service (DDoS) Attacks in Cloud Computing Environments: a Survey, Some Research Issues, and Challenges[J]. IEEE Communications Surveys and Tutorials, 2016, 18(1): 602-622. [6] ZHANG C W, YIN J P, CAI Z P, et al. RRED: Robust RED Algorithm to Counter Low-rate Denial-of-service Attacks[J]. IEEE Communications Letters, 2010, 14(5): 489-491. [7] BAI Y, XIE C Y, QIN J C. Research of Three-level Detection Algorithm Against Low-rate Denial of Service Attacks[J]. Advanced Materials Research, 2012, 403/404/405/406/407/408: 2325-2328. [8] ARAVIND B, NARAYANA M L. Detecting Constant Low-frequency Appilication Layer DDOS Attacks Using, Collaborative Algorithms[J]. International Journal of Computer Trends & Technology, 2013, 4(10): 1132-1139. [9] YU C, KAI H, YU-KWONG K. Collaborative Defense Against Periodic Shrew DDoS Attacks in Frequency Domain[J]. ACM Transactions on Information and System Security, 2005(3): 59-67. [10] 吴志军, 岳猛. 基于卡尔曼滤波的LDDoS攻击检测方法[J]. 电子学报, 2008, 36(8): 1590-1594. WU Zhijun, YUE Meng. Detection of LDDoS Attack Based on Kalman Filtering[J]. Acta Electronica Sinica, 2008, 36(8): 1590-1594. [11] ZHANG X Y, WU Z J, CHEN J S, et al. An Adaptive KPCA Approach for Detecting LDoS Attack[J]. International Journal of Communication Systems, 2017, 30(4): e2993. [12] WU Z J, JIANG J, YUE M. A Particle Filter-based Approach for Effectively Detecting Low-rate Denial of Service Attacks[C]//Proceedings of the 2016 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery. Piscataway: IEEE, 2017: 86-90. [13] KANG J, YANG M, ZHANG J Y. Accurately Identifying New QoS Violation Driven by High-distributed Low-rate Denial of Service Attacks Based on Multiple Observed Features[J]. Journal of Sensors, 2015, 2015(2015): 465402. [14] WU Z J, ZHANG L Y, YUE M. Low-rate DoS Attacks Detection Based on Network Multifractal[J]. IEEE Transactions on Dependable and Secure Computing, 2016, 13(5): 559-567. [15] AIN A, BHUYAN M H, BHATTACHARYYA D K, et al. Rank Correlation for Low-rate DDoS Attack Detection: an Empirical Evaluation[J]. International Journal of Network Security, 2016, 18(3): 474-480. [17] CORDOVA J, NAVARRO G. Practical Dynamic Entropy-compressed Bitvectors with Applications[C]//Lecture Notes in Computer Science: 9685. Heidelberg: Springer Verlag, 2016: 105-117. [18] 李青茹. 网络蠕虫的传播模型及其检测技术研究[D]. 西安: 西安电子科技大学, 2016. Low-rate-denial-of-serviceattackdetectionbysymbolicdynamicsmethod YANGBaowang (College of Science & Technology, Ningbo Univ., Ningbo 315212, China) In terms of the network security problem caused by Low-rate-Denial-of-Service attack, this paper proposes a symbolic dynamics method to detect such attacks. The number of packets sampled signals is transferred into the symbol sequence and the calculate the entropy corresponding to the symbol sequence. There is a significant increase in packets number signal information complexity caused by Low-rate-Denial-of-Service attack arrival, which can be compared with a default entropy threshold for recognition. We verify the algorithm in the simulation environment and the actual test servers respectively and the experimental results show that the proposed algorithm has an average accuracy of 92% to achieve the Low-rate-Denial-of-Service attack recognition. low-rate-denial-of-service attack;symbolic dynamics;entropy;information complexity;threshold;network security 2017-05-15 时间:2017-07-04 国家自然科学基金资助项目(61573235) 杨宝旺(1983-),男,硕士,E-mail: yangbaowang@nbu.edu.cn. http://kns.cnki.net/kcms/detail/61.1076.TN.20170704.1644.002.html 10.3969/j.issn.1001-2400.2018.01.025 TN911.7 A 1001-2400(2018)01-0140-05 (编辑: 齐淑娟)
2 实验平台搭建与结果验证

3 结 束 语
