方位多通道HRWS SAR多普勒中心稳健估计算法

房 超， 刘艳阳， 李真芳， 任 伟， 陈筠力

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071； 2. 上海卫星工程研究所 雷达总体与仿真技术实验室，上海 201109; 3. 上海航天技术研究院，上海 201109)

方位多通道HRWS SAR多普勒中心稳健估计算法

房 超1， 刘艳阳2， 李真芳1， 任 伟2， 陈筠力3

(1. 西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071； 2. 上海卫星工程研究所 雷达总体与仿真技术实验室，上海 201109; 3. 上海航天技术研究院，上海 201109)

在方位多通道高分辨宽测绘带合成孔径雷达系统中，为了解决回波多普勒中心估计问题，提出了一种新的多普勒中心稳健估计算法．首先利用方位多通道回波的时域特性，建立了通道相位偏差基于多普勒中心的数学表达式；然后基于通道相位偏差会降低多普勒带宽内信号的事实，以最大化多普勒谱带宽内信号为优化准则，能够有效地估计多普勒中心．实测和仿真数据结果表明，与空间互相关系数法相比，这种算法具有相近的精度，并且在通道空间欠采样时表现更加稳健．

合成孔径雷达;多普勒中心;多通道

在方位多通道高分辨宽测绘带合成孔径雷达(High-Resolution Wide-Swath Synthetic Aperture Radar，HRWS SAR)处理中，数字波束形成技术能够有效地抑制多普勒模糊，同时实现宽测绘带和高分辨成像[1-2]．在实际中，由于加工工艺、温度等因素的影响，各接收通道间通常存在幅相特性误差，这将会大大降低多普勒解模糊性能．针对通道相位偏差校正问题，国内外提出了很多行之有效的通道间相位偏差估计算法[3-6]，但现有算法大都存在以下限制: 在频域估计算法中，多普勒中心往往要求精确已知，否则会降低算法精度; 在时域估计算法中，多普勒中心作为重要的中间变量，其误差会导致相位偏差估计中出现线性误差[3]．另一方面，多普勒中心也是合成孔径雷达成像聚焦的重要参数之一．然而，在方位多通道合成孔径雷达系统中，由于存在方位欠采样和通道相位偏差，传统的方位互相关系数法[7]已经无法准确估计回波多普勒中心，因此研究多普勒中心估计具有相当重要的意义．

文献[8]提出了利用拉东变换来计算多普勒中心，尽管该算法能够同时求解多普勒模糊数和多普勒中心，但仍然存在运算量大和精度低的问题．相比之下，文献[3]提出的空间互相关系数算法能快速准确地估计基带多普勒中心，但其要求系统通道满足空间过采样，这对于雷达系统设计带来了一定的限制．

笔者首先简要介绍了方位多通道回波信号模型，然后分别从频域和时域分析了多普勒中心、通道相位偏差以及回波多普勒谱的联系．分析表明，多普勒中心偏差将在时域通道相位偏差估计中引入线性误差，继而会降低重构多普勒带宽内的频谱能量．基于上述分析，笔者提出一种新的方位多通道回波多普勒中心稳健估计算法．该算法利用了相邻通道的干涉信息，以多普勒中心表示通道相位偏差，通过优化多普勒频谱使得多普勒带宽内能量最大，从而能有效地估计多普勒中心．

1 信号模型

(1)

将所有通道回波信号以矢量形式表示，则有

由式(2)可知，多普勒重构后的无模糊信号可写为

2 算法原理

在方位多通道合成孔径雷达系统中，相邻通道接收的回波数据之间具有良好的相干性[4]．同一时刻相邻通道回波的互相关系数可表示为[3]

其中，Δφm，m-1=φm-φm-1，Δtm，m-1=Δtm-Δtm-1，Rs0表示s0的互相关函数，上标*表示共轭操作．

通过累乘所有相邻通道的互相关系数，进一步可得

(16)

将式(16)代入式(10)，无模糊的回波信号可通过下式估计:

(17)

(18)

图1 多普勒带宽内频谱能量随多普勒中心频率偏差的变化曲线

基于上述分析，笔者提出了以最大化多普勒带宽Ba内的信号为准则的多普勒中心频率估计方法，其数学表达如下:

其中，F(fdc)为待优化的代价函数．wl(fd) 是位于fd+(k0+l-1)fPR处频谱分量的加权值:

(21)

上述优化问题的求解过程可利用牛顿迭代法实现[5， 9-11]．第k+1次迭代中的多普勒中心频率估计值fk+1如下:

在计算过程中，迭代初值f0可通过系统参数及轨道信息来计算．笔者提出的算法联合了信号的时域信息和频域信息，使迭代过程中未知参数仅有多普勒中心频率一项，从而具有易于收敛和估计稳健的优势．值得一提的是，利用式(16)，笔者提出的算法能在估计多普勒中心频率的同时得到各通道的相位偏差．

3 实验结果分析

3.1 有效性验证

为了验证笔者提出算法的有效性，采用了机载X波段方位四通道实测数据．4个接收通道在方位向上等间隔分布，主要系统参数如表1所示．各通道原始回波数据均满足奈奎斯特采样，因此采用平均相关系数算法估计各通道原始数据的多普勒中心频率作为参考，其结果分别为 2.3 Hz、2.7 Hz、2.2 Hz 和 2.0 Hz．为获得方位模糊的多通道数据，对原始数据在方位向进行了5倍降采样，即新的脉冲重复频率为 100 Hz．

表1 主要系统参数

对于按照上述步骤得到的多通道数据，分别使用空间互相关系数法和文中算法估计多普勒中心频率，其中笔者提出的算法迭代次数为3次．空间互相关系数法的估计结果为 2.35 Hz， 而笔者提出的算法估计结果为 2.32 Hz．通过对比可知，两种算法的估计结果均和单通道原始数据的估计结果吻合，这表明两种算法均能准确地估计多普勒中心频率．利用笔者提出的算法同时可得各通道间相位偏差0°，-19.83°，38.02°，-32.26°，然后分别对通道相位偏差校正前后的数据进行多普勒解模糊成像，结果如图2所示．图2(a)是通道1无模糊原始回波的成像结果，图2(b)和图2(c)分别是多普勒中心频率估计及通道相位偏差校正前后的多通道数据成像结果．与图2(a)相比，图2(b)中明显出现了由于方位模糊引起的虚假目标，尤其是在圆圈标注的区域．而相比于图2(b)， 经过估计校正后的图2(c)中方位模糊得到了很好的抑制．该现象说明利用笔者提出的算法获得的相位偏差具有较高的准确性，这也从侧面验证了笔者提出的算法多普勒中心频率估计结果的准确性．综上所述，笔者提出的算法能够有效准确地估计多普勒中心频率和通道相位偏差．

图2 笔者提出的算法估计校正前后的多通道成像结果对比

3.2 性能对比分析

对笔者提出的算法和空间互相关系数法的性能进行对比实验，实验中采用了一组方位多通道合成孔径雷达仿真数据，4个接收通道(通道1至通道4)在方位向上等间隔分布，其系统参数如表2所示．这里引入了文献[4]中定义的通道均匀因子，即Fu=Md/ (V/fPR)，其中M、d、V和fPR分别代表方位多通道系统中的通

表2 仿真数据系统参数

道数目、通道方位间距、平台速度和脉冲多普勒频率．通道均匀因子越接近1，代表各通道的采样位置越接近均匀采样．实验中，首先通过方位重采样获得了不同fPR的多通道数据，即不同Fu下的仿真数据; 接下来，通过蒙特卡罗仿真对比了信噪比为 10 dB 时两种算法在不同Fu下的估计精度，试验次数为 1 000 次．不失一般性，实验中采用多普勒中心频率估计值的均方根误差σ评价多普勒估计精度:

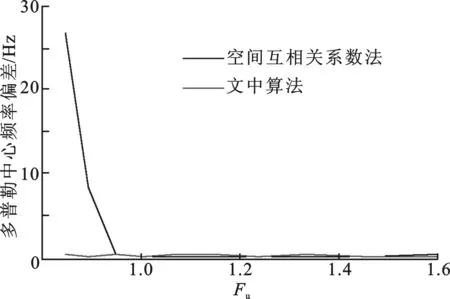
图3 多普勒中心频率估计精度随通道均匀因子Fu的变化曲线

(24)

4 结 束 语

基于多普勒中心频率对相位偏差以及重构频谱带宽内信号能量的影响，笔者提出了一种新的方位多通道系统多普勒中心频率估计算法．该算法利用了相邻通道的干涉信息，以多普勒中心频率表示通道相位误差，通过优化多普勒频谱使得多普勒带宽内能量最大，从而有效地估计多普勒中心频率．实验结果验证了笔者提出算法的有效性．与空间互相关系数法相比，笔者提出的算法具有相近的精度，且在通道空间欠采样时表现得更加稳健．

参考文献：

[1] KRIEGER G, GEBERT N, MOREIRA A. Unambiguous SAR Signal Reconstruction from Nonuniform Displaced Phase Center Sampling[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(4): 260-264.

[2] LI Z F, WANG H Y, SU T, et al. Generation of Wide-swath and High-resolution SAR Images from Multichannel Small Spaceborne SAR Systems[J]. IEEE Geoscience and Remote Sensing Letters, 2005, 2(1): 82-86.

[3] LIU Y Y, LI Z F, WANG Z B, et al. On the Baseband Doppler Centroid Estimation for Multichannel HRWS SAR Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(12): 2050-2054.

[4] LIU Y Y, LI Z F, YANG T L, et al. An Adaptively Weighted Least Square Estimation Method of Channel Mismatches in Phase for Multichannel SAR Systems in Azimuth[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(2): 439-443.

[5] FANG C, LIU Y Y, LI Z F, et al. Clutter-cancellation-based Channel Phase Bias Estimation Algorithm for Spaceborne Multichannel High-resolution and Wide-swath SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(9): 1260-1264.

[6] WANG Z B, LIU Y Y, LI Z F, et al. Phase Bias Estimation for Multi-channel HRWS SAR Based on Doppler Spectrum Optimization[J]. Electronics Letters, 2016, 52(21): 1805-1807.

[7] MADSEN S N. Estimating of the Doppler Centroid of SAR Data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 25(2):134-140.

[8] KONG Y K, CHO B L, KIM Y S. Ambiguity-free Doppler Centroid Estimation Technique for Airborne SAR Using the Radon Transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 715-721.

[9] XU G, XING M D, XIA X G, et al. Sparse Regularization of Interferometric Phase and Magnitude for InSAR Image Formation Based on Bayesian Representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2123-2136.

[10] 张榆红, 邢孟道. 联合的平动和转动相位自聚焦方法[J]. 西安电子科技大学学报, 2016, 43(5): 31-35.

ZHANG Yuhong, XING Mengdao. TDOA Location Algorithm Based on Modified Newton Iterations[J]. Journal of Xidian University, 2016, 43(5): 31-35.

[11] 房嘉奇, 冯大政, 李进. TODA中的修正牛顿及泰勒级数方法[J]. 西安电子科技大学学报, 2016, 43(6): 27-33.

FANG Jiaqi, FENG Dazheng, LI Jin. Research on Modified Newton and Taylor-series Methods in TDOA[J]. Journal of Xidian University, 2016, 43(6): 27-33.

RobustDopplercentroidestimationmethodformultichannelHRWSSAR

FANGChao1，LIUYanyang2，LIZhenfang1，RENWei2，CHENJunli3

(1. National Key Lab. of Radar Signal Processing, Xidian Univ., Xi’an 710071, China; 2. Shanghai Institute of Satellite Engineering, Shanghai 201109, China; 3. Shanghai Academy of Space Technology, Shanghai 201109, China)

In multichannel high-resolution and wide-swath(HRWS) synthetic aperture radar(SAR) systems, a novel method for the Doppler centroid estimation is proposed. First, by exploiting temporal characteristics of multichannel SAR data, mathematical expressions for channel phase biases on the Doppler centroid are established. Second, based on the fact that phase biases decrease the signals inside the Doppler bandwidth, the Doppler centroid could be estimated by maximizing the energy inside the Doppler bandwidth. Experimental results show that the proposed method has an estimation accuracy similar to that of the spatial cross-correlation coefficient method but has more robustness.

synthetic aperture radar; Doppler centroid; multichannel

2017-01-13

时间：2017-06-29

国家自然科学基金资助项目(61471276，41371439, 61601298, 61671355)

房 超(1989-)，男，西安电子科技大学博士研究生，E-mail：fangc61147@163.com．

http://kns.cnki.net/kcms/detail/61.1076.TN.20170629.1734.012.html

10.3969/j.issn.1001-2400.2018.01.006

TN957

A

1001-2400(2018)01-0030-05

(编辑： 郭 华)