机器学习模型 在河北省参考作物蒸散量计算中的比较

张 薇，霍树义，贾 悦

(1. 河北省南运河河务管理处，河北 沧州 061001；2. 河北水利电力学院，河北 沧州 061001)

0 引 言

作物蒸散量(Crop Evapotranspiration，ET)是水文循环中的重要参数，合理精确的计算农田ET，对当地灌溉制度的建立有着至关重要的作用[1]。目前，双作物系数法是精确计算作物蒸散量的主要方法之一，其计算精度已得到了广泛的验证[2]。参考作物蒸散量(reference crop evapotranspiration，ET0)是双作物计算法计算ET的主要参数之一，其正确估算是正确计算ET的前提。目前针对ET0的计算方法主要分为辐射法、温度法和综合法3大类[3]，而1998年FAO-56分册规定Penman-Monteith(P-M)公式因其考虑因素较全面，可作为ET0计算的标准方法使用[4]。但由于P-M公式计算复杂，需要的气象资料较多，在资料缺失的地区应用受限，因此ET0简化算法一直是近年来国内外研究的热点。Hargreaves公式仅靠温度资料即可较精确地得出ET0，但其适用范围不同，其计算值普遍高于P-M公式计算值[5]。机器学习模型由于其计算原理简单、计算精度较高，现已普遍应用于ET0精确估算当中，本文在河北省利用极限学习机模型(ELM)和广义回归神经网络模型(GRNN)，仅用温度资料建立ET0估算模型，并以P-M公式为标准，与Hargreaves公式进行比较，得出适用于河北省ET0计算的精确模型，以期为当地水资源决策的制定提供理论依据。

1 研究区域概况与研究方法

1.1 研究区域概况

河北省(36°01′～42°37′N，113°04′～119°53′E)地处华北平原，属温带大陆性季风气候，地形西北高、东南低，多年平均降水量531.7 mm，本研究采用包括石家庄、保定在内的7个气象站点1961-2015年的逐日气象资料，数据来自国家气象信息中心，质量良好，本文拟采用1961-2005年的数据训练机器学习模型，采用2006-2015年的数据验证模型精度，站点具体分布图见图1。

图1 河北省气象站点分布图

1.2 研究方法

1.2.1 Penman-Monteith公式与Hargreavves公式

1998年FAO-56分册推荐的Penman-Monteith(P-M)公式具有较完备的理论依据和较高的计算精度，在世界范围内得到广泛使用。20世纪50年代 Hargreaves和Samani共同提出基于温度和辐射计算ET0的方法Hargreaves(H-S)公式，具体计算公式见文献[5]中的详细描述。

1.2.2 极限学习机(ELM)模型

ELM模型可以很好地克服传统神经网络收敛速度慢的缺点，在回归检验、模型预测领域已得到了极大的应用。图2为ELM模型的基本原理图，ELM模型主要可分为输入层、隐含层和输出层3部分。首先通过输入层输入所求变量，通过与隐含层之间的权重ωij，计算出输出层权重βjk和输出变量矩阵，得出最终结果。本文中ELM模型算法采用Matlab2013a软件进行模拟计算，详细运算过程与代码形式见参考文献[6]。

图2 ELM模型计算原理图

1.2.3 广义回归神经网络(GRNN)模型

GRNN模型具有较强的非限制性映射能力，可依据概率最大原则模拟计算数据[6]。主要包括输入层、模式层、求和层和输出层4个步骤，利用Matlab软件调用广义神经网络模型函数进行计算。

1.2.4 模型评价指标体系建立

Nash-Sutcliffe系数CD、逐日相对均方根误差(RMSE)和Kendall一致性系数K是可反映数据误差与一致性的数据评价指标体系。其中，CD与K的值越大、RMSE的值越小，模型算法与实测值的一致性越好、计算精度越高，具体公式如下：

(1)

(2)

(3)

2 结果与分析

2.1 ET0日值精度对比

图3为石家庄站不同模型ET0模拟结果日值精度对比(由于篇幅限制，其余站点结果见表1)。不同站点ET0日值模拟结果均呈现机器学习模型显著高于H-S模型的情况。H-S模型不同站点拟合方程的斜率均在1.60以上，在秦皇岛站达到了1.863，表明H-S模型明显高估了ET0的模拟值，而GRNN模型和ELM模型的ET0日值拟合方程斜率均在0.90～1.10之间，表明机器学习模型与P-M模型的ET0日值计算结果精度较高，不同模型计算值的决定系数R2差别不大，且相关性均达到了极显著水平(P<0.01)，综上所述，机器学习模型对ET0日值模拟精度明显高于H-S模型。

图3 石家庄站不同模型模拟ET0日值精度对比

站点H-S模型拟合方程R2GRNN模型拟合方程R2ELM模型拟合方程R2石家庄y=1．640x-0．1380．809∗∗y=0．923x-0．1380．809∗∗y=0．979x+0．3630．786∗∗保定y=1．688x-0．1880．800∗∗y=0．958x-0．0070．812∗∗y=1．006x+0．3020．802∗∗张家口y=1．619x-0．6820．779∗∗y=0．961x-0．4380．795∗∗y=1．010x-0．1830．814∗∗秦皇岛y=1．863x-0．5280．714∗∗y=0．831x-0．0870．785∗∗y=0．922x+0．1680．812∗∗邢台y=1．640x+0．0580．802∗∗y=0．932x+0．1410．807∗∗y=0．978x+0．4640．802∗∗承德y=1．803x+0．0830．830∗∗y=1．078x+0．0480．776∗∗y=1．028x+0．3210．807∗∗唐山y=1．769x-0．4290．796∗∗y=0．931x-0．0630．777∗∗y=0．997x+0．2070．973∗∗

2.2 ET0月值精度对比

不同站点不同模型ET0年内分布如图4所示。图4显示，各站点不同模型ET0变化趋势基本一致，呈开口向下的二次抛物线形势。春季和冬季的ET0相对较小，夏季ET0值相对较大。各站点ET0在6月份达到最大值；在1月、12月各站点ET0值最小，均小于1.0 mm/d。1-7月，各站ET0基本呈线性增长的趋势，9-12月，各站点ET0下降趋势显著。由图4中可以看出，H-S模型计算结果明显高于其余模型，尤其在6月份，各站点H-S模型计算结果较P-M模型提高了51.3%～75.6%，而GRNN模型与ELM模型较P-M模型结果最高相差18.2%，可以明显看出，GRNN模型与ELM模型的计算精度明显高于H-S模型。

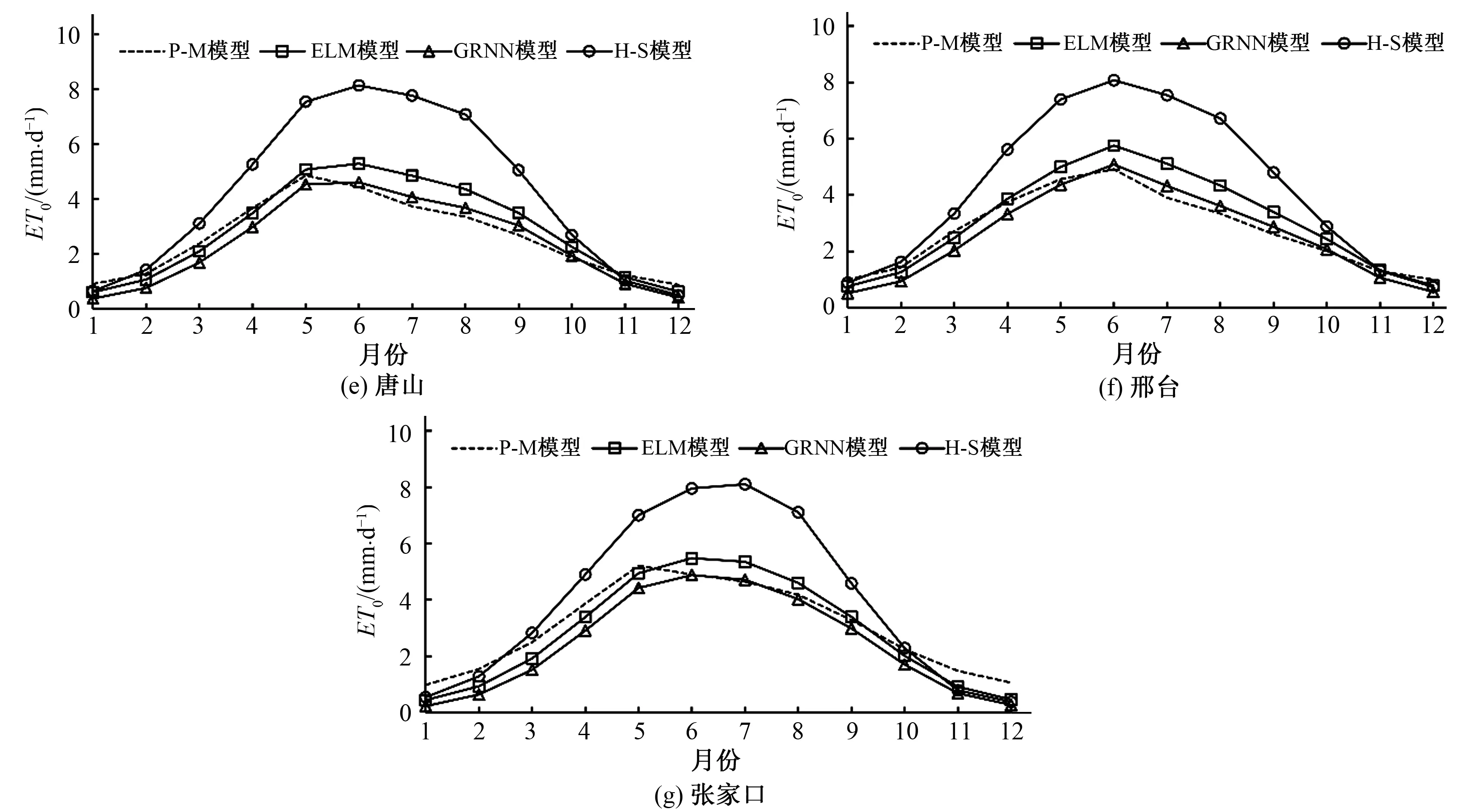
图4 不同站点不同模型ET0精度年内分布

2.3 ET0精度指标对比

不同站点不同模型ET0精度指标计算结果见表2。表2显示，在不同站点H-S模型的计算误差明显高于GRNN模型和ELM模型，不同站点H-S模型的RMSE值均在0.50以上，而GRNN模型的RMSE值均在0.30以下，ELM模型的RMSE值更是低于0.25，这表明机器学习模型的计算精度明显高于H-S模型，同时ELM模型的计算精度要高于GRNN模型；对不同模型的一致性指标进行计算可以发现，H-S模型在不同站点的CD与K值均在0.70以下，且仅在张家口、秦皇岛、石家庄站，相关性达到了显著水平(P<0.05)，其余站点均不显著，而GRNN模型与ELM模型的C与K值均在0.75以上，且GRNN模型在张家口、承德站的CD值达到了0.90以上，且相关性均达到了极显著水平(P<0.01)，这表明3种模型与P-M模型计算结果的一致性表现为GRNN >ELM >H-S模型。

表2 不同模型ET0精度指标对比

2.4 ET0空间精度对比分析

图5为不同模型计算结果与P-M模型计算结果相对误差的空间分布对比。图5显示，不同模型计算精度在河北省的分别基本呈现出由西南到东北，相对误差逐渐提高的趋势，其中，GRNN模型与ELM模型在整个河北省的计算精度明显高于H-S模型，GRNN模型在承德站的计算精度最低，相对误差为13.45%，而ELM模型在秦皇岛站的相对误差最高，达到了31.47%，而H-S模型在整个河北省计算结果的相对误差均在25.74%以上，在承德和秦皇岛站附近，相对误差分别达到了69.37%和71.40%，综上所述，机器学习模型在整个河北省的计算精度要明显高于H-S模型。

3 结 论

本文通过模拟ELM模型和GRNN模型2种机器学习模型的ET0计算结果，在仅适用温度资料的前提下，与H-S模型进行了比较，得出了以下结论：不同站点ELM模型与GRNN模型的ET0日值拟合方程斜率更接近于1，且ET0月值计算结果与P-M模型计算结果最为接近，对不同模型计算结果精度指标进行比较可知，3种模型RMSE值表现为GRNN < ELM ELM>H-S模型，表明在河北省ET0的计算中，机器学习模型的计算精度要高于H-S模型，其中GRNN模型为精度最高的模型，可作为河

图5 不同站点不同模型ET0相对误差空间分布

北省ET0简化计算的标准模型使用。

参考文献：

[1] 黄 垚，王景雷，孙景生，等. 作物蒸散不同时空尺度模型及尺度转换方法研究进展[J]. 中国农业通报，2013，29(21)：23-26.

[2] 卢晓鹏，段顺琼，马显莹，等. 单双作物系数法计算玉米需水量的对比研究[J]. 节水灌溉，2012，(11)：18-21.

[3] 贾 悦，崔宁博，魏新平，等. 基于反距离权重法的长江流域参考作物蒸散量算法适用性评价[J]. 农业工程学报，2016，32(6)：130-138.

[4] Allen R G, Pereira L S, Raes D, et al. Crop evapotranspirationguidelines for computing crop water requirements[M]. Rome: Food and Agriculture Organization of United Nation, 1998.

[5] 胡庆芳，杨大文，王银堂，等. Hargreaves公式的全局校正及适用性评价[J]. 水科学进展，2011，22(2)：160-167.

[6] 王小川，史 峰，郁 磊，等. MATLAB 神经网络43个案例分析[M]. 北京：北京航空航天大学出版社，2013：243-255．