酉不变范数下{1,3}-和{1,4}-逆的扰动界

孟令胜

(西北师范大学 数学与统计学院， 甘肃 兰州 730070)

0 引 言

广义逆理论是一个应用十分广泛的数学分支，在数值线性代数、线性规划、最优化、控制论、马尔可夫链、数理统计、信号传输、微分方程等重要领域都有极其广泛的应用. 1955年PENROSE在MOORE关于广义逆的基础上提出了4个更加便于理解的方程[1]：

设A∈Cm×n，若存在G∈Cn×m使得

(1)AGA=A; (2)GAG=G;

(3) (AG)*=AG; (4) (GA)*=GA,

则称G是A的Moore-Penrose逆，这4个方程称为M-P方程.

全部或部分满足M-P方程的矩阵G，称为A的广义逆. 若G满足M-P方程中的第(i),…,(j)个方程，则称G为矩阵A的一个{i,…,j}-逆，记为A{i,…,j}.A的所有{i,…,j}-逆的集合用A{i,…,j}表示，其中A{1},A{1,2},A{1,3}和A{1,4}都是常用的广义逆，并且一般都不是唯一存在的.

广义逆的扰动研究是广义逆理论中一个非常重要的课题，WEDIN[2]、STEWART[3]、孙继广[4]和WEI等[5]等国内外专家都在此研究领域做出了重要贡献. 迄今为止，广义逆扰动理论的研究成果已有很多. 关于Moore-Penrose逆和Drazin逆的扰动理论可参阅文献[1-12].

鉴于{1}-逆在矩阵理论和计算中的重要作用(例如相容线性系统Ax=b的通解可以表示为x=A(1)b+(I-A(1)A)y)，LIU等[12]研究了{1}-逆在保秩扰动下的连续性；WEI等[13]和MENG等[14]分别给出了{1}-逆在谱范数和Frobenius范数下的加法和乘法扰动界. 另外， 因为{1,3}-和{1,4}-逆在实际应用中也起着非常重要的作用，例如最小二乘问题min‖Ax-b‖2的最小二乘解可表示为x=A(1,3)b；相容线性系统Ax=b的最小范数解可表示为x=A(1,4)b[1]，所以MENG等[14]研究了这两类广义逆在谱范数和Frobenius范数下的加法和乘法扰动界.

因谱范数和Frobenius范数是两类特殊的酉不变范数，因此，本文试图将文献[14]中的关于{1,3}-和{1,4}-逆在谱范数和Frobenius范数下的结果推广到一般的酉不变范数. 对于给定的矩阵A,B∈Cm×n及A(1,i)∈A{1,i},i=3,4，文献[14]给出了谱范数和Frobenius范数下距离A(1,i)最近的矩阵B的{1,i}-逆的具体表达式，参见文献[14]theorem 3.1和theorem 3.2.

本文的主要工作为： 首先证明当谱范数和Frobenius范数推广到一般的酉不变范数时，文献[14]中给出的距离A(1,i)最近的矩阵B的{1,i}-逆不变；其次，利用该结果给出{1,3}-和{1,4}-逆在酉不变范数下的加法和乘法扰动界，所得扰动界推广和改进了文献[14]中的结果.

首先给出本文所用到的2个引理.

其中L,M为适当阶数的矩阵.

引理2[14]设矩阵X,Y∈Cm×n，如果X*Y=0，则‖X‖≤‖X+Y‖.

1 最佳逼近的{1,3}-和{1,4}-逆

其中i=3,4.

定理1假设A,B∈Cm×n. 对于任意给定的A(1,3)∈A{1,3},存在唯一的矩阵

使得

‖B+-B+BA(1,3)‖.

(1)

‖B(1,3)-A(1,3)‖.

且

因此

‖B+-B+BA(1,3)‖,

其中，

证毕.

注意到当且仅当G*∈A*{1,3}时,G∈A{1,4}，因此利用上述定理中的结果，容易得到下面的定理.

定理2假设A,B∈Cm×n. 对于任意给定的A(1,4)∈A{1,4}，存在唯一的矩阵：

使得

‖B+-A(1,4)BB+‖.

注记1当定理1和定理2中的酉不变范数取为谱范数或Frobenius范数时，定理1和定理2中的结果就分别变成文献[14]中的theorem 3.1和theorem 3.2.

2 {1,3}-和{1,4}-逆的加法和乘法扰动界

利用上节结果，本节将给出 {1,3}-和{1,4}-逆的加法和乘法扰动界.

‖A+‖2‖BB+E‖2‖A(1,3)‖+O(‖E‖2‖E‖).

证明对于给定的A(1,3)，由引理1知，存在矩阵Z∈Cn×m，使得A(1,3)=A++(I-A+A)Z. 另外，易见

B+-A+=B+(A-B)A++B+(I-AA+)-

(I-B+B)A+.

(2)

故由式(1)、(2)及B=A+E可得

‖-B+EA+-B+E(I-A+A)Z‖+

‖B+BB+(I-AA+)‖=‖B+BB+EA(1,3)‖+

‖B+(B+)*E*(I-AA+)‖≤

‖B+‖2‖BB+E‖2‖A(1,3)‖+

另外,由定理的条件知:

从而可推得结论成立.证毕.

其中，Φ(D1,D2)=(1-‖I-D1‖2)(1-‖I-D2‖2)，且t1和t2为任意复数.

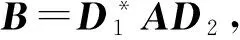
(3)

当max{‖I-D1‖2, ‖I-D2‖2}<1时，有

(4)

对于给定的A(1,3)，由引理1知，存在矩阵Z∈Cn×m，使得A(1,3)=A++(I-A+A)Z.

综合式(2)和(3)，得到

B+-B+BA(1,3)=B+B(B+-A+-(I-A+A)Z)=

由上式和式(4),可得

‖B+-B+BA(1,3)‖≤

证毕.

再次利用G∈A{1,4}当且仅当G*∈A*{1,3}，由定理3和定理4即得{1,4}-逆的加法和乘法扰动界：

‖A+‖2‖EB+B‖2‖A(1,4)‖+O(‖E‖2‖E‖).

max{‖I-D1‖2, ‖I-D2‖2}<1，则有

其中，Φ(D1,D2)=(1-‖I-D1‖2)(1-‖I-D2‖2)，t1和t2为任意复数.

注记2当定理3和定理5中的酉不变范数取为谱范数或Frobenius范数时，定理3和定理5就是文献[14]中的theorem 4.1；当定理4和定理6中的酉不变范数取为谱范数或Frobenius范数且t1=t2=1时，定理4和定理6就变为文献[14]中的theorem 5.2. 另外，注意到定理4和定理6给出的扰动界对任意复数t1和t2都成立，从而改进了文献[14]的结果.

参考文献(References)：

[1] BEN-ISRAEL A, GREVILLE T N E.GeneralizedInverses：TheoryandApplications[M]. 2nd ed. New York: Springer, 2003.

[2] WEDIN P Å. Perturbation theory for pseudoinverse [J].BIT, 1973, 13 (2) ： 217-232.

[3] STEWART G W. On the perturbation of pseudo-inverses, projections, and linear least squares problems [J].SIAMReview, 1977, 19 (4) ： 634-662.

[4] 孙继广.矩阵扰动分析[M].第2版. 北京： 科学出版社，2001.

SUN J G.MatrixPerturbationAnalysis[M]. 2nd ed. Beijing： Science Press, 2001.

[5] WEI Y, LI X, BU F. A perturbation bound of the Drazin inverse of a matrix by separation of simple invariant subspaces [J].SIAMJournalonMatrixAnalysisandApplications, 2005, 27 (1)： 72-81.

[7] HU N, LUO W, SONG C, et al. Norm estimations for the Moore-Penrose inverse of multiplicative perturbations of matrices [J].JournalofMathematicalAnalysisandApplications, 2016, 437(1)： 498-512.

[8] CAI L, XU W, LI W. Additive and multiplicative perturbation bounds for the Moore-Penrose inverse [J].LinearAlgebraanditsApplications, 2011, 434： 480-489.

[9] MENG L, ZHENG B. The optimal perturbation bounds of the Moore-Penrose inverse under the Frobenius norm [J].LinearAlgebraanditsApplications, 2010, 432(4)： 956-963.

[10] MENG L, ZHENG B. New multiplicative perturbation bounds of the Moore-Penrose inverse [J].LinearandMultilinearAlgebra, 2015, 63 (5) ： 1037-1048.

[11] ZHANG P, YANG H. A note on multiplicative perturbation bounds for the Moore-Penrose inverse [J].LinearandMultilinearAlgebra, 2014, 62 (6) ： 831-838.

[12] LIU X, WANG W, WEI Y. Continuity properties of the {1}-inverse and perturbation bounds for the Drazin inverse [J].LinearAlgebraanditsApplications, 2008, 429： 1026-1037.

[13] WEI M, LING S. On the perturbation bounds of g-inverse and oblique projections [J].LinearAlgebraanditsApplications, 2010, 433： 1778-1792.

[14] MENG L, ZHENG B, MA P. Perturbation bounds of generalized inverses [J].AppliedMathematicsandComputation, 2017, 296： 88-100.