在美国破产保护法第十一章下公司债券的定价和最佳破产边界研究
2018-05-08林建伟
林建伟
(莆田学院 数学与金融学院, 福建 莆田 351100)
公司债券定价是金融研究的热门问题之一. 1974年MERTON[1]首次提出结构化方法对零息票公司债券进行定价. MERTON的工作具有开创意义,但存在信用利差估计偏低的问题. 为了弥补这一不足,1976年BLACK等[2]提出通过时间模型对公司债券进行定价;1994年LELAND[3]利用结构化方法对具有内生破产边界的永久付息票公司债券进行定价;2009年CHEN等[4]在双指数跳扩散模型下,采用随机分析方法对永久公司债券进行定价. 上述文献的研究结果都是在美国破产保护法第七章下获得的,即公司一旦宣布破产,立即被清算,视破产等同于清算,不考虑破产重组的可能,这与市场的实际情况不符. 事实上,公司一旦宣布破产,将有权借助于美国破产保护法第十一章获得一段额外的破产保护期,以便公司进行资产重组. 若公司在破产保护期内通过有效资产重组计划,使公司成功摆脱困境,则公司将继续正常经营;否则宣布破产的公司将在美国破产保护法第七章下被清算. 1996年,ANDERSON等[5]提出策略债务支付的重组策略,通过展开型博弈规则确定策略债务支付的息票数额,利用二叉树方法对有限到期日公司债券进行定价,其不足是未对美国破产法第十一章进行系统的数学模型刻画;2000年FAN 等[6]分别从最佳破产边界的选取标准、破产保护期门槛的界定、资产重组策略规定和破产价值四方面对美国破产法第十一章进行了系统的数学模型刻画,采用常微分方程法对具有无限破产保护期和无限到期日公司债券进行定价;2004年FRANCOIS等[7]推广了FAN等的工作,采用随机分析方法,对具有有限破产保护期和无限到期日公司债券进行定价;2008年林建伟[8]通过偏微分方程法将FRANCOIS等的模型结果推广至考虑公司在破产保护期内策略债务支付息票的数额;但上述研究仅考虑公司永久债券连续,其数学模型与市场不符,在有限到期日公司债券定价上较稳态情形困难. 此时,公司债券和股票的价值不仅依赖于公司的资产价值,还依赖于距离到期日的时间长度,相应的最佳破产边界也是一条随时间变化的曲线. 2007年BROADIE等[9]假定最佳破产边界具有参数函数形式,即最佳破产边界为初始最佳破产边界的远期,并假定在破产边界曲线和破产保护期门槛曲线相同条件下,应用二叉树方法,建立了具有有限破产保护期和有限到期日的公司债券定价的二叉树模型,获得了二叉树定价离散格式;但并没有真正对最佳破产边界进行处理,获得的破产边界也并非最佳. 意识到这一点,2013年DAI等[10]基于BROADIE等的模型,得到了区分破产边界曲线和破产保护期门槛曲线,即破产保护期门槛曲线仍假定为宣布破产时刻公司价值的远期,但最佳破产边界曲线将通过股票价值满足的最优停时问题来确定,进而通过最优停时方法和技巧建立具有有限破产保护期和有限到期日的公司债券定价的连续模型,并通过离散惩罚函数获得定价问题的数值解. 由于在该模型下,公司宣布破产后其总价值满足三维抛物型方程组,在理论上进一步刻画最佳破产边界的性质具有相当的难度,故仅通过数值计算分析最佳破产边界曲线的性质,而不是从理论上对最佳破产边界的存在唯一性和单调性进行严格的数学证明,也没有讨论公司在破产保护期内策略债务支付息票数额的大小.
与文献[10]的模型相同,本文将通过股票价值满足的最优停时问题来区分破产边界曲线、破产保护期门槛曲线和最佳破产边界曲线. 不同的是,破产保护期门槛将按照FAN等[6]的模型进行界定,即假定公司宣布破产,公司股东和债权人为摆脱公司困境,将对资产进行重组,双方将对收益进行调整,即一方面规定在破产保护期内公司停止或少支付债权人按合约规定的息票数额,另一方面将公司债券转化为一张永久性债券,到期不需要支付本金. 将破产保护期门槛转化为不依赖于时间变化的常数. 在该假定下,本文首先采用结构化方法和最优停时技巧,建立具有有限破产保护期和有限到期日公司债券定价的连续数学模型,然后通过偏微分方程理论和方法,严格证明了最佳破产边界的存在唯一性和单调性, 得到了公司在破产保护期内策略债务支付息票数额的解析表达式. 最后基于数值计算,分析了美国破产保护法第十一章对公司债券和股票价值以及最佳破产边界的影响.
1 基本假定
1) 市场无套利且市场是完备的.
2) 公司发行股票E与公司债券D,债券到期日为T,到期本金为P,规定债权人在公司宣布破产之前可获得单位时间CP元的息票收益,同时公司获得税盾收益,即企业通过发行公司债券获得的单位时间税盾收益为γCP,γ∈(0,1)表示企业税率;股东按红利获得收益.
3) 在概率空间(Ω,Ft,F,Q)下,公司资产价值Vt服从标准几何布朗运动方程:
其中,Q表示风险中性测度,r为无风险利率,δ为公司总的现金支付率,σ为波动率,{Wt,t≥0}表示一个标准的布朗运动.
4) 公司有权在任意时刻τ∈[0,T]宣布破产,且对任一给定破产时刻τ,Vτ为破产时刻公司资产价值,公司将通过申请美国破产保护法第十一章获得一段额外的破产保护期G,以便进行资产重组. 最佳破产边界的选取标准为股票价值最大化.
5) 清算损失率为α∈[0,1],谈判费用比例0≤φ≤δ(实际情况中,谈判费用较少,以确保公司借助资产重组获得额外收益).
6) 资产重组策略的规定: 当公司在任一时刻τ宣布破产后,Vτ为破产时刻相应的资产价值,公司的股东和债权人通过以下策略共同决定进行资产重组,即宣布破产后,公司债券转化为永久债券,到期不需要支付本金P,同时规定,当Vt 根据上述基本假定6)中关于资产重组策略的规定,对于任一时刻τ公司宣布破产后,Vτ为相应破产时刻公司资产价值,在给出公司股票和债券的定价模型之前,首先考虑公司总价值的数学模型和定价公式. 记 gt=t-sup{0≤s≤t:Vs≥Vτ}, 其中,gt表示在t时刻之前公司资产价值在破产边界Vτ以下徘徊的时间,β表示公司最终因gt=G而被清算的时刻. (1) 式(1)表示公司的总价值由公司从t时刻开始直到清算期间所产生的现金流的贴现现值和在清算时刻剩余的公司资产价值(清算时刻的公司资产价值扣除由清算所带来损失)的贴现现值两部分组成. 第一部分包含3项: 单位时间公司资产所产生的现金流δVs;当Vs≥Vτ时,公司获得的税盾收益为γCP; 当Vs 基于公司总价值的数学模型(1), 采用动态规划原理和偏微分方程法,可得 (2) 其中, w(x,g)= Vτ(1-α)[M1(x,g;G,a+1)-M1(-x,g;G,a+1)]- h(A;Vτ)[M1(x,g;G,a)-M1(-x,g;G,a)]+ A=-{φM3(a+1,G)Vτ+αM2(a+1,G)Vτ+ [M2(a,G)+rM3(a,G)-λ-]-1, 证明基于动态规划原理,对于任一给定破产边界Vτ,公司总价值的数学模型(1)可转化为以下具有巴黎期权特征[11-12]的定解问题: 在V=Vτ时的连接条件: 清算条件: 其中,A为待定常数, 由组合变换: (9) 其中, 记 Y(x;A,Vτ)= 则定解问题(10)~(13)可转化为标准的Cauchy问题: (14) 进而,由式(13)和(14), 可求得待定常数A. 最后由 引理1证毕. 这里θ为股东的分配比例. 由纳什均衡分配原理,最佳分配比例θ*为 即 这里η表示股东的谈判能力. 综上,当V≤Vτ时, 特别地,在任一时刻τ公司宣布破产,即V=Vτ,g=0,股东和债权人通过资产重组获得的价值分别为: (16) (17) 基于公式(2)和(15), 可求得破产保护期内策略债券支付息票数额S(V;Vτ)的显式表达式. 定理1对于任一给定的破产时刻τ,破产保护期内策略债券支付的息票数额S(V;Vτ)为 S(V;Vτ)=V[δ(1-ηα)-φ(1-η)]. (18) 表示公司宣布破产后,当Vt≥Vτ时,股东获得红利收益的贴现值; 当Vt 当0 同时由式(15),即 可得 -η(δ-φ)V+η(1-α)δV=η(φ-αδ)V, 由此可得η(φ-αδ)V=-(δ-φ)V+S(V;Vτ), 即 S(V;Vτ)=V[δ(1-ηα)-φ(1-η)]. 定理1证毕. 基于上述模型的基本假定,在风险中性测度Q下,公司股票E定价的数学模型为 E(Vt,t)= 这里κ[t,T]表示在[t,T]上所有可能宣布破产的时刻(停时),且若在[t,T]上公司没有宣布破产,则规定τ=.等式(20)表示股票价值由公司宣布破产之前所获得的红利收益贴现值和在破产时刻股票价值的贴现值组成,其中等式右边第3项表示: 若公司在到期期限T内没有宣布破产,则支付本金P给债权人,公司获得V-P的收益. 在0 (21) 终值条件: E(V,T)=max{V-P,Φ(V)}. (22) 基于股票定价模型(21)和(22), 通过偏微分方程惩罚函数法证明最佳破产边界的主要性质,研究公司股票价值对部分参数的依赖关系. 引理2在区域Σ={(V,t)|0 证明 (i)为了应用偏微分方程惩罚函数方法, 定义惩罚函数βε(t),t∈R满足以下性质: βε(t)∈C 其中M为任一大于0的待定常数. 基于上述惩罚函数的定义βε(t),易得 βε(0)=-3M-rε,βε(ε)=-M-rε. (23) (ii)为了对函数max{V-P,Φ(V)}进行光滑,定义光滑化函数Πε(t),t∈R满足: Πε(t)∈C (24) 其中, 记 于是K(G)可重写为 基于引理1中a,b,λ-的表达式和M2(a,G),M3(a,G)的定义,可验证0≤C1(G),C2(G),B(G)≤1成立. 进而,由0≤φ≤δ,可证明0≤K(G)≤1. 作变量代换 (25) 公司股票价值满足的变分不等式模型(21)和(22)可转化为 (26) 基于上述惩罚函数βε(t)和光滑化函数Πε(t)的构造,定解问题(26)相应的惩罚问题为 (27) 定义 基于惩罚问题(27),计算可得 其中,ζ=ex-P-Φ(ex). 再通过惩罚问题的收敛定理[13],立得引理2结论成立. 引理3当r≥(1-γ)C时,在区域Σ上, 公司股票价值E(V,t)关于时间变量t单调递减. 由式(27)计算可得 其中, ηK(G)ex]+(γ-1)CP-βε(Πε(ζ))≥ r[Πε(ζ)+Φ(ex)]+δex+(γ-1)CP-βε(Πε(ζ)). δex+(γ-1)CP-βε(0)≥ -{ηγCP[1-B(G)]+(1-γ)CP}-βε(0). 由式(23), 选取正数 M=ηγCP[1-B(G)]+(1-γ)CP, (iii)当-ε≤ζ≤ε时,|Πε(ζ)|≤ε,0≤ ηγCP(1-B(G))+(γ-1)CP-βε(Πε(ζ))≥ -rε-[ηγCP(1-B(G))+(1-γ)CP]-βε(ε), 由式(23), 并注意到正数 M=ηγCP[1-B(G)]+(1-γ)CP, 综上,由极值原理和惩罚问题的收敛定理,可得引理3成立. 由引理2和引理3,可直接得到 其中, λ-,M2(a,G),M3(a,G)的表达式见引理1. 证明在到期日t=T,公司股票价值E(Vt,t)满足的最优停时问题(20)可简化为 因此,当Φ(V)≥V-P时,公司在T时刻宣布破产为最优,而当Φ(V) 记 显然 (i)当k1≤k2时,若 (ε>0充分小), 使得 -δV(1-ηK(G))+ηγCP(1-B(G))-(γ-1)CP> δP(k2-k1)≥0. δV(1-ηK(G))-[ηγCP(1-B(G))-(γ-1)CP]> δPk2-δPk2=0. 定理3证毕. 下面进一步分析公司股票价值E(V,t)与企业税率γ和到期日T的依赖关系. 定理4公司股票价值E(V,t)随企业税率γ单调递增,且当r≥(1-γ)C时,随到期日T递增. 证明定义 基于式(27), 直接计算可得 其中, 这里, ρ=θ2[ex-P-Φ(ex;γ1)]+ (1-θ2)[ex-P-Φ(ex;γ2)], 0≤θ1,θ2≤1. E(V,t)关于T单调递增性质是引理3结论的直接推广. 定理 4 证毕. (29) 表示债券的价值由从t时刻到公司宣布破产时刻之间的息票收益CP的现金流和在破产时刻所获得的收益这两部分的贴现值组成,而式(29)右端第3项表示: 若公司在合约期限[0,T]内无破产,则公司将在到期日获得本金收益. 其中,式(31)为终值条件,式(32)表示破产时刻债权人通过资产重组获得Ψ(V).式 (33)表示当公司资产价值趋于无穷大时,公司债券转化为一张具有相同到期日和本金的无风险公司债券. 基于公司股票价值E(V,t)满足变分不等式问题(21)、(22),首先通过偏微分方程离散的惩罚函数方法[14-15]获得股票和最佳破产边界的数值解; 然后基于公司债券满足定解问题式(30)~(33), 采用差分方法获得债券定价的数值解;进而通过与Leland模型相比较,分析股东和债权人是否可借助于美国破产保护法第十一章获得利益, 同时考察资产重组对最佳破产边界的影响. 基本参数选定为: V0=100,P=100,T=6,G=1,r=0.06, δ=0.04,σ=0.3,C=0.02,γ=0.2,φ=0.02, η=0.5,α=0.5. 注2Leland模型是在美国破产保护法第七章下的公司债券定价问题,否则,破产等同于清算. 图1 最佳破产边界关于η和φ的变化关系Fig.1 The optimal bankruptcy boundary with varying η and φ 图2 最佳破产边界关于α的变化关系Fig.2 The optimal bankruptcy boundary with varying α 图3 最佳破产边界关于G的变化关系Fig.3 The optimal bankruptcy boundary with varying G 图4 公司股票价值E(100,0)关于η和φ的变化关系Fig.4 The equity value E(100,0) with varying η and φ 图5 公司债券价值D(100,0)关于η和φ的变化关系Fig.5 The debt value D(100,0) with varying η and φ 采用结构化方法和最优停时技巧,在美国破产保护法第十一章下,建立了具有有限破产保护期和有限到期日公司债券定价的连续数学模型,获得了公司在破产保护期内策略债务支付息票数额的解析表达式,并通过偏微分方程理论和方法从理论上证明了最佳破产边界的存在唯一性和单调性,并分析了公司股票价值关于各参数的变化关系. 最后,通过偏微分方程离散惩罚函数方法获得了股票价值和相应最佳破产边界的数值解,利用差分方法获得债券价值的数值解. 数值结果表明: (1)在美国破产保护法第十一章下,公司的破产概率高于Leland 模型下的概率,较好地解释了Leland模型下公司破产概率偏低的问题. (2)股东能借助于美国破产保护法第十一章进入资产重组而获益,但债权人能否从资产重组中获益依赖于谈判因子1-η和谈判费用φ. 感谢同济大学姜礼尚教授的有益建议和指导! 参考文献(References): [1] MERTON R C. On the pricing of corporate debt: The risk structure of interest rates[J].JournalofFinance, 1974, 29(2):449-470. [2] BLACK F, COX J C. Valuing corporate securities: Some effects of bond indenture provisions[J].JournalofFinance, 1976, 31(2): 351-367. [3] LELAND H E. Corporatedebt value, bond covenants, and optimal capital structure[J].JournalofFinance, 1994, 49(4):1213-1252. [4] CHEN N, KOU S. Credit spread, optimal capital structure, and implied volatility with endogenous default and jump risk[J].MathematicalFinance, 2009, 19(3), 343-378. [5] ANDERSON R W, SUNDARESAN S. Design and valuation of debt contracts[J].ReviewofFinancialStudies, 1996, 9(1): 37-68. [6] FAN H, SUNDARESAN S. Debt valuation, renegotiation, and optimal dividend policy[J].ReviewofFinancialStudies, 2000, 13(4): 1057-1099. [7] FRANCOIS P , MORELLEC E. Capital structure and asset prices: Some effects of bankruptcy procedures[J].JournalofBusiness, 2004, 77(2): 387-411. [8] 林建伟. 具有违约观察期公司债券的定价[J].应用数学学报,2008, 31(6): 1013-1034. LIN J W. Pricing of the corporate debt with the finite default observation period[J].ActaMathematicaeApplicataeSinica, 2008, 31(6): 1013-1034. [9] BROADIE M, KAYA O. A binomial lattice method for pricing corporate debt and modeling Chapter 11 proceedings[J].JournalofFinancialandQuantitativeAnalysis, 2007, 42(2): 279-312. [10] DAI M, JIANG L S, LIN J W. Pricing corporate debt with finite maturity and Chapter 11 proceedings[J].QuantitativeFinance, 2013, 13(12):1855-1861. [11] HABER R J, SCHONBUCHER P J, WILMOTT P. Pricing Parisian options[J].JournalofDerivatives, 1999, 6(3), 71-79. [12] JIANG L.TheMathematicalModelsandMethodsofOptionPricing[M]. Singapore: World Scientific Publishing, 2005. [13] FREDMAN A.VariationalPrinciplesandFreeBoundaryProblems[M]. New York: John Wiley and Sons, 1982. [14] DAI M, KWOK Y K, YOU H. Intensity-based framework and penalty formulation of optimal stopping problems[J].JournalofEconomicDynamicsandControl, 2007, 31(12): 3860-3880. [15] FORSYTH P A, VETZAL K R. Quadratic convergence of a penalty method for valuing American options[J].SiamJournalonScientificComputation, 2002, 23(6): 2095-2123.2 在任一破产时刻τ股票和债券的价值
2.1 任一给定破产边界Vτ下公司的总价值
β=inf{s≥0:gs≥G},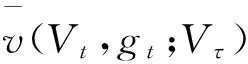

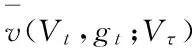

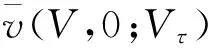
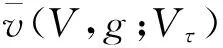


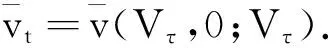
2.2 纳什均衡分配
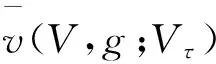
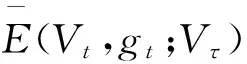



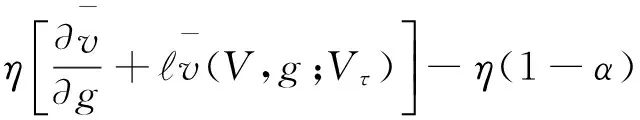
3 公司股票和债券的价值
3.1 公司股票定价的数学模型
3.2 最佳破产边界的主要性质



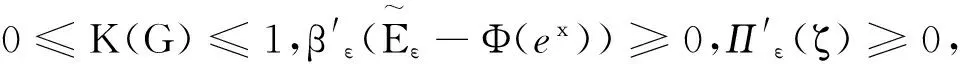

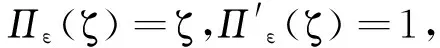





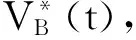
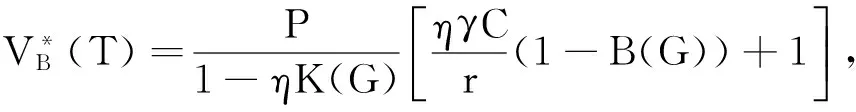







3.3 公司债券定价的数学模型

4 数值分析







5 结 论
