关于错排问题的递推公式的一点分析

冯弋舟

中图分类号：G633.6文献标识码：B文章编号：1672-1578（2018）01-0166-01

1.背景

排列组合里有一道题，叫错排问题（staggered formula）。错排问题最早被尼古拉.伯努利和欧拉研究，因此历史上也称为尼古拉.伯努利-欧拉（Bernoulli-Euler装错信封问题）。这个问题如下：写了n封信，装到n个不同的信封，每封信和信封都不匹配，问全部装错的可能性有多少种。

错排问题的标准定义是： 集合{1，2，…，n}的一个排列i1i2，…in }， 满足条件i j≠j（1≤ j≤ n），即没一个数字在它自然顺序位置的全排列。问这样的排列有多少个。n个自然数的全部错排数用Dn表示。

2.问题的提出

习题解答上在给出Dn的递推公式时，這样的：

假设i1的位置放置2（还有 3.4..n 等n-1种可能），剩下1，3，4，…n往i2，i3..in位置上放，这时错排数设为An，那么Dn=（n-1）An。An的计算又分为两种情况： （1） 1不放在第2个位置i2上，剩下n-1个数的错排数为Dn-1。（2）1放在第2个位置i2上，剩下的n-2个数的进行错排，错排数为Dn-2。所以An=Dn-1+Dn-2，所以最后总Dn=（n-1）（Dn-1 +Dn-2）。

很多刚学习错排的同学会误以为Dn-1包括Dn-2，为什么还要加Dn-2呢？

本文将分析这个问题。

3.问题分析

下面以n=4（数字小好分析）为例子分析：

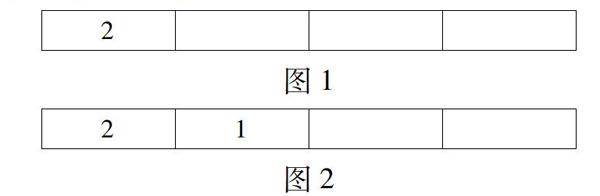
2放1位置时错排列为 2143、2341、2413，放1位置的还有3和4 ，所有共有3*3=9种错排。那么2放1位置后的剩下3个数的全错排数（图1），是否包含 2放1位置和1放2位置后的错排数（图2）呢？

把2放1位置后全错排D3，是把数字1、3、4排到第2、3、4三个位置上的错排，那么数字1、3、4 排到第2、3、4位置的错排怎么排呢？

现在把数字1、3、4改为数字"2"、3、4 在第2、3、4位置上错排，"2"（其实是1）不许排在位置2上，错排数为D3。真实情况是"2"（其实是1）是排在位置2上，也是错排，但这时的 却把这情况给排除了，所以必须加上这种情况：把数字"2"（其实是1）放在位置2上，剩下3、4两数在3、4位置上错排，错排数为D2。

所以D3不包括D2。

为什么会出现以为D3包括D2的错误想法呢？因为正排[不是错排]思维导致。把数字2放1位置后的全排列数3！，包含了数字2放1位置且数字1放2位置后的全排列2！导致。

4.总结

本文澄清了错排的递推公式中一个易引起误会的问题，让更多中学生明白错误产生的原因，做题时不再发生此类错误。