Dynamic Analysis of Fractional-Order Memristive Chaotic System
2018-05-07DaweiDingShujiaLiandNianWang
Dawei Ding,Shujia Li and Nian Wang
(School of Electronics and Information Engineering, Anhui University, Hefei 230601, China)
1 Introduction
Memristor, the fourth circuit element, was postulated in 1971 by L.O. Chua[1],which represented a relationship between charge and flux. In memristive system, the nonlinear characteristics of memristor is indispensable. It could bring about the chaos. In 2008, researchers of HP labs fabricated the first memristor[2]. Memristors’ potential applications span multitudinous fields ranging from modeling neural networks[3]to applying nano-scale’s nonvolatile memories[4]. Since memristor is a basic circuit element, the applications of circuit based on memristor are also a research hot spot[5], especially in chaotic circuits, for example, Dasgupta et al.[6]put forward a chaotic circuit based on memristor which was applied in image encryption.
Recently, many physical systems have been found to display fractional-order dynamics, and researches about system with fractional-order have attracted increasing attention. Fractional calculus involves in many fields, for example, in physics[7], electrical circuit theory[8], control systems[9], signal processing[10-11], and chemical mixing[12]. Particularly, it plays a great significant role in chaos theory, which means that chaotic phenomena are existent in fractional order dynamic systems. In 1995, Chua system with fractional-order[13]was firstly presented by Hartley, and he pointed out that when the system’s total order was less than 3, the system would exhibit chaotic behavior. Then Lorenz system with fractional-order was studied by Griagorenko et al.[14], and its chaotic dynamics was also analyzed. In 2010, Petrš provided memristor-based Chua’s circuit[15]with fractional order. It has also other fractional-order counterparts proposed in Refs.[16-18]. Moreover, the chaotic circuit system with fractional order has also achieved great progress. For instance, Shaik et al.[19]realized an experimental circuit system which was a simple modulus nonlinearity jerk equation, and they also used the function of a variable control parameters to study the chaotic behavior. Meanwhile, several systems with fractional-order derived from the corresponding integer-order system have been proposed.
In the paper, a quadratic memristor function is used in the chaotic circuit using the flux-controlled memristor[20]to replace the Chua’s circuit’s diode. Recalling that applications of traditional Chua’s system may be multitudinous, while the analyses of this fractional-order memeristor Chua’s system are few. In particular, to demonstrate the chaotic dynamics, the theoretical analysis of its dynamics is described in detail. Meanwhile we study this fractional-order system’s complex chaotic behavior by bifurcation diagrams with different bifurcation parameters and the largest Lyapunov exponent diagram. Fraction-order system can generate complex chaotic behavior with lower order than the integer-order system.
The structure of this paper is as follows. In the second section, we first discuss the mathematical preliminaries of fractional derivative and memristor. The dynamic equations of the fractional-order memristive system are given in the third section. Then in the fourth section, we analyze the stability of equilibrium point about the memristive system with fractional-order. In addition, we discuss phase portraits, bifurcation diagram and largest Lyapunov exponent diagram under different orderqabout the system in Section 5. This paper concludes with a summary of this work in Section 6.
2 Background
2.1 Fractional Calculus
When it comes to fractional calculus, there are many ways to define derivatives presented in Refs.[21-22]. In this paper, we use Caputo[23]to define the fractional derivative:

(1)
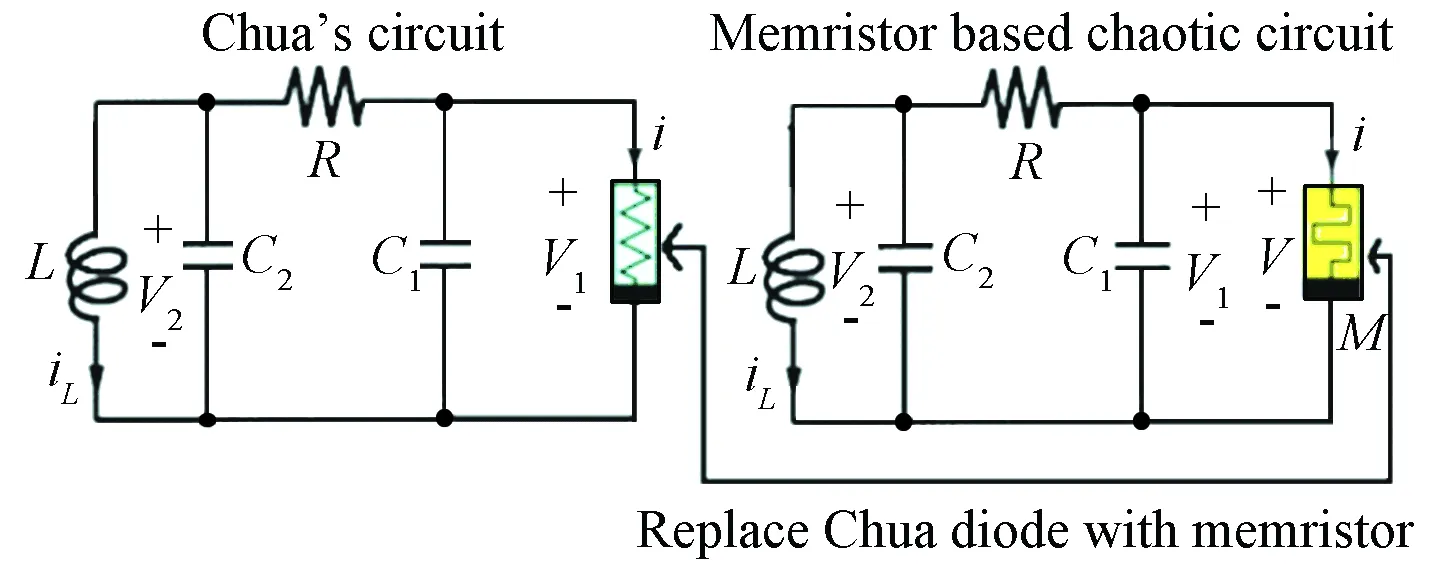
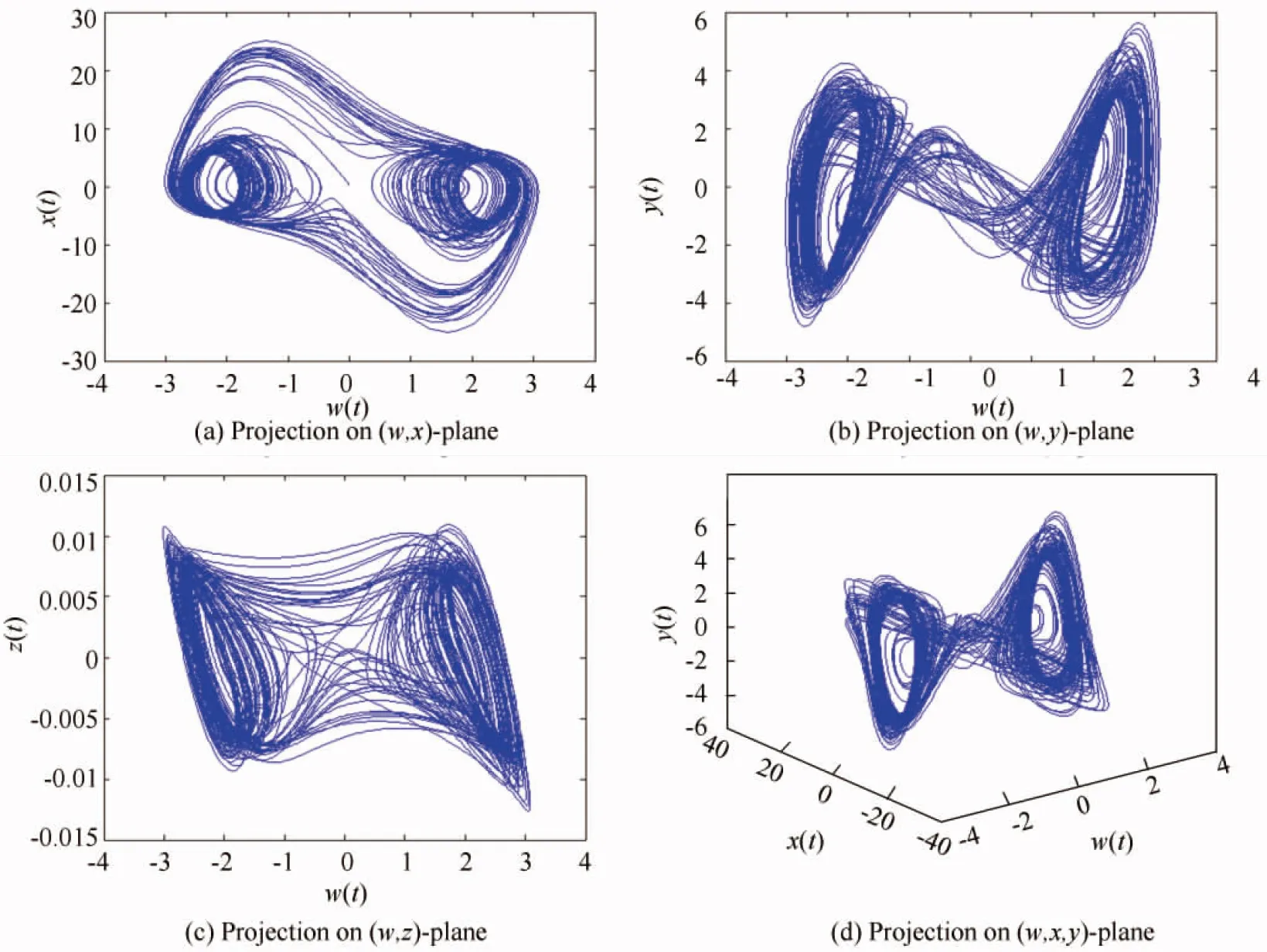
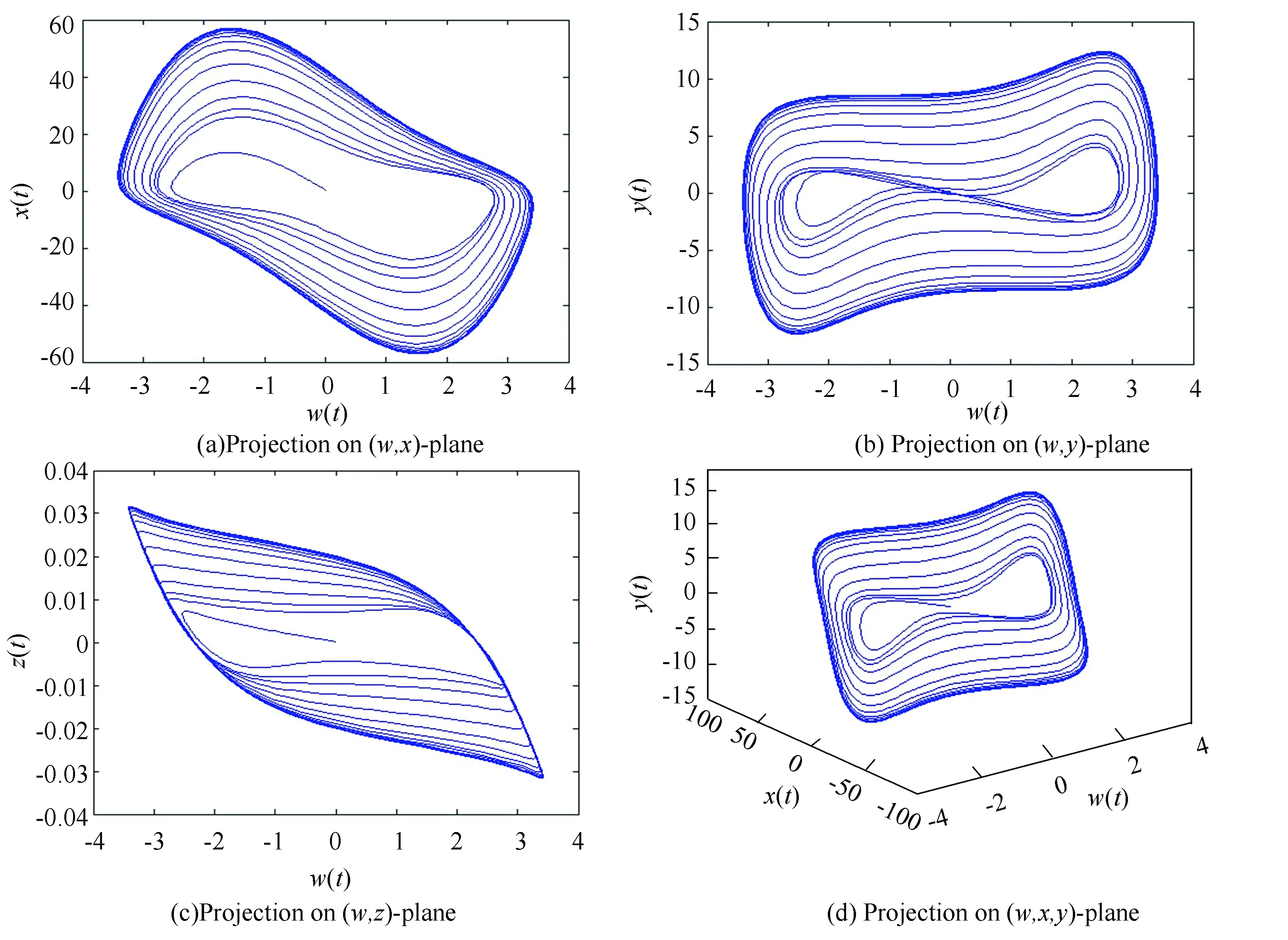
whereΓ(q) is the gamma function,m-1 Memristor is a two-terminal element, which is expressed as a function, and the function describes the relationship between the flux (φ) around the terminals and the charge (Q) that passes through the element. We use a flux controlled memristor in this paper, and express it by a function of its incremental memductanceW(φ): (2) The relationship between the voltagev(t) and currenti(t) through the memristor can be written as: (3) Fig.1 Memristor’s circuit model The integer-order memristive circuit described in this paper is an autonomous Chua’s circuit system presented in Ref.[20], and it simply uses a flux-controlled memristor[25]instead of Chua’s diode. In Fig.2, four fundamental circuit elements including resistorR, capacitorC, inductorL, and memristorM, constitute the memristive dynamical circuit. By utilizing KVL around the loop, the dynamics of the circuit based on memristor[25]are described as: (4) Fig.2 The memristor chaotic circuit Andi(t)is defined by: (5) A cubic nonlinear function was chosen to define theQ(φ) : Q(φ)=αφ+βφ3 (6) It is clear that the model of memristor with smooth nonlinearities would be more easy to be fabricated. And chaos can be occurred in chua’s circuit based on a cubic nonlinear memristor[26]. Thus, the function of memductanceW(φ)is described as: (7) Letα=-0.769×10-3andβ=0.029×10-3in Eq.(6), which is similar to value in Ref.[27]. From the results in Ref.[20], one can point out that, according to simulations in Fig.3, the system can cause chaotic behavior. Fig.3 Lyapunov exponents program of integer-order Chua’s system The fractional equations[28]can be easily deduced from the corresponding integer-order system (4) by making the change as: w≜φ,x≜v1(t),y≜v2(t),z≜iL(t) Then: (8) The initial timet0=0 and orderq∈[0,-1]. Current and voltage variables are rescaled as: By simplifying the equations, we get: (9) DqX=f(X) (10) By solving the following equation, we can calculate the equilibrium point of the system (10) as: Dqx=0⟺f(xeq)=0 Dqx=Jx,(0 (11) where is the Jacobian matrix at the equilibrium point. Now, the following theorem is proposed to explain the stability of linear fractional system (11). Those theorems are stated and proved in Refs.[29-31]. Theorem1[28]If all the eigenvaluesλof the fractional-order system (11)’s Jacobian matrixJsatisfy: The linear system (11) is asymptotically stable. Then, according to the extension of the Lyapunov’s direct method, the Theorem 2 is given to better describe the relationship between the stability of the linear fractional system (11) and nonlinear fractional system (10). Theorem2[28]If the fractional linear system (11) is asymptotically stable at the equilibrium point, then the corresponding fractional nonlinear system (10) is asymptotically stable. Fig.4 The division of unstable and stable regions in systems with fractional-order According to Ref.[32]: if the fractional system (9) is supposed to remain chaotic, a necessary condition is in the unstable region, there is at least one eigenvalueλ. Based on above-mentioned stability results, fractional-order memristive system (9) has a unique equilibrium pointxeq=0 which is readily shown, and have four eigenvalues: Here the eigenvaluesλ2in the unstable region. In Fig.5, it shows the distribution of Jacobian matrixJ’s eigenvalue. Fig.5 Eigenvalue distribution of the fractional-order memristive system The parameters of system (9) are set as those in Ref.[20]:ζ=8 200 Ω·47×10-9nF,L=18 mH,C2=68 nF,C2=6.8 nF. In order to obtain the chaotic attractor,Ris set as 2 000 Ω. We perform the simulation and select the initial conditions as: [w(0),x(0),y(0),z(0)]=[0,0.11,0.11,0] Fig.6 and Fig.7 show the time domain curve and phase plots of a chaotic attractor found withq=0.97. Fig.6 Time-domain plot of the system(9) when q=0.97 Since any system containing at least one positive Lyapunov exponent is defined to be chaotic, we considered the Largest Lyapunov Exponent (LLE)λmaxat first. Then the important problem is how to measure the LLE. The more popular algorithm for calculating LLE is Wolf and Jacobian algorithms[33]. However, for calculating LLE of a fractional order system, Jacobian algorithm is not applicable. Therefore, in this paper, Wolf algorithm[34]is chosen, and the diagram of LLE is plotted in Fig.8. From the figure, we can see whenq>0.93, the system has positive Lyapunov exponents. Namely, the system generates chaos whenq>0.93, which is consistent with the result in bifurcation diagram shown in Fig.9. We simulate the system withR=2 000, and 0.8≤q≤1, the increment ofqis 0.000 5. Bifurcation diagram with bifurcation parameterqis shown in Fig.9. From the bifurcation diagram , we can see when 0.8 Fig.7 Chaotic attractor for system (9) when q=0.97 Fig.8 LLE versus q from 0.8 to 1 step with 0.02 Fig.9 Bifurcation diagram with parameter q increasing from 0.8 to 1 Fig.10 Limit-cycle of the system (9) when q=0.8 Fig.11 Phase portraits of system (9) when q=92 Now, when we chooseq=0.97, the system can be calculated numerically withR∈[1 000,2 400]. From the bifurcation diagram with bifurcation parameterRin Fig.12, we can see whenR<1 800 andR>2 100 the system is in a relatively steady state, whenRis in the range of [1 800,2 100], the system exhibits nonlinear or chaotic-like behavior. In order to demonstrate the chaotic-like behavior, we calculate the Lyapunov exponents with different value ofR, and the results are listed in Table 1. Considering numerical error in the calculation process, we analyze Lyapunov exponent which is less than 0.01 to be equivalent to zero. WhenRis set as 1 500 Ω and 2 300 Ω, the system remains stable and trajectories converge as shown in Fig.13. Fig.12 Bifurcation diagram vs. R Table 1 Lyapunov exponents Fig.13 Phase plane projection of system (9) when R=1 500 and R=2 300 Ω In this article, dynamic behaviors of memristive system with fractional-order are studied via stability analysis and numerical simulations. The phase diagrams, bifurcation diagrams and LLE show that the fractional-order memristive system exhibits chaos when the system parameters exceed the certain threshold. LLE is calculated by the Wolf algorithm, which was readily used in preview research. The simulation results show the effectiveness of the algorithm, and good agreement with theoretical analysis. [1]Chua L O. Memristor-The missing circuit element. IEEE Transactions on Circuit Theory, 1971, 18(5):507-519. [2]Strukov D B, Snider G S, Stewart D R, et al. The missing memristor found. Nature, 2008, 453(7191): 80-83. DOI:10.1038/nature06932. [3]Cai Z, Huang L, Zhang L. New conditions on synchronization of memristor-based neural networks via differential inclusions. Neurocomputing, 2016, 186(23):235-250. DOI:10.1016/j.neucom.2015.12.084. [4]Vourkas I, Sirakoulis G C. Memristor-Based Nanoelectronic Computing Circuits and Architectures. Berlin: Springer International Publishing, 2016.1-28. [5]Yesil A, Babacan Y, Kacar F. A new DDCC based memristor emulator circuit and its applications. Microelectronics Journal, 2014, 45(3):282-287. DOI:10.1016/j.mejo.2014.01.011. [6]Dasgupta T, Paral P, Bhattacharya S,et al. Grayscale image encryption based on high-dimensional fractional order Chua’s system. Advanced Computing, Networking and Informatics, 2014, 2(2): 317-324. DOI:10.1007/978-3-319-07350-7_35. [7]Tarasov V E. Review of some promising fractional physical models. International Journal of Modern Physics B, 2013, 27(9):187-205. DOI:10.1142/S0217979213300053. [8]Shen W, Zeng Z, Zou F. Intelligent Computing Theory. Berlin: Springer International Publishing, 2014. 838-844. [9]Liu X, Xu Y. Bogolyubov-type theorem with constraints generated by a fractional control system. Fractional Calculus & Applied Analysis, 2016, 19(1):94-115. DOI:10.1515/fca-2016-0006. [10]Aslam M S, Raja M A Z. A new adaptive strategy to improve online secondary path modeling in active noise control systems using fractional signal processing approach. Signal Processing, 2014, 107(C):433-443. DOI:10.1016/j.sigpro.2014.04.012. [11]Gonzalez E A, Petras I. Advances in fractional calculus: Control and signal processing applications. Proceedings of the 2015 Carpathian Control Conference (ICCC), 2015 16th International. Szilvasvarad, 2015.147-152. DOI:10.1109/CarpathianCC.2015.7145064. [12]Oldham K B, Spanier J. The Fractional Calculus. New York: Academic Press, 1974. 1947-1953. [13]Hartley T T, Lorenzo C F, Qammer H K. Chaos in a fractional order Chua’s system. IEEE Transactions on Circuits & Systems I:Fundamental Theory & Applications, 1995, 42(8):485-490. [14]Grigorenko I, Grigorenko E. Chaotic dynamics of the fractional lorenz system. Physical Review Letters, 2003, 91(3):034101-034101. DOI:10.1103/PhysRevLett.91.034101. [15]Petráš I. Fractional-order memristor-based Chua’s circuit. IEEE Transactions on Circuits and Systems II: Express Briefs, 2010, 57(12): 975-979. [16]Petráš I. Chaos in fractional-order population model. International Journal of Bifurcation & Chaos, 2012, 22(4):1250072. DOI:10.1142/S0218127412500721. [17]Bai J, Wen G, Rahmani A, et al. Consensus with a reference state for fractional-order multi-agent systems. International Journal of Systems Science, 2015, 47(1):222-234. DOI:10.1080/00207721.2015.1056273. [18]Elsadany A A, Matouk A E. Dynamical behaviors of fractional-order Lotka-Volterra predator-prey model and its discretization. Journal of Applied Mathematics & Computing, 2015, 49(1):269-283. DOI:10.1007/s12190-014-0838-6. [19]Shaik K B, Mandal M K. Chaos from jerk circuit. Resonance, 2010, 15(3):257-267. DOI:10.1007/s12045-010-0039-z. [20]Muthuswamy B. Implementing memristor based chaotic circuits. International Journal of Bifurcation & Chaos, 2012, 20(5):1335-1350. DOI:10.1142/S0218127410026514. [21]Wang M L, Chang R Y, Yang S. Generalization of generalized orthogonal polynomial operational matrices for fractional and operational calculus. International Journal of Systems Science, 1987, 18(5):931-943. DOI: 10.1080/00207728708964020. [22]Gorenflo R, Mainardi F. Fractional calculus: Integral and differential equations of fractional order. Mathematics, 2008, 49(2):277-290. [23]Michele C. Linear models of dissipation whose Q is almost frequency independent-II. Geophysical Journal International, 1967, 13(5):529-539. DOI:10.1111/j.1365-246X.1967.tb02303.x. [24]Davison M, Essex C. Fractional differential equations and initial value problems. Math Scientist, 1998, 23(2):108-116. [25]Muthuswamy B, Kokate P P. Memristor-Based Chaotic Circuits. IETE Technical Review, 2009, 26(6):417-429. DOI:10.4103/0256-4602.57827. [26]Zhong G Q. Implementation of Chua’s circuit with a cubic nonlinearity. IEEE Transactions on Circuits & Systems I Fundamental Theory & Applications, 1995, 41(12):934-941. DOI:10.1109/81.340866. [27]Khalil K H. Nonlinear Systems.3nd ed. New Jersey: Prentice Hall,2002. [28]Donato C, Giuseppe G. A novel memristor-based chaotic system with fractional order. Proceedings of the 2014 International Conference on Fractional Differentiation and ITS Applications. Piscataway:IEEE, 2014.1-6. DOI: 10.1109/ICFDA.2014.6967415. [29]Cafagna D, Grassi G. On the simplest fractional-order memristor-based chaotic system. Nonlinear Dynamics, 2012, 70(2):1185-1197. DOI:10.1007/s11071-012-0522-z. [30]Teng L, Lu Herbert H C, Wang X Y, et al. Chaotic behavior in fractional-order memristor-based simplest chaotic circuit using fourth degree polynomial. Nonlinear Dynamics, 2014, 77(1/2):231-241. DOI:10.1007/s11071-014-1286-4. [31]Delavari H, Baleanu D, Sadati J. Stability analysis of Caputo fractional-order nonlinear systems revisited. Nonlinear Dynamics, 2012, 67(4):2433-2439. DOI:10.1007/s11071-011-0157-5. [32]Tavazoei M S, Haeri M. A necessary condition for double scroll attractor existence in fractional-order systems. Physics Letters A, 2007, 367(1/2):102-113. DOI:10.1016/j.physleta.2007.05.081. [33]Meng J, Zhu T Y, Chen X, et al. The nonlinear dynamics characteristics of stock market and its variation. Applied Mechanics & Materials, 2014, 513-517:3188-3193. DOI:10.4028/www.scientific.net/AMM.513-517.3188. [34]Wolf A, Swift J B, Swinney H L, et al. Determining Lyapunov exponents from a time series. Physica D Nonlinear Phenomena, 1985, 16(3):285-317. DOI:10.1016/0167-2789(85)90011-9.2.2 Memristor Model

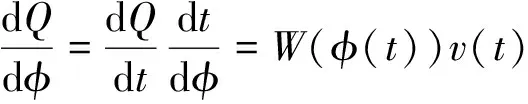
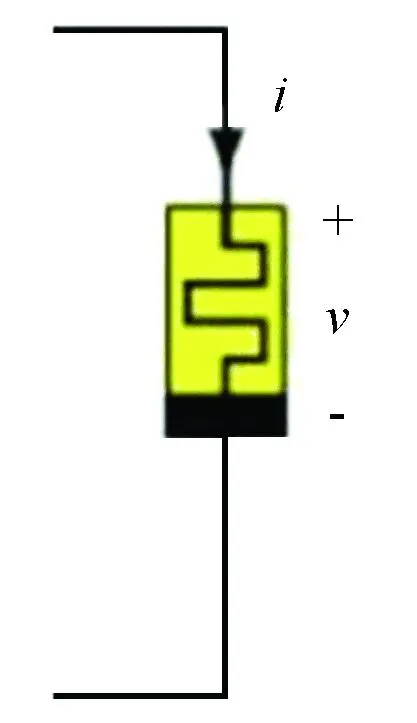
3 Memristive Chaotic System Based on Chua’s Circuit
3.1 Integer-Order Case
3.2 Fractional-Order Case


4 Stability Analysis of Memristive Chaotic System with Fractional-Order


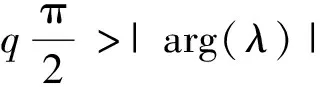



5 Numerical Simulations






6 Conclusions
杂志排行
Journal of Harbin Institute of Technology(New Series)的其它文章
- Review:Application of the CALPHAD Approach and First-Principles Calculations to Electrode Materials in Li Ion Batteries
- Improved Ship Target Detection Accuracy in SAR Image Based on Modified CFAR Algorithm
- An Optimization Method for a Single Machine Multi-family Scheduling Problem with Qualification Run Constraints
- Modeling of Geometric Variations Within Three-Dimensional Tolerance Zones
- Comprehensive Assessment of Pilot Mental Workload in Various Levels
- Design and Testing of a Novel Passive Isolator for a Space Optical Payload
