中国工业水资源利用效率的空间收敛效应
2018-05-07宋晓娜薛惠锋王海宁
张 峰,宋晓娜,薛惠锋,王海宁
(1.山东理工大学 管理学院,山东 淄博 255012;2.中国航天系统科学与工程研究院,北京 100048;3.泰山学院 商学院,山东 泰安 271000)
随着全球经济的高速发展与工业化水平的提升,对于资源的需求程度愈加突出,水资源作为一种基础性的自然资源,在整个生态环境中发挥着重要的作用,是自然环境的关键组成要素之一,同时,水资源作为一种战略性的经济资源,在整个国民经济和社会发展中也具有举足轻重的支撑作用。尤其是在当前工业发展处于转型关键期的背景下,提高工业水资源利用效率已成为实现新型化发展的重要途径,也是缓解全国水资源供需矛盾的关键环节。然而,在区域经济发展与资源利用关联度愈加紧密的情况下,一些区域水资源管理政策通常会对其他相关区域发展造成多方面影响。这就要求相关部门在制定工业发展及水资源开发利用政策措施时,按照“宏观分析—区域把控—行业调整”的整体思路,提高对中国工业水资源利用效率进行科学的宏观分析、区域工业水资源配置的精准判断以及工业行业水资源利用的决策优化水平。
一、文献回顾
近年来,学者们对工业水资源利用与保护的研究不断深入,以期能够进一步挖掘工业水资源可持续发展潜力。埃诺瑞等(Alnouri et al.,2015)认为当前工业用水普遍存在耗水量大、外排污染严重、水处理成本较高等系列问题,这难以支撑工业长期发展的需求[1]。尤森等(Yousen et al.,2015)以工业系统中水资源利用与减排成本作为主要考察指标,通过计算化学需氧量(COD)和氨氮(NH4-N)的可减少量,认为中国工业系统中水资源利用与减排仍具有较大的提升空间,尤其是在各地区工业水资源利用效率差异化显著的情况下,强化政策导向作用与水资源储备战略成为关键[2]。沃尔什等(Walsh et al.,2016)认为提高工业水资源开发利用的管理水平是企业履行其社会责任重要过程,而在实际的企业运营过程中,水资源利用的成本控制易被忽略,需要进一步完善水资源价值评估体系及其仿真系统,并将信息通信技术引入其整个过程当中,以此缓解工业发展中的水资源不足、浪费严重等问题[3]。
国内诸多学者在工业水资源利用效率、污染控制、影响机制等问题上也展开了多方面的探讨。如沈满洪等(2015)通过评估中国28个省级区域工业水资源利用效率及污染排放状况,发现在全国工业水资源利用效率总体上呈稳步上升的态势下,局部地区仍出现了工业全要素生产效率下降的现象[4]。买亚宗等(2014)分别建立了工业用水效率与环境效率测度模型,研究发现各区域经济产出水平虽然较高,但同时对水环境产生的不良影响却异常严峻,特别是西部地区工业用水污染问题严重,而南方地区表现出较高的工业节水潜力[5]。陈东景(2008)认为工业水资源消耗强度总体呈下降趋势,这是其结构份额与效率份额共同演化的结果,两种份额变动呈相反态势,其中前者下降而后者为稳步上升,电力热力的生产供应业的结构份额最大[6]。孟戈等(2013)认为建立工业用水效率控制的“红线考核指标体系”是加快推进最严格水资源管理制度落实的关键内容之一,该体系将节水管理、节水投入、节水技术等指标纳入考虑范畴[7]。此外,王树鹏等(2011)、刘晓等(2014)分别针对云南省、北京市水资源管理及用水效率评价指标体系进行了探索性构建,用于支持不同区域用水状态的评价[8-9]。
综上,提高工业水资源利用效率不仅是缓解当前水资源危机的重要途径,也是支撑工业可持续发展的关键,而限于国内各省级区域工业化水平与水资源禀赋等因素的影响,不同时期省级区域之间的工业水资源利用效率必然存在一定的差异性。而时序视角下中国各省级区域工业水资源利用效率究竟变动态势如何?各省级区域之间的效率差异是在逐步缩小还是扩大?在地理空间作用下各省级区域工业水资源利用效率又会受到怎样的影响?解决上述问题对于提高工业水资源利用相关政策制定与实施过程的科学水平,推动区域经济均衡化发展至关重要。鉴于此,本文尝试在测度工业水资源利用效率的基础上,选取空间收敛模型辨识1997—2014年中国各省级区域工业水资源利用效率的收敛态势,为动态评估中国工业水资源利用水平提供理论参考。
二、模型构建
(一)工业水资源利用效率σ收敛
工业水资源利用效率σ收敛侧重于分析各个区域工业水资源利用效率发展水平的差距,指的是各区域工业水资源利用效率发展水平的差距随时间而逐步缩小,最终工业水资源利用效率较低的区域追赶上工业水资源利用效率水平较高的地区。区域工业水资源利用效率的σ收敛一般用标准差指标表示:
(1)

(二)工业水资源利用效率β收敛
工业水资源利用效率β收敛的含义是指工业水资源利用效率水平较低的区域其工业水资源利用效率水平增长速率通常要高于工业水资源利用效率水平较高区域,即各区域的工业水资源利用效率增长速度与工业水资源利用效率水平之间存在负相关关系[10]。β收敛可被进一步划分为绝对β收敛与条件β收敛。
1.工业水资源利用效率绝对β收敛
区域工业水资源利用效率绝对β收敛可以表示为:
(2)

(3)
2.工业水资源利用效率条件β收敛
区域工业水资源利用效率条件β收敛考虑了不同区域的经济水平、产业结构、技术层次、环境政策等方面存在的差异,它意味着不同区域的工业水资源利用效率将收敛于各自的稳定水平[11]。在区域工业水资源利用效率绝对β收敛模型的基础上,通过引入相应控制变量,可将其绝对β收敛转化为条件β收敛。区域工业水资源利用效率条件β收敛模型可表述为:
(4)
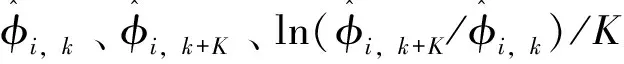
(5)
三、变量选取与数据说明
本文利用张峰等(2017)的非强制性幅度调整RAM-SFA-RAM三阶段组合效率测度模型,补充其研究中的中国30个省级区域(西藏、澳门、台湾和香港除外)1997—2014年工业水资源利用效率[12]。而对于工业水资源利用效率条件β收敛测度模型中控制变量Xl,i,k的选取则主要基于影响其水资源利用效率环境要素视角。据此,本文在吸收现有研究经验的基础上[13-15],分别将区域自然禀赋、经济水平、产业结构、高技术导向水平、用水结构和社会水平作为其环境影响要素,分别选用区域水资源总量X_twr(m3)、人均GDPX_ecl(万元)、第二产业比重X_sps、高技术产业R&D经费与主营业务收入比重X_crq、水资源消耗总量与水资源总量比重X_tsc、人均教育经费X_pel(千元)作为代表性指标,各指标描述性统计情况见表1。
本文样本数据源于《中国统计年鉴》(1998—2014年)、《水资源公报》(1997—2014年)、《中国工业经济统计年鉴》(1998—2014年)、《中国环境统计年鉴》(1998—2014年)和各地市统计年鉴等,少数地区的时序缺水数据采用邻近年限中值或拟合值补充。

表1 自变量及其描述性统计
四、空间收敛效应实证检验
(一)工业水资源利用效率空间关联检验
为避免工业水资源利用效率出现“伪收敛”检验,需对其效率空间分布状态进行检验。全局莫兰指数是可用于判断要素的属性分布是否有统计上显著的聚集或分散现象的常用方法,按照孙等人(Sun et al.,2013)的做法,本文测度了工业水资源利用效率的全局莫兰指数值[16]。可知样本省级区域工业水资源利用效率具有显著正向空间集聚,即表明各省级区域工业水资源利用效率于空间维度存在相对显著的正向自相关特征,其状态属性为具有较高工业水资源利用效率的省级区域与具有相关较高效率的省级区域趋近,而相对较低效率的省级区域则趋近于较低效率的省级区域。同时,全局莫兰指数在时序维度上虽然存在局部年份的短期波动,但在整体上表现为持续上涨态势,说明各省市工业水资源利用效率集聚水平尽管存在强弱交替现象,但总体水平不断增强。这印证了对于工业水资源利用效率的研究中地理空间因素所产生的影响不可被轻易忽略,尤其是选取空间计量模型对其空间效应检验时,需考虑工业水资源利用效率的空间收敛性。
(二)工业水资源利用效率σ收敛测度及结果分析
在构建工业水资源利用效率空间收敛分析模型的基础上,本文选取全国、东部、中部和西部地区工业水资源利用效率作为测度对象,利用测度的工业水资源利用效率1997—2014年面板数值,按照工业水资源利用效率σ收敛测度模型对各区域工业水资源利用效率的标准差及其变动趋势进行评估,见表2。

表2 区域工业水资源利用效率σ收敛测度结果
根据表2可知,工业水资源利用效率的σ收敛于宏观层面呈现为“整体发散,局部收敛”的基本演变特征。而具体到全国来看,工业水资源利用效率指数标准差于1997—2014年表现为逐步提高的发展态势,即由1997年的效率指数标准差0.437 1提高至2014年的1.940 1,尤其是在2002—2004年、2007—2008年和2010—2014年,其标准差值呈现出较大的变动幅度。该结果说明在测度样本区间内,中国区域间工业水资源利用效率的绝对差异表现为逐步扩大的趋势。所以,可认为1997—2014年全国层面的区域工业水资源利用效率不具有σ收敛的变动态势。
东部、中部和西部地区的工业水资源利用效率指数标准差在1997—2014年呈现出了差异化的变动特点。其中,东部地区工业水资源利用效率指数的标准差虽然与全国层面存在波动幅度的差异性,但其在1997—2008年表现出与全国指数标准差相似的变化趋势,即趋于平缓的“N”型σ发散曲线,其发散趋势于2009—2010年仍然持续,到2011—2013年标准差的差值趋于稳定,即呈现出σ收敛,但其标准差于2014年又趋于相对较大幅度增加,可见东部地区工业水资源利用效率绝对差异处于调整波动状态。中部地区除了在2004—2006年表现出一定的σ收敛趋势外,剩余样本区间内工业水资源利用效率指数标准差始终处于逐步提升的状态下,到2014年,已由最初1997年的0.203 7提升至2014年的0.822 1,呈现出σ“发散—收敛—发散”的变动趋势。西部地区工业水资源利用效率指数标准差尽管相比全国、东部和中部地区整体变动幅度相对较弱,但其在样本时段内长期处于σ发散状态,尤其是于2005—2008年其变动也呈现出了“N”型σ发散曲线,且波动幅度相对较大。
此外,同比东部、中部和西部地区工业水资源利用效率指数标准差,可以发现东部地区其效率指数标准差要明显大于中部和西部地区,说明东部地区工业水资源利用效率区域差异性相对显著。而中部地区次之,西部地区工业水资源利用效率区域差异最弱,但从近3年的标准差变动幅度来看,西部地区的效率指数标准差具有追赶中部地区的态势,如2012年中、西部地区其效率指数标准差的差值为0.180 6,到2013年时缩减到0.176 5,而到2014年该差异进一步削弱,差值降低为0.149 4,说明相比中部地区,西部地区工业水资源利用效率的区域差异性正在逐步提升。
(三)工业水资源利用效率绝对β收敛测度及结果分析
为进一步辨析中国区域工业水资源利用效率增长速率与其效率水平之间的动态关系,本文利用工业水资源利用效率绝对β收敛模型分别检验中国全国、东部、中部和西部层面的区域工业水资源利用效率指数的绝对β收敛性,结果见表3。从中可发现,全国、中部和西部地区的工业水资源利用效率指数绝对β收敛模型分别通过了1%、5%和1%显著性水平下的LR检验,据此可对其选择固定效应模型。而东部地区工业水资源利用效率指数β收敛模型的LR与豪斯曼检验均呈现出非显著性,对此在考虑各效应检验模型的拟合优度及杜宾检验值的基础上,选取混合效应模型对其进行估计。为避免截面数据异方差对测度结果的影响,此处选取period SUR方法对上述各模型进行回归测度[17]。按照测度结果,可认为除了中部地区效应模型是通过了5%显著水平的F检验外,其余全国、东部和西部地区的效应模型均是以1%的显著水平通过其检验,而杜宾检验值在[1.8,2.4]区间内,该结果说明上述效应模型的选取满足测度要求,可对区域期初工业水资源利用效率与其增长速率之间的关系进行客观描述。

表3 区域工业水资源利用效率绝对β收敛测度结果
注:变量系数为历史年份下的系数均值;***、**、*分别表示1%、5%和10%显著水平;括号内为t值。
据表3可知,全国层面期初工业水资源利用效率指数系数估计值为-0.131 6,并达到1%显著性水平检验的要求,表明期初全国工业水资源利用效率指数与其增长率成负向相关关系,即说明从全国整体水平来看,工业水资源利用效率指数存有β收敛态势,测度省市工业水资源利用效率呈现趋同收敛的特点。而在东部、中部和西部地区的β收敛测度中,东部和中部地区工业水资源利用效率指数系数估计与全国层面测度相似,均为负值(分别为-0.108 9、-0.162 6),于1%的显著性水平表现为β收敛趋势。此结果说明东、中部地区内各区域工业水资源利用效率差异正在逐步缩小,这与现实情况相符合,东部地区工业经济发展水平较高,其水资源开发与节水设备、技术相对先进,地域之间经济差异相对较小,而在东部地区工业带动及自身发展的作用下,中部地区工业水资源利用还未出现显著性的规模差异。相比东部和中部,西部地区测度的期初工业水资源利用效率指数系数显著并为正值(0.091 1),说明该地区期初工业水资源利用效率指数与其增长速率具有正向相关关系,其工业水资源利用效率指数暂且不具有绝对β收敛,无趋同收敛的特点,即工业水资源利用效率较高区域的工业水资源利用效率攀升速率也愈加显著,而此状态下易引发区域之间工业水资源利用效率的差异逐步变大,表现出相对发散的演变态势。
(四)工业水资源利用效率条件β收敛测度及结果分析
1.单控制变量测度下的工业水资源利用效率条件β收敛。利用全国层面的单控制变量历史数据代入工业水资源利用效率指数条件β收敛模型,取得全国层面的收敛性测度结果,见表4。其中,δ系数值为研究样本中各省市的参数测度平均值,而要素X_tsc和X_pel进行豪斯曼检验和LR检验时呈现非显著性,则此处选取混合效应模型对其进行检验。由此可知,各估计方程期初工业水资源利用效率指数水平的系数测度值μ均显著性小于0,表明若仅考虑单一控制变量时,这些要素可对全国层面工业水资源利用效率指数的条件β收敛起到推动作用。而根据上述影响要素的υ系数值,可知除人均教育经费X_pel未通过显著性检验以外,其余指标均在1%显著水平下通过了其检验,各变量的系数υ值均为正也说明该类要素对中国工业水资源利用效率条件β收敛起到显著推进作用,而人均教育经费X_pel对中国工业水资源利用效率条件β收敛的作用强度并不显著。

表4 全国层面工业水资源利用效率单变量回归检验结果
注:变量系数为历史年份下的系数均值;***、**、*分别表示1%、5%和10%显著水平;括号内为t值。
据表5中对于东部地区的工业水资源利用效率指数条件β收敛测度结果(按照豪斯曼检验和LR检验的显著性,除了要素X_tsc使用混合效应检验外,其余均采取固定效应检验),可知其各要素的μ系数测度值都小于零,其中,除了要素X_twr通过10%水平的显著性检验,要素X_sps、X_crq通过5%水平的显著性检验外,其余要素均以1%水平通过了显著性检验,表明若仅考虑上述单一控制要素时,该地区工业水资源利用效率存有条件β收敛的趋势。同时,根据控制要素υ系数值测度情况,可发现要素X_ecl、X_crq和X_pel均通过了1%显著性检验,而X_tsc则通过5%显著性检验,说明该区域经济水平、高技术导向水平、用水结构和社会水平可对东部地区工业水资源利用效率的条件β收敛可起到促进作用。而要素X_twr和X_sps则未能通过其相应水平的显著性检验,即说明该系列要素对促进东部地区工业水资源利用效率条件β收敛所发挥的作用并不显著。

表5 东部地区工业水资源利用效率单变量回归检验结果
注:变量系数为历史年份下的系数均值;***、**、*分别表示1%、5%和10%显著水平;括号内为t值。
据中部地区工业水资源利用效率单变量回归检验结果(按照豪斯曼检验和LR检验的显著性,要素X_twr、X_ecl使用混合效应检验,剩余要素均采取固定效应检验,计算步骤同东部地区,限于篇幅,中西部地区检验数值结果未列出),可发现各要素为单控制变量时,其回归检验方程的系数μ值均小于零,其中,要素X_twr、X_ecl、X_sps和X_crq的μ系数通过了1%显著性水平检验,而要素X_pel处于5%显著性水平,要素X_tsc未能够通过各相应显著性水平的检验。该结果说明在单变量回归检验的条件下,中部地区工业水资源利用效率具有条件β收敛趋势,但若仅将用水结构作为其控制变量时,则中部地区工业水资源利用效率不具有显著的条件β收敛趋势。按照各要素的υ系数值测度情况,可知要素X_twr未能通过各相应水平的显著性检验,即相比之下,自然禀赋对中部地区工业水资源利用效率的条件β收敛不具备显著影响。区域经济水平、产业结构、高技术导向水平、用水结构、社会水平均通过了1%显著性水平的检验,说明上述各要素对中部地区工业水资源利用效率的条件β收敛发挥显著促进作用。
由西部地区工业水资源利用效率的单变量回归检验结果可知,在各要素检验均使用固定效应检验的前提下,各回归方程的要素系数μ均小于零,同时除了要素X_crq是通过5%显著性水平检验以外,其余要素均通过了1%显著性水平检验,表明在控制于单要素变量的情况下,西部地区工业水资源利用效率具有呈条件β收敛的态势。但从测度的υ系数值,发现仅有要素X_sps、X_tsc通过了1%显著性水平检验,而X_ecl则通过了10%显著性水平检验,其余要素均未符合相应显著性水平检验的要求,即说明当前环境下区域自然禀赋、经济水平、高技术导向水平和社会水平均无法实现对该地区工业水资源利用效率的条件β收敛显著促进,尤其是西部地区的自然禀赋对西部地区工业水资源利用效率的条件β收敛呈现非显著的负向作用,而产业结构、用水结构对西部地区工业水资源利用效率条件β收敛起到相对显著的促进作用。
2.多控制变量测度下的工业水资源利用效率条件β收敛。基于单控制变量的工业水资源利用效率条件β收敛性分析可在一定程度上反映所选要素对区域工业水资源利用效率的影响水平,但要达到辨识各要素对工业水资源利用效率条件β收敛作用过程中发挥的相互影响,判定多要素复合作用下区域工业水资源利用效率变化的内在机理,还需要进行基于多控制变量的工业水资源利用效率条件β收敛分析。
鉴于单变量回归检验时,要素X_pel在全国层面的工业水资源利用效率测度中呈非显著,因此,对全国层面工业水资源利用效率条件β收敛进行多变量回归检验,剔除要素X_pel,并按照式(5)取得其他样本要素测度结果,见表6。据此可知,各测度要素的回归系数μ均小于零,这进一步印证了全国层面的工业水资源利用效率具有条件β收敛的趋势。其中,模型1测度中的要素X_twr、X_sps和X_crq的回归系数υ′均为正,且满足显著性检验的要求。上述结果与单变量的回归检验结果相一致,表明自然禀赋、产业结构和高技术导向水平是促进全国层面工业水资源利用效率实现条件β收敛的关键驱动要素。而对于要素X_ecl、X_tsc的回归系数υ′呈非显著,表明同比自然禀赋、产业结构和高技术导向水平,经济水平、用水结构在推动全国层面工业水资源利用效率条件β收敛时起到的作用相对薄弱。模型2是建立在模型1对非显著要素进行剔除处理的基础上进行的检验,测度表明要素X_twr和X_crq通过了显著性检验的要求。在进一步剔除非显著要素X_sps后,建立模型3并进行回归检验,取得结果中自然禀赋和高技术导向水平均通过了显著性检验,拟合效果更高,说明自然禀赋、高技术导向水平对于全国层面工业水资源利用效率条件β收敛的促进作用更加明显。
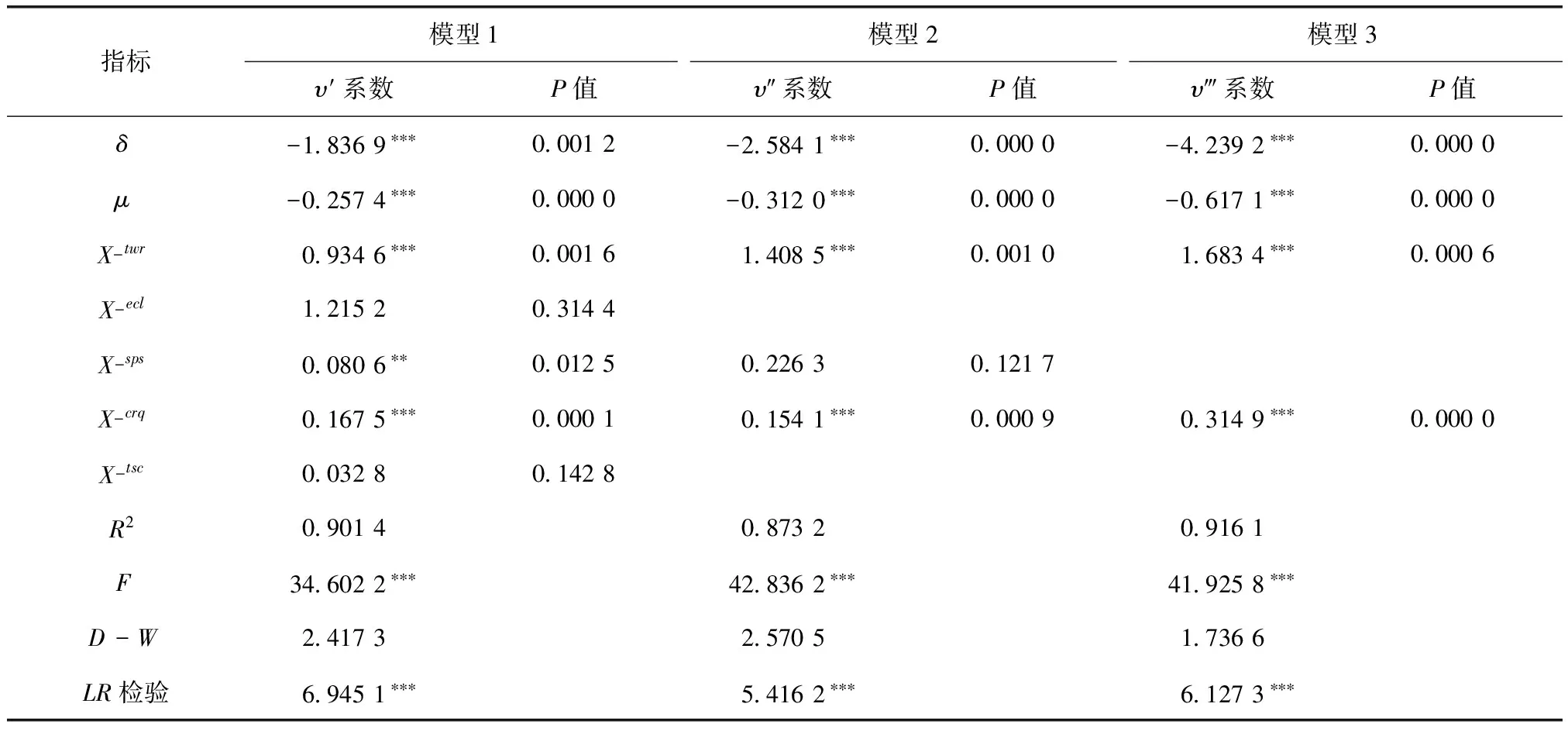
表6 全国层面工业水资源利用效率多变量回归检验结果
注:变量系数为历史年份下的系数均值;***、**、*分别表示1%、5%和10%显著水平;各测度模型均选取固定效应模型。
通过对东部地区工业水资源利用效率进行多变量回归检验分析,取得其效率条件β收敛测度结果,详见表7。其中,可发现各测度模型的要素系数μ都通过了其1%显著性水平检验,且为负值,说明在测度样本区间内,东部地区工业水资源利用效率具有条件β收敛的趋势。
东部地区工业水资源利用效率在进行单变量回归检验分析时,要素X_twr、X_sps均未通过显著性水平检验,因此,在构建多变量回归模型1时,剔除上述要素并进行其他要素的测度检验。据结果可知,要素X_ecl、X_crq、X_pel的υ′系数均为正,并通过了相应水平的显著性检验,说明区域经济水平、高技术导向水平和社会水平三项指标对东部地区的工业水资源利用效率条件β收敛具有相对显著的促进作用。而要素X_tsc的υ′系数虽然为正,但未能通过显著性水平检验,表明同比之下东部地区用水结构对其效率条件β收敛的作用并不显著。在剔除要素X_tsc的基础上,建立回归模型2对要素X_ecl、X_crq和X_pel进行重新检验,结果发现在对上述要素进行统筹分析时,要素X_ecl、X_pel进一步通过了1%的显著性水平检验,而X_crq未能通过显著性检验,说明相比之下,区域经济水平、社会水平对东部地区的工业水资源利用效率条件β收敛发挥的作用更加明显。对此,模型3测度所得的要素X_ecl、X_pel的系数υ′为正,且通过1%显著性水平检验,对上述结论进行了进一步印证。
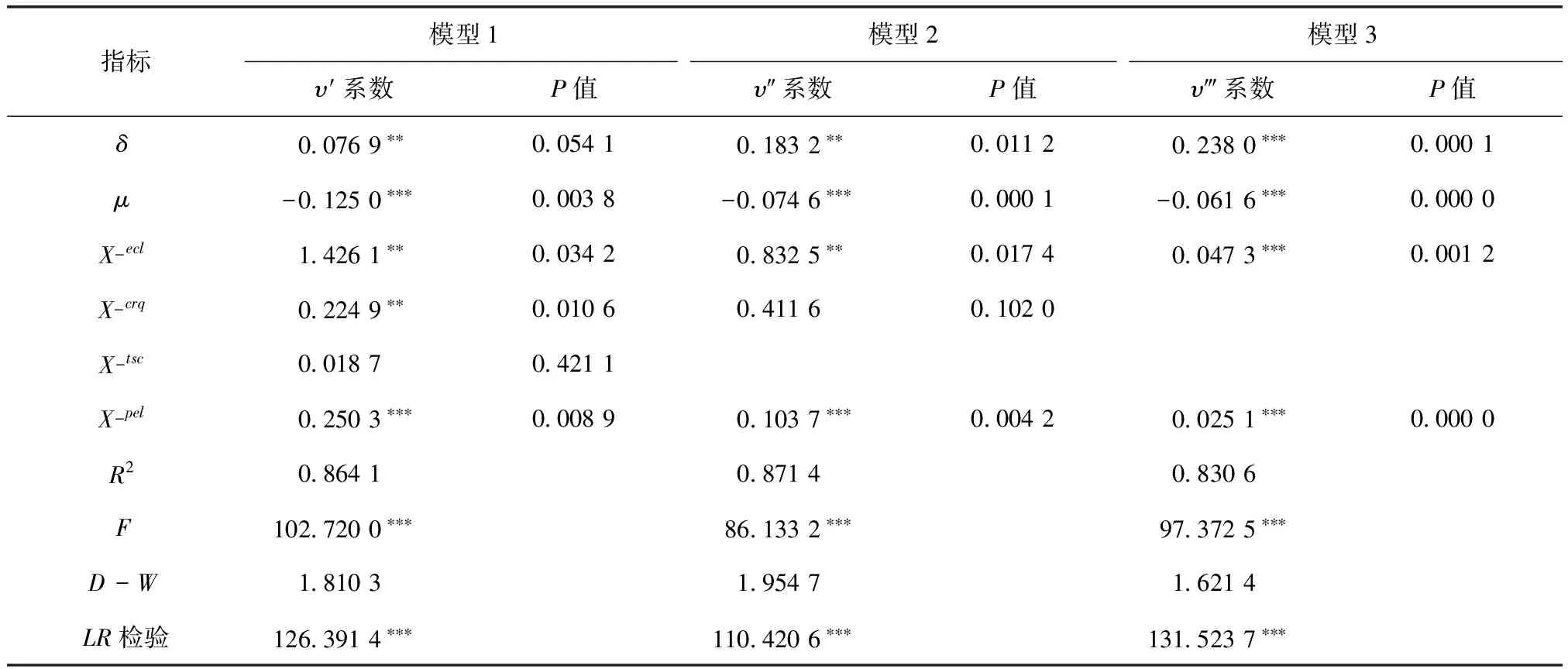
表7 东部地区工业水资源利用效率多变量回归检验结果
注:变量系数为历史年份下的系数均值;***、**、*分别表示1%、5%和10%显著水平;各测度模型均选取固定效应模型。
中部地区的工业水资源利用效率多变量回归检验结果,计算步骤同东部地区,此处限于篇幅,中西部地区具体检验数值结果未列出。根据测度结果,可知各多变量回归模型的要素系数值分别为-0.164 3、-0.142 2和-0.035 7,均为负值且通过了1%显著水平的检验,说明在测度样本区间内,多变量检验的情况下,中部地区工业水资源利用效率同样具备条件β收敛的趋势。
在对中部地区工业水资源利用效率进行单变量回归检验时,仅有要素X_twr未通过相应水平的显著性检验,所以,在对模型1进行回归检验时,将要素X_twr进行了剔除处理。根据测度结果,可知要素X_crq呈现非显著性,即虽然高技术导向水平逐步提升,但相比其他要素,其对于工业水资源利用效率条件β收敛的作用依然偏低。此外,除了要素X_ecl和X_pel分别通过10%与5%显著水平的检验外,其余变量均以1%显著水平通过了检验,说明区域经济水平、第二产业发展、用水结构和社会水平对中部地区工业水资源利用效率条件β收敛可起到相对显著的促进作用。在剔除非显著性要素X_crq后,构建模型2并进行检验,发现该情景下的要素X_ecl呈现出了非显著性,而要素X_sps、X_tsc和X_pel均通过了1%显著水平的检验。进一步对非显著性要素X_ecl进行剔除处理后,所建立的回归模型3测度显示,要素X_sps、X_tsc和X_pel均通过了其显著性检验,且υ‴系数为正,说明同比之下,第二产业发展、用水结构和社会水平对中部地区的工业水资源利用效率条件β收敛的作用性更加明显。
相比全国层面、东部地区和中部地区,西部地区工业水资源利用效率的多变量回归检验模型数量则仅有2个完成了显著性水平检验的要求。其中,根据各要素μ系数的测度结果,可知其要素系数υ′、υ″值均小于零(分别为-0.351 5、-0.269 8),说明在考虑多变量集成测度的情况下,西部地区工业水资源利用效率具有条件β收敛的态势。
按照西部地区工业水资源利用效率单变量回归检验结果,要素X_twr、X_crq和X_pel均未通过显著性检验。据此,在进行西部地区工业水资源利用效率条件β收敛的多变量回归测度时,剔除上述要素,将要素X_ecl、X_sps、X_tsc代入模型,发现除了要素X_ecl的υ′系数呈非显著性外,要素X_sps和X_tsc的υ′系数均通过了1%显著性检验,并为正值。这说明第二产业发展、用水结构对西部地区工业水资源利用效率条件β收敛的促进作用相对明显。在剔除非显著要素X_ecl后,利用模型2取得相应的测度结果,发现剩余要素X_sps、X_tsc的υ″系数均为正(分别为0.750 2、0.448 1),且均通过了1%显著性水平检验。而上述结果进一步印证了要素第二产业发展、用水结构对西部工业水资源利用效率条件β收敛的重要促进作用。
根据上述对中国工业水资源利用效率条件β收敛的单要素与多要素集成测度,可知不同区域工业水资源利用效率虽然具有条件β收敛的趋势,但其主要的驱动要素存在一定差异性。其中,自然禀赋、高技术导向水平是全国层面工业水资源利用效率条件β收敛的关键驱动要素,经济水平、社会水平对东部地区工业水资源利用效率条件β收敛性作用更加明显,第二产业发展、用水结构和社会水平是中部地区工业水资源利用效率条件β收敛的关键驱动要素,而第二产业发展、用水结构则成为促进西部地区工业水资源利用效率条件β收敛的关键驱动要素。综合上述结果,可知各区域在进行工业水资源利用调整的过程中需要全面结合影响要素类别的不同及其作用程度的差异性,既要制定适合本区域发展的政策措施,也需注重区域之间的均衡性动态发展[18]。
五、结论与启示
基于收敛假说理论,分别建立了工业水资源利用效率的σ空间收敛和β空间收敛模型,并利用工业水资源利用效率面板数据对全国、东部、中部和西部地区进行测定。结果发现中国工业水资源利用效率的σ收敛于宏观层面呈现为整体相对发散,而局部存在收敛的基本演变特征,东部地区工业水资源利用效率绝对差异处于调整波动状态,中部地区呈“发散—收敛—发散”的变动趋势,西部地区则长期处于σ发散状态,而通过标准差也可发现相比中部和西部,东部地区工业水资源利用效率区域差异性相对显著;工业水资源利用效率绝对β收敛测度结果表明全国层面、东部和中部地区具有绝对β收敛态势,东、中部地区内各区域工业水资源利用效率差异正在逐步缩小,而西部地区不具有绝对β收敛,表现出相对发散的演变态势。将自然禀赋、经济水平、产业结构、高技术导向水平、用水结构和社会水平作为工业水资源利用效率条件β收敛模型中的影响要素,对其收敛态势进行分别检验。结果表明在单控制变量测度条件下,除了社会水平外,其他要素对全国层面工业水资源利用效率条件β收敛的作用相对显著;经济水平、高技术导向水平、用水结构和社会水平可对东部地区工业水资源利用效率的条件β收敛可起到促进作用;对于中部地区而言,除了上述要素外,产业结构也可促进其工业水资源利用效率条件β收敛;而西部地区中仅有产业结构、用水结构可对其工业水资源利用效率条件β收敛起到相对显著的促进作用。在多控制变量测度条件下,自然禀赋、高技术导向水平是促进全国层面工业水资源利用效率条件β收敛的重要原因;经济水平和社会水平对东部地区工业水资源利用效率条件β收敛发挥作用相对更加明显;而中部地区条件β收敛的原因主要在于产业结构、用水结构和社会水平;产业结构、用水结构则成为促进西部地区工业水资源利用效率条件β收敛的关键驱动要素。因此,各地区工业水资源利用调整的过程中需充分考虑各要素的影响制定符合区域发展的政策措施。
参考文献:
[1]ALNOURI S Y,LINKE P,HALWAGI M E.A synthesis approach for industrial city water reuse networks considering central and distributed treatment systems[J].Journal of Cleaner Production,2015,89:231-250.
[2]Y S WANG.Water use efficiency and related pollutants’ abatement costs of regional industrial systems in China:a slacks-based measure approach[J].Journal of Cleaner Production,2015,101:301-310.
[3]WALSH B P,CUSACK D O,O’Sullivan D.An industrial water management value system framework development[J].Sustainable Production and Consumption,2016,5:82-93.
[4]沈满洪,程永毅.中国工业水资源利用及污染绩效研究——基于2003—2012年地区面板数据[J].中国地质大学学报(社会科学版),2015(1):31-40.
[5]买亚宗,孙福丽,石磊,等.基于DEA的中国工业水资源利用效率评价研究[J].干旱区资源与环境,2014(11):42-47.
[6]陈东景.中国工业水资源消耗强度变化的结构份额和效率份额研究[J].中国人口·资源与环境,2008(3):211-214.
[7]孟戈,邱元锋,沈珍.工业用水效率控制红线考核指标体系构建[J].水利科技与经济,2013(5):47-50.
[8]王树鹏,张云峰,朱武.云南省区域和行业用水效率考核体系构建研究[J].中国农村水利水电,2011(10):62-65.
[9]刘晓,刘虹利,王红瑞,等.北京市水资源管理“三条红线”指标体系与评价方法[J].自然资源学报,2014(6):1017-1028.
[10]CHEN C,HAN J,FAN P.Measuring the level of industrial green development and exploring its influencing factors:empirical evidence from China’s 30 provinces[J].Sustainability,2016,8(2):153-154.
[11]FILHO S.Labour market and turnover in the industrial employment in the Brazilian Northeast region[J].Investigación Económica,2016,295 (75):203-230.
[12]张峰,薛惠锋,王海宁.基于幅度随机前沿的工业水资源利用效率测度[J].华东经济管理,2017(1):74-82.
[13]姜蓓蕾,耿雷华,卞锦宇,等.中国工业用水效率水平驱动因素分析及区划研究[J].资源科学,2014(11):2231-2239.
[14]余维,汪奎,赵远翔.我国工业用水效率研究进展[J].人民长江,2012(S2):70-74.
[15]CARVALHO P,MARQUES R C.Estimating size and scope economies in the Portuguese water sector using the Bayesian stochastic frontier analysis[J].Science of The Total Environment,2016,544:574-586.
[16]SUN C Z,CHEN S,ZHAO L S.Spatial correlation pattern analysis of water footprint intensity based on ESDA model at provincial scale in China[J].Journal of Natural Resources,2013,28(4):571-582.
[17]NUTTLI O W.Seismic wave attenuation and magnitude relations for eastern North America[J].Journal of Geophysical Research,1973,78(5):876-885.
[18]章恒全,张陈俊,张万力.水资源约束与中国经济增长——基于水资源“阻力”的计量检验[J].产业经济研究,2016(4):87-99.
