金属板材拉深过程的数值模拟研究

娄用够

（宁波职业技术学院，浙江 宁波 315800）

拉深工序是板料冲压基本工序之一，在拉深过程中，板料发生变形区域较大，受力情况比较复杂，材料应变较剧烈，因此在拉深过程中，板料容易发生起皱、拉裂等缺陷。对拉深过程中板料的变形问题进行了大量的研究工作，也取得了一些有意义的成果。近年来，随着计算机技术的发展，有限元技术在板料冲压成形的研究中得到了越来越广泛的应用，采用有限元方法模拟金属板料的成形过程，可根据成形过程中各部分的受力情况的不同，预测板料可能出现缺陷的位置，从而可根据预测结果在制订拉深成形工艺和设计模具时，采用相关的措施来避免拉深成形过程中出现的各种缺陷。很多学者也采用有限元技术对板料成形过程进行了大量的数值模拟研究。卢曰杨等人对奥氏体不锈钢变薄拉深过程进行了二维的数值模拟分析。王元勋等人进行了矩形盒拉深成形的数值模拟与实验研究。刘晓晶等人对平底筒形件主动径向加压充满液拉深的数值模拟。孙云泽等人对马达壳拉深工艺进行了数值模拟分析。安小军等人基于ANSYS软件进行了板料拉深数值模拟研究。

本文以20号钢的板料拉伸过程为研究对象，通过建立三维有限元模型对拉伸过程进行了数值模拟，获得了板料的变形过程，并对拉深过程中的冲压力及板料的应力分布情况进行了详细的分析。

1 三维模型

板料拉伸过程的三维几何模型如图1所示，其中金属板料的厚度为2mm。板料拉伸过程的有限元模型如图2所示。拉深凸模、拉深凹模和金属材料均采用八节点六面体双线性热力耦合单元划分有限元网格。在金属板料拉深数值模拟过程中，凹模被约束住底面的6个自由度，而凸模则以给定的速度向下运动。拉深凸模、凹模及金属板料在数值模拟时的初始温度被设为室温。

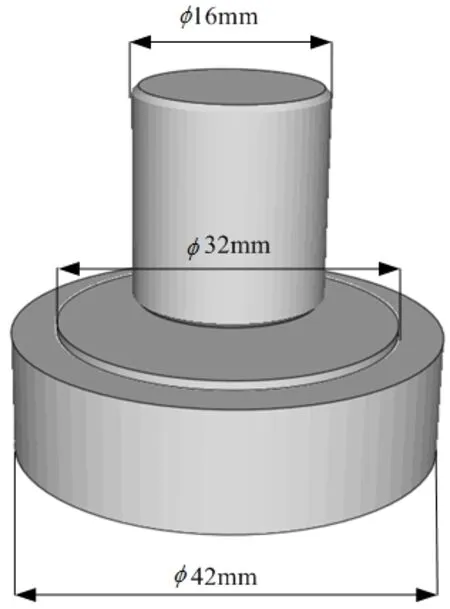
图1 拉深模拟的几何模型

图2 三维有限元模型

2 材料模型

材料的本构关系反映材料物质本性的变化，材料模型是板料拉深过程数值模拟的关键因素。数值模拟过程中，凸模和凹模采用的金属材料相对于金属板料，强度大许多，因此，为了提高有限元的计算效率，凸模和凹模在数值模拟过程中均设置为刚体。而材料为变形体。由于板料拉深过程是大变形过程，而Johnson-Cook模型是一种用于描述金属在大变形、高应变率效应和高温条件下的本构模型，材料的Johnson-Cook方程如下：

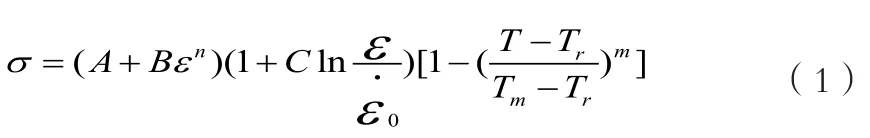
式中：A为准静态下的屈服强度；B为应变硬化系数；n为应变硬化指数；C为应变率敏感系数；m为温度敏感系数；Tr为参考温度；Tm为熔点温度； 为参考应变率。本文中拉深板料选择为20号钢，20号钢的Johnson-Cooks模型中的五个系数值取自文献，其中，A为258MPa，B为329MPa，n 为 0.235，C 为 0.014，m 为 0.804。

3 摩擦与接触边界条件

金属板料的成形加工完全是靠作用于板料的接触力和摩擦力来完成,是一个十分复杂的接触过程,成形过程中钣料与模具之间不断接触与分离,产生相互引导和约束,使钣料最终成形,目前有限元软件中常采用的接触算法有拉格郎日乘子算法（Lagrange）和罚函数法(Penalty Method)。拉格郎日乘子算法(Lagrange)不允许接触边界的相互穿透，与显式算法不相容；罚函数法(Penalty Method)允许相互接触的边界产生穿透,边界穿透量和接触力通过罚因子联系，比较适合于显式算法。另外，罚函数法可以有效的节省计算机内存，提高计算精度,允许划分较细的网络，由此可见，罚函数法比拉格郎日乘子算法更具吸引力。因此，本文中20号钢拉深数值模拟过程中的接触算法即是采用的罚函数法进行接触计算分析。

金属板料的拉深成形加工的数控模拟过程中，所采用的摩擦条件为库仑摩擦定律，板料和凸模之间的摩擦系数为0.2，板料和凹模之间为0.06。在金属板料拉深成型的数值模拟过程中凸模分别给定了3种冲压速度进行了模拟，即 1m/s、2m/s、3m/s、4m/s。

4 数值模拟过程分析

采用有限元软件ABAQUS的显式算法模块（Explicit模块）对20号钢的板料拉深过程进行了数值模拟。

4.1 应力分析

图3、4、5、6分别为拉深模拟过程中当凸模采用2m/s的冲压速度时，各阶段的金属板料上的应力分布及拉深状态。图3是凸模刚接触板料时的状态。图4、5是凸模进入凹模中时的状态，由于拉深过程中，板料没有压边圏的限制，板料周边发生了很明显的起皱现象。图6是板料拉深后的应力分布。由图可知，板料的侧壁由于受到拉深作用而变薄，侧壁的变形比较严重，因此，侧壁上的应力值也最大，这与实际板料拉深过程中侧壁应力最大相符合，也验证了所建立的有限元模型的正确性。

图3 凸模刚接触板料时的应力状态

图4 板料发生明显的起皱现象

图5 侧壁成形后的状态

图6 拉深板料最后的应力状态

4.2 应变分析

图7为20号钢拉深结束时板料的模拟结果，图中显示的状态变量为等效塑性应变。从图中可以看出，在板料的侧壁上，应变率达到了1×101/s。但在板料其它区域的应变、应变率均明显低于侧壁区域，说明板料侧壁发生的变形较大。

图7 板料的应变

4.3 冲压力分析

图8也是凸模采用冲压力的变化曲线，由图可知，随着凸模的向下运动，在凸模接触板料后，冲压力逐渐增加，当板料的侧壁开始变薄到一定程度，冲压力达到最大值，然后，随着凸模的继续向下运动，冲压力逐渐减小。

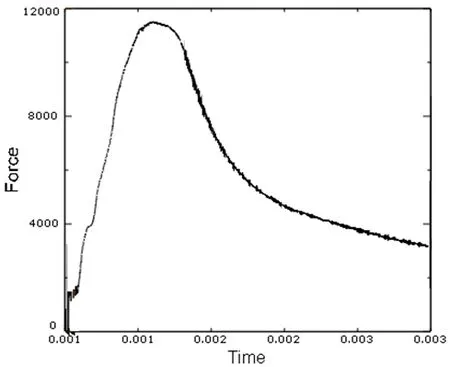
图8 拉深过程中的冲压力曲线

图9为不同冲压速度下最大冲压力的曲线。由图可知，对于20钢的板料的拉深变形过程，随着冲压速度的增加，最大的冲压力增加，凸模的速度超过3m/s后，最大冲压力又开始下降。

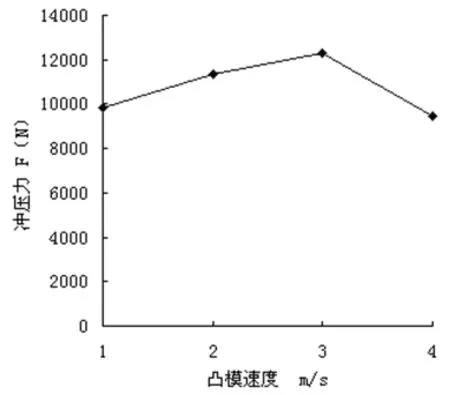
图9 不同冲压速度下的最大冲压力曲线

5 结语

建立了用于板料拉深过程数值模拟的三维有限元模型，采用有限元软件ABAQUS显示算法模块对20号钢的板料拉深成型过程进行了数值模拟研究。通过数值模拟研究了板料在拉深过程中的变形情况，并对20号钢拉深成型过程中的冲压力及板料上的应力分布进行了详细的分析。

参考文献：

[1]卢曰杨，王雷刚，黄瑶.奥氏体不锈钢变薄拉深过程的数值模拟 [J].Die and Mould Technology,2008,(2):40-43.

[2]王元勋，王书恒，沈为，李荣峰.矩形盒拉深成形的数值模拟与实验[J].华中科技大学学报，2006，34（12）:80-82.

[3]刘晓晶，徐永超，苑世剑.平底筒形件主动径向加压充满液拉深的数值模拟[J].Materials science & Technology,2008,16(6):763-767.

[4]孙云泽，薛克敏，王可胜，董定褔.马达壳拉深工艺分析及数值模拟 [J].Die and Mould Technology,2005,(4):34-37.

[5] 安小军,谢桂兰,刘新.基于ANSYS/LS2DYNA的板料拉深数值模拟研究[J].现代制造工程,2007，(1):66-69.

[6]Johnson,G.R.,Cook,W.H.,1983,A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures,Proc.7th Intl Symp. On Ballistics, the Netherlandspp.541-547.

[7]范志强，高德平，覃志贤.20号钢的冲击拉伸力学性能试验研究[J].燃气涡轮试验与研究，2006,（4）:35-37.