一道竞赛试题的解法探究
2018-05-07江苏省无锡市辅仁高级中学214123
中学数学研究(江西) 2018年4期
江苏省无锡市辅仁高级中学 (214123)
耿少峰
1 试题再现
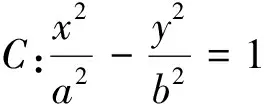
本题是2016年全国高中数学联赛江苏赛区的初赛试题,考查了直线方程、椭圆的标准方程、距离公式以及用代数方法解决几何问题的基本思想.从阅卷的结果来看,得分较低,完全做对的很少,很多学生方法正确但是算不出结果.本文就这道题的解法进行探究分析.
2 解法探究
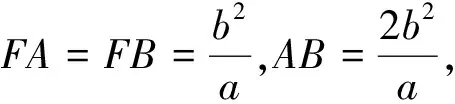


点评:此解法是常规解法,但是需要学生有较强的运算能力.大部分考生使用的就是这种方法,很多学生能够通过特殊情况计算出离心率,但是对一般情况而言,很少有学生能计算到最后.

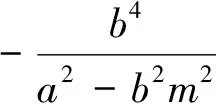
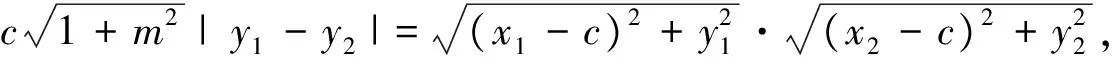
点评:根据直线过右焦点,将方程设为x=my+c,不仅避免了斜率的讨论,更减少了运算量,问题解决起来更加容易.

点评:使用第二定义表示AF、BF更加容易,形式更加简洁,更容易得到正确的结果.


点评:设点坐标也是解决此类问题的常用方法,但是难点在于寻找各个量之间的联系,列出相应的关系式,对思维能力的要求比较高.
解法5:由题意知,双曲线的右焦点F(c,0),设直线l的倾斜角α,直线l的方程为

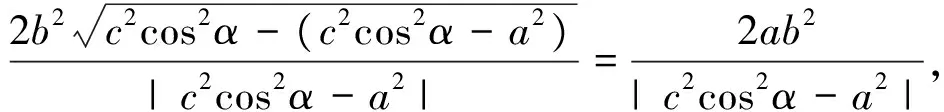
点评:本题使用参数方程去解大大减少了运算量,使问题变得容易了许多.
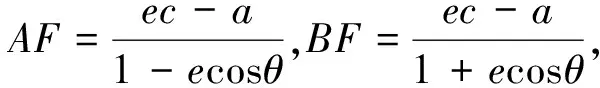
点评:角参数焦半径公式在常规解题中使用的并不多,但是在解决此类问题的时候能够大大减少运算量,使问题得到有效的解决.
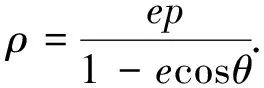

点评:建立极坐标系,进一步减少了解题过程和运算量,使问题更加容易解决.
3 反思
解析几何的问题通常运算量较大,学生容易望而生畏,让学生学会从不同的视角去解读,往往能使他们有不一样的收获.解决问题的角度并不是一朝一夕就可以发现的,需要长期的积累、总结、反思才能完成.总之,问题的解决固然重要,但是解决之后的反思应当更加重视.从不同的角度去重新审视一道题目能够拓宽自己的视野,从而避免成为“井中之蛙”.
