数学课堂上的“自生型探究”
——一节试卷评讲课上的意外收获
2018-05-07江苏省徐州市铜山区棠张中学221113
江苏省徐州市铜山区棠张中学 (221113)
孙安玉
数学教学要培养学生的质疑能力和探究能力,课堂上的质疑和探究活动往往都是教师有目的的课前预设,而课堂上通过学生的自主学习和小组合作学习往往会有些意外的、自主生成的质疑和探究,笔者将其称为“自生型探究”,它是一种超出预定的、自发性的、更深入的问题的提出、分析、解决、总结和拓展的活动.下面结合笔者执教的一节试卷评讲课所出现的教学片段谈一谈,不当之处请批评指正.
题目江苏省南通市2015届高三上学期期末考试数学试题17:
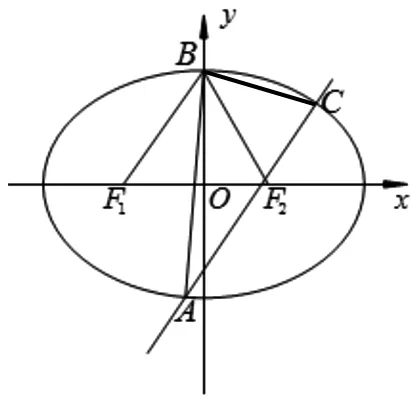
图1

(1)求椭圆的方程;
(2)过右焦点F2的直线与椭圆交于A,C两点,记△ABF2,△BCF2的面积分别为S1,S2.若S1=2S2,求直线的斜率.
同学们首先结合自己的情况进一步思考、然后在小组内讨论本题解决的途径,并由代表展示.
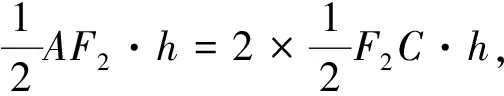
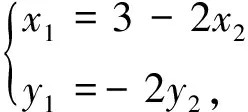
生A继续评价:1.利用向量在解析几何中的作用找到A,C的关系;2.也可以将x1,y1用x2,y2表示构建方程.
生B:我的解法也用到了向量,但是我没有代入椭圆方程,而是用圆锥曲线的统一定义:
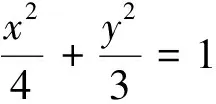
生B继续评价:1.本题出现了焦点弦(两个焦半径),所以想到了圆锥曲线的统一定义;2.统一定义中能找到横坐标或者纵坐标的直接关系.

图2
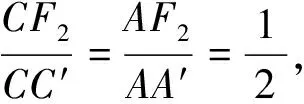
生C继续评价:1.结合统一定义达成焦半径的转化;2.利用Rt△求解更优化.
笔者感觉特别欣慰,给三位同学以高度的评价,正要继续下面的内容,这时“意外”出现了.
生D:对于同学C的解法很赞同,但是我想提出一个问题,在Rt△CAH中知道焦点分弦的比,可以求出直线的斜率.反过来,如果知道了直线的斜率是不是也可以求出焦点分弦的比呢?
这个问题出来后,笔者顺势把问题抛给了学生(毕竟老师也需要思考一下),同学们探究一下D同学的问题,看哪一组可以给出答案?经过一段时间的自主思考后同学们在小组内讨论了起来(笔者也深入各组了解情况,参加讨论),又有如下的展示过程.

师:很好!同学E抓住了圆锥曲线的定义和Rt△CAH灵活的进行了两者之间的转化,请坐.但是生E不愿坐下又提出了:如果我们知道了直线的斜率和焦点分弦的比值能不能求出椭圆离心率呢?这又引起了下面同学的热议.
生F:是可以的,因为在Rt△CAH中涉及到了三个量:直线的斜率(倾斜角)、椭圆的离心率、焦点分弦的比值.利用统一定义知道其中两个就能求出第三个.
比如知道直线的斜率为1,AF2=2F2C,有以下过程:

生F又问道:1.对于双曲线和抛物线是不是也有类似的结论呢?有没有离心率、比值、斜率(倾斜角)的一个通式?
2.对于过左焦点F1的直线与椭圆交于A,C两点也有同样的结论吗?
3.焦点在y轴上又有什么样的结论呢?
经过组内的热烈讨论后形成了以下成果:
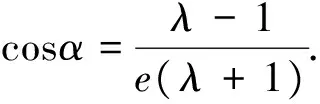
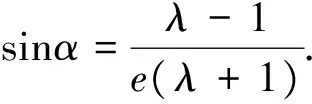
此时下课的铃声响起来了,笔者本节课的教学任务因“意外”没有完成,但是通过学生的自主质疑和探究对这类题深入已经让教者惊叹,“自生型探究”让课堂焕发出了别样的精彩.
俗话说“授人以鱼不如授人以渔”,数学课堂上,教师要敢于放手、给学生更多的空间、鼓励学生大胆的质疑、利用学生互助的能量、开发学生自研自探的能力,让学生的思维走向深入,才能让“自生型探究”的课堂常态化,从而使课堂教学得到最大化的收益.
