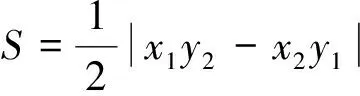三角形面积公式的多种证法及应用

浙江省金华市第六中学 (321000)

虞 懿

浙江省丽水中学 (323000)

曹 斌

1 证法举隅

证法1(平面向量法)：

思考：本证法是最常见的证明方法，但计算量是比较大的．

思考：上述证法是运用空间解析几何的向量积，虽然这是个平面问题，但是平面也是空间的一部分，这也充分说明向量积在处理某些面积问题时是有优势的.

图1

考虑到A,B两点坐标可以互换，所以SΔAOB=

思考：对面积进行合理割补，从而构成我们所熟悉的图形面积问题进而解决，这是很常用的方法．

思考：几何问题转化成代数运算，用点到直线的距离以及最常规的面积公式解决问题．

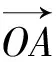
2 应用举隅

(1)求点A,B的坐标；(2)求ΔPAB的面积．

解：(1)由直线PA的斜率存在，设切线PA的方程为y=k(x-t)(k≠0).联立方程

由Δ=16k2-16kt=0,解得k=t.当k=t时，由x2-4kx+4kt=0,解得x=2t.所以点A的坐标为(2t,t2).

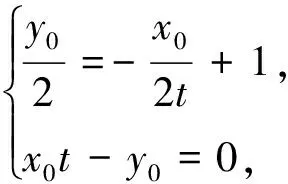
评注：利用三角形面积公式的坐标表示来求解问题(2)，避免了对边长和高的计算，简化了解题步骤，让学生体会到数学的简洁美.

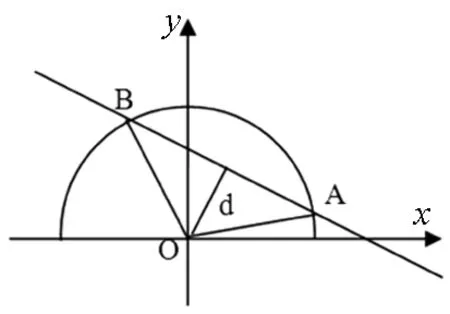
图2

解：如图2所示，设A=(cosα,sinα),B=(cosβ,

评注：利用三角形面积的坐标公式求解关键在于确定三角形各点的坐标．

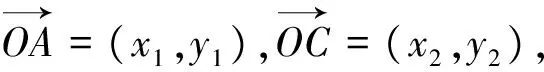
评注：本题的解法多种多样，但运用三角形面积公式的坐标形式解决，可使思路清晰，过程优化．

例4 (2011河南省高中数学竞赛第11题)在平面直角坐标系xOy中，以原点O为圆心，分别以a,b(a>b>0)为半径作两个圆．点Q是大圆半径OP与小圆的交点，过点P作AN⊥Ox，垂足为N,过点Q作QM⊥PN,垂足为M,记当半径OP绕点O旋转时点M的轨迹为曲线E.

(1)求曲线E的方程；

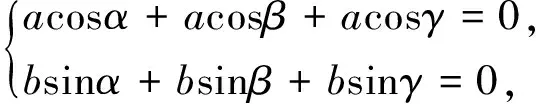
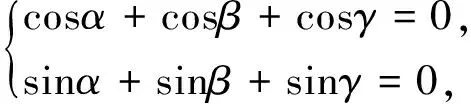
评注：这里应用三角形面积的坐标公式及用椭圆的参数方程形式表示椭圆上的点的坐标，将已知条件转化为三角函数求值问题，避免了复杂的运算．从而使解题过程清晰流畅，令人赏心悦目，流连忘返．

从以上数例可以看出，运用三角形面积公式