沿岸建筑物对VTS雷达的遮蔽影响

郑元洲， 程小东， 甘浪雄， 周春辉， 高俊杰

(1.武汉理工大学 航运学院， 武汉 430063；2.内河航运技术湖北省重点实验室， 武汉 430063)

沿岸建筑物对VTS雷达的遮蔽影响

郑元洲1,2， 程小东1,2， 甘浪雄1,2， 周春辉1,2， 高俊杰1,2

(1.武汉理工大学 航运学院， 武汉 430063；2.内河航运技术湖北省重点实验室， 武汉 430063)

为研究沿岸建筑物对雷达的遮蔽影响程度，根据建筑物的结构形式特点及其与雷达的相对高度建立遮蔽区域的表达模型；建立坐标系，根据几何关系计算得到遮蔽区范围和高度；基于雷达电磁波绕射理论，计算出遮蔽区的目标发现高度。以太子湾邮船母港建筑物对蛇口雷达的影响为例，运用数值计算模型对遮蔽区域的面积和高度进行计算及可视化，并用实船试验和实船观测加以验证。研究结果不仅可用于分析建筑物对现有VTS(Vessel Traffic Service，VTS)雷达站的影响，还可为拟建VTS雷达站选址提供参考。

沿岸建筑物；VTS雷达；遮蔽；电磁波绕射；实船试验

随着港口的不断发展，沿岸高层建筑物逐渐增多,这些高层建筑物对雷达电磁波有较强的反射特性，会在背离雷达水域形成一定的遮蔽区域，导致船舶交通管理中心(Vessel Traffic Service，VTS)难以实时掌握遮蔽水域的船舶动态，增大了海事监管的难度。因此，就沿岸建筑物对VTS雷达的遮蔽影响开展研究十分必要。

在雷达遮蔽区域的计算方面:母德伟等[1]基于悬索桥的特点，提出相应的计算模型，通过实例分析计算悬索桥对VTS雷达产生遮蔽的面积;周宗伟等[2]研究基于数字高程模型数据的雷达地形遮蔽盲区计算方法，通过明确地形遮蔽点确定雷达的遮蔽盲区，得出雷达在不同高度的探测能力范围;任波等[3]总结雷达盲区的成因，提出数字地图的处理方案，得出一种快速计算雷达地形遮蔽盲区的方法，并通过仿真证明该方法的可行性;吴航[4]提出一种处理图像叠加的方法，能较快地找到遮蔽物体,利用实景图像和雷达图像做叠加处理，快速确定遮蔽物的位置，同时提出一种可判断场监雷达盲区成因的方法;XUE等[5]研究得出基于转盘爬虫对象的盲区计算模型，可快速计算出飞机在低空突防过程中的雷达地形遮蔽盲区，并通过实例计算得出雷达在不同高程下的地形遮蔽盲区分布图及可视化模型。目前针对沿岸建筑物对VTS雷达遮蔽影响的研究较少，传统的研究思路是采用几何光学的方法计算遮蔽区域的大小，存在的问题是仅考虑障碍物的遮挡而没有考虑电磁波的绕射。

在雷达电磁波绕射模型方面:马旭勃等[6]以电磁波绕射为基础提出相应的计算模型，可减少遮挡阴影区的相关计算，降低仿真计算的复杂度;郑灼洋[7]对电磁波的绕射规律进行研究，推导出刃峰绕射和圆顶峰绕射的相应公式，并对多山峰实际地形绕射因子的计算进行相应的研究;郭徽东[8]利用雷达性能参数和雷达绕射理论，对风电机对岸基雷达方位、距离和高度探测的遮挡影响进行定量分析;刘克中等[9]基于雷达绕射理论和性能参数分析雷达回波的特点，研究风电项目对航海雷达的影响。

本文为研究建筑物对雷达的遮蔽影响，建立雷达遮蔽区的数学表达模型，定量计算遮蔽区面积和高度,同时通过实船试验加以验证。研究结果不仅可用于分析已有建筑物对现有VTS雷达的影响，还可用于评估周边沿岸建筑物对拟建雷达站的影响，为拟建VTS雷达站的选址提供重要的理论参考。

1 遮蔽区域的表达

根据建筑物自身的结构形式特点及其与雷达的相对高度，建筑物对雷达遮蔽区域的数学表达方法分为有限连续三维遮蔽区、有限不连续三维遮蔽区、无限连续三维遮蔽区和无限不连续三维遮蔽区等4种。

1.1 有限连续三维遮蔽区表达模型

建筑物结构形式连续，其高度比雷达低，形成的有限连续遮蔽区域的表达模型可用A(x,y,z)来表示。引入雷达遮蔽区边界算法，取雷达坐标为(x0,y0,h)。若假设存在遮蔽始面A1，边界符合函数关系F(x,y,z)=0，取其上一点a1(x1,y1,z1)，雷达发射线过点a1的迹线可表示为

(1)

遮蔽区域的边界面表示为

(2)

则表示有限连续遮蔽区域A(x,y,z)在面A1(F(x,y,z)=0)与面A2(z=0)之间。

1.2 有限不连续三维遮蔽区表达模型

建筑物结构形式不连续，其高度比雷达低，形成的有限间断的遮蔽区域模型可用B(xi,yi,n,z0,z1,…,zn,k1,k2,…,kn)来表示。引入雷达遮蔽区多元组法，取雷达坐标b(0,0,h)，取遮蔽区域在水平投影面上任意一点，假设其坐标为(xi,yi,0)，遮蔽高度为Bin。在遮蔽始面B1(F(x,y,z)=0)与yxi-xyi=0的交点Bn((xB1,yB1,zB1),(xB2,yB2,zB2),…,(xBn,yBn,zBn))上共有n个坐标点，n有限。由于点b,点Bin和点Bn三点共线，因此根据方程xBn/xi=yBn/yi= (zBn-h)/(zn-h)可得到zn。由遮蔽区域高度kn=zn-zn-1可得到B。

1.3 无限连续三维遮蔽区表达模型

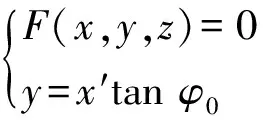
1.4 无限不连续三维遮蔽区表达模型

建筑物自身的结构形式不连续,其高度比雷达高或多个建筑物构成的建筑群形成的无限不连续三维遮蔽区，其模型可结合A,B,C等3种方法来表示。

2 遮蔽区域的数值计算

2.1 坐标系的建立

首先确定遮蔽区的地理范围，根据其大小创建一个恰好能包围该遮蔽范围的矩形R，对于无限遮蔽区,可适当缩小矩形R的面积，制作出包含矩形R、建筑物和雷达的地图。为便于计算，需建立统一的坐标系(见图1)。以雷达基点为坐标原点，以西、南、天等3个方向为坐标轴建立坐标系，其中:O点为雷达水平面基点;O1点为雷达天线发射点;建筑物为任意不规则体，部分高于雷达天线发射点，部分低于雷达天线发射点。

选取某基准面作为xOy基准面，采用北京54坐标系下雷达和建筑物的实际地理坐标值作为x及y的坐标。雷达天线发射点坐标为(X0，Y0，Z0)，建筑物某角点坐标为(X1，Y1，Z1)，当雷达天线发射点的坐标转换为(0，0，0)之后，建筑物某角点的坐标相应地转换为(X1-X0，Y1-Y0，Z1-Z0)。

2.2 建筑物垂直遮蔽线的确定

雷达电磁波在沿直线传播的过程中，建筑物对雷达电磁波产生遮挡，阴影部分为遮蔽区域(见图2)，将图2中的线段PP1和线段QQ1定义为垂直方向上的遮蔽线。

为确定建筑物的垂直遮蔽线，在图1中连接O点和遮蔽区域内任一点H，分别交平面BCC1B1和平面ACC1A1于P点及Q点，再作垂线PP1和QQ1。直线OH在从C点逆时针旋转到A点的过程中，QQ1的高度显然总是大于PP1的高度。只要建筑物处于雷达电磁波垂直照射范围之内，将存在以下2种情况：

1)若直线O1Q1的斜率大于直线O1P1的斜率，即kO1Q1>kO1P1,则遮蔽高度HH1由线段QQ1的高度决定，与斜率是否>0无关,即建筑物垂直遮蔽线为QQ1，H点遮蔽高度为垂线HH1的高度H0(见图3)。

2)若直线O1Q1的斜率小于直线O1P1的斜率，即kO1Q1

2.3 遮蔽高度的几何计算模型

建筑物的垂直遮蔽线确定之后，以雷达天线为圆心，以雷达最大探测距离Rmax为半径，以角度步长Δα为单位划分遮蔽区域，在扫描扇面内确定扫描方向线(见图5)。在每个扫描方向线上从垂直遮蔽线起，以距离步长ΔR为单位向遮蔽区域逐步取点，计算相应点的高度，直到所取点的高度为0或不在研究范围内为止。逐一计算各Δα方向，即可得到遮蔽区域的面积和高度。角度步长Δα和距离步长ΔR越小，计算精度越高。

各点的几何遮蔽高度计算步骤为

1)确定xOy平面内各直线的方程，求得P点和Q点的坐标。遮蔽区域内某点H的坐标为(a，b)，求得射线OH为y=(b/a)x。将xOy平面内各点坐标代入方程，可得直线AB的方程为y=k1x+b1，直线BC的方程为y=k2x+b2，直线AC的方程为y=k3x+b3；联立直线OH和BC(或BA)的方程求得P点的坐标；同理,联立直线OH和AC的方程求得Q点的坐标。

2)确定空间内平面方程。设平面A1B1C1的方程为Ax+By+Cz+D=0，已知A1，B1，C1等3个点的空间坐标，可得平面A1B1C1的方程的系数，从而求得平面方程。将P点和Q点的横纵坐标依次代入平面A1B1C1的方程内，求得P1点和Q1点的空间坐标，就得到ZP1和ZQ1的值。

3)确定垂直遮蔽线之后，求取空间雷达射线方程。在图2中,kO1Q1>kO1P1，此时ZQ1>ZP1，需计算的直线方程为O1Q1。同理,情况二中需计算的直线方程为O1P1。

4)计算几何遮蔽高度。从图3中可看出，当kO1Q1>kO1P1时，ZQ1>ZP1，前面求得O1Q1的直线方程为x/xQ1=y/yQ1=(Z-ZO1)/(ZQ1-ZO1)，将H点坐标(a，b)代入方程，即可得垂线HH1的高度H0。

同理，由图4可知，当kO1Q1ZP2，前面求得O1P1的直线方程为x/xP1=y/yP1=(Z-ZO1)/(ZP1-ZO1)，将H点坐标(a，b)代入方程，即可得垂线HH1的高度H0，即几何遮蔽高度hR。

2.4 基于雷达电磁波绕射理论的计算模型

基于刃峰绕射模型[10]，可对障碍物遮挡雷达电磁波的现象进行分类研究，包括障碍物低于雷达天线高度和障碍物高度高于雷达天线高度2种。当障碍物高度低于雷达天线高度时，障碍物对雷达产生一定的遮挡影响(见图6)。

图6中:hT为雷达天线高度;h为障碍物高度;hR为目标高度，表示当目标在雷达几何地平之内时，目标最高点在雷达和障碍物的连线上。基于绕射理论,当电磁波衰减量A<12 dB时，绕射高度H为

(1)

当障碍物高度大于雷达天线与障碍物连线H长度时，电磁波的绕射衰减量达12 dB，目标将不能被雷达探测到。因此，目标在遮蔽区域内的发现高度H1为

(2)

当电磁波衰减量A=12 dB(即目标的雷达回波不存在衰减)时，绕射高度H为

(3)

即当障碍物高度小于雷达天线与障碍物连线H长度时，电磁波不存在衰减，目标探测不受障碍物的影响。因此，目标在阴影扇形区的雷达回波零衰减高度H2应为

(4)

由此,障碍物的灵敏度降低弧范围为：H1≤hR≤H2。在灵敏度降低弧范围内，目标的雷达回波强度会随着障碍物高度的增大或目标高度的减小而逐渐变弱，直到无法被雷达探测到，进入雷达的探测盲区。

应用建立的计算模型，通过MATLAB编程计算,可得到几何遮蔽高度hR,目标发现高度H1和目标雷达回波零衰减高度H2。几何遮蔽高度未考虑雷达电磁波的绕射；目标发现高度是依据雷达电磁波遇到建筑物遮挡会产生绕射的特性并结合刃峰绕射模型计算出的，表示目标能被雷达探测到所需的最低高度；目标雷达回波零衰减高度表示目标雷达回波不受建筑物影响所需的高度，对飞行物有较大的指导意义，对在遮蔽区域内航行的船舶的指导意义不大。

逐一计算各Δα方向上全部点的目标发现高度，可得出遮蔽水域范围的目标发现高度。采用该计算模型计算建筑物对雷达造成的遮蔽区域的高度和面积。

3 实例研究

3.1 数值计算

蛇口雷达站位于22°28′32″N,113°54′56″E，深圳太子湾邮船母港东北约900 m处，高度为28.38 m，主要用于监管深圳湾水域。邮船母港建筑物由邮船中心和分布于三座突堤上的候船楼组成。邮船中心的最高点高度为67.50 m，最低点高度16.62 m。候船楼建筑的高度为20.30 m。邮船母港规划建设的高层建筑将对蛇口雷达站造成遮挡，在蛇口港池水域形成连续无限三维遮蔽区和连续有限三维遮蔽区。

蛇口雷达站与邮船母港的相对位置关系见图7。首先确定xOy平面内的计算边界，蛇口雷达站O与突堤东南侧码头面顶点E的连线为右边界OM；点O与邮船中心西北侧角点C的连线为左边界ON，则计算水域范围缩小。

将计算结果中的几何遮蔽高度和目标发现高度数据导入到ArcGIS中，叠加在校正好的地图上进行对比分析(见图8)。

蛇口雷达站遮蔽区域范围见图9，连接几何遮蔽高度为零的点和码头岸线可得几何遮蔽区域边界线，连接目标发现高度为零的点和码头岸线可得考虑电磁波绕射的遮蔽区域边界线。从图9中可看出，考虑电磁波绕射情况下的遮蔽面积比未考虑电磁波绕射情况下的遮蔽面积小，两者的差值为虚线围起来的封闭区域，经计算得未考虑绕射情况下的遮蔽区域面积约为1 066 798 m2，考虑绕射情况下的遮蔽区域面积约为973 090 m2。

3.2 实船试验验证

为验证遮蔽区域的边界，选取某海巡艇进行实船试验。试验船从二湾附近水域的起点出发，航向为060°，航行至转折点之后再向左转约090°，终点为三湾附近的泊位。试验船航速维持在2～3 kn。从航行路线中可看出，试验船雷达回波信号消失的位置理论上是遮蔽区域的边界。将试验船轨迹图与雷达回波图像相对比,结果见图10。由图10可知，试验船的雷达回波轨迹与航行轨迹一致。

由图10a)可知,初始时刻试验船雷达回波可被发现，没有受到建筑物的遮蔽影响。由图10b)可知,试验船在航行一段时间之后，其雷达回波仍可被发现，此时试验船仍未进入遮蔽区域。由图10c)可知,当试验船向左转约90°航行一段距离之后，其雷达回波突然消失，说明试验船已进入遮蔽区域，试验船雷达回波消失的点即为遮蔽区域的边界。由图10d)可知,在试验船航行到三湾泊位附近水域的过程中，试验船雷达回波一直未被观测到。这是由于试验船已进入建筑物形成的遮蔽区域，且航行路线横穿遮蔽区域。遮蔽区域内目标发现高度为7～8 m(由候船楼形成)和28～107 m(由邮船中心形成)，加上基准面与实际水位的差值0.22 m，实际水面上的遮蔽区域高度为7.22～8.22 m和28.22～107.22 m。试验船水面上高度约为3 m，远小于水面上目标发现高度。因此，试验船进入遮蔽区域之后，其雷达回波一直未能出现。

从图10中可看出，试验船雷达回波消失点与计算模型得出的遮蔽区域的边界相近，实船试验结果与计算结果相吻合。

为进一步分析邮船中心建筑物对蛇口雷达站的遮蔽影响，在深圳VTS中心对遮蔽区域内正常航行的船舶进行实船观测，筛选出拖船“SHE GANG 6 HAO”自港内驶向港外的航线(见图11)。“SHE GANG 6 HAO”长为36 m，宽为10 m。

为验证考虑绕射时的计算结果，将观测船舶雷达回波大小不变的点与计算得出的遮蔽区域相对比，结果见图12。

船舶在穿越遮蔽区域的过程中，当其航行到不受建筑物遮蔽影响的位置时，其雷达回波的大小将不再发生变化。从图12中可看出:船舶雷达的回波从变大到不再变化的区间，目标发现高度为零，船舶航行不受建筑物遮蔽的影响，刚好与实船观测结果一致；此时的几何遮蔽高度仍不为零，受建筑物的遮蔽影响，船舶的雷达回波应是慢慢变大的，与实船观测结果不相符。对比结果表明,考虑电磁波绕射的计算结果更为精确,更贴合实际。

4 结束语

1)根据建筑物的结构形式特点和与雷达的相对高度，建立4种遮蔽区域表达模型。同时,构建建筑物对雷达遮蔽区域的计算模型，并以太子湾邮船母港建筑物和蛇口雷达站为例，对遮蔽区域的目标发现高度和面积进行可视化，验证计算模型的适用性。

2)基于计算模型的结果，通过实船试验和实船观测来验证遮蔽区域边界。实船试验结果表明,计算模型正确,具有一定的工程实用性。

3)针对沿岸建筑物对VTS雷达站的遮蔽影响，海事部门既可采用增设CCTV监控系统和VTS雷达站等措施，也可加强基于AIS数据的监管力度，从而保障港口水域船舶的航行安全。

[1] 母德伟, 黄晓冠, 韩述,等. 悬索桥对VTS雷达信号的影响分析[J]. 交通科技, 2015(3):179-181.

[2] 周宗伟, 熊家军, 江晶,等. 一种基于DEM的雷达地形遮蔽盲区确定方法[J]. 空军预警学院学报, 2013(5):327-330.

[3] 任波, 于雷, 周焘. 一种低空突防的雷达地形遮蔽盲区算法研究[J]. 电光与控制, 2008, 15(1):10-11.

[4] 吴航. 民航场监雷达遮蔽盲区原因的判断方法[J]. 电子制作, 2013(13):125-125.

[5] XUE H T, WANG K B, XIANG X J, et al. Fast Computing of Radar Terrain Masking Blind Space Based on Dial-Reptile Algorithm[J]. Command Control & Simulation, 2011.

[6] 马旭勃, 刘强, 李备. 一种高实时性电磁波绕射仿真模型及其应用[J]. 科技资讯, 2008(34):13.

[7] 郑灼洋. 雷达电磁波遮挡绕射仿真模型及其应用[J]. 舰船电子对抗, 2010, 33(2):104-107.

[8] 郭徽东. 海上风电场对岸基警戒雷达遮挡影响计算分析[J]. 雷达与对抗, 2016(1):6-10.

[9] 刘克中, 张金奋, 严新平,等. 海上风电场对航海雷达探测性能影响研究[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(3):561-564.

[10] 张鸿喜, 韩伟. 电磁波遮挡对舰艇雷达对抗侦察影响分析[J]. 装备学院学报, 2016, 27(3)：120-124.

ShadowingEffectofCoastalBuildingonVTSRadar

ZHENGYuanzhou1,2,CHENGXiaodong1,2,GANLangxiong1,2,ZHOUChunhui1,2，GAOJunjie1,2

(1.School of Navigation, Wuhan University of Technology, Wuhan 430063, China;2. Hubei Key Laboratory of Inland Shipping Technology, Wuhan 430063, China)

High-rise buildings along the coast may reflect radar waves and form a shadow area, which makes it difficult for VTS(Vessel Traffic Service, VTS) to monitor ships in certain sheltered waters. In order to study the influence of coastal buildings on VTS radar, a model of shadowing is established according to the structure characteristics of buildings and the relative height of radar. The coordinate system is set up, and the range and height of the shadow area are calculated according to the geometric relation. The diffraction of radar beam and the target height are taken into account. The influence of the Prince Bay Cruise Terminal Building on Shekou radar station is examined to verify the calculation. The results show that the calculation can make satisfactory prediction.

coastal building; VTS radar; shadowing; electromagnetic wave diffraction; field test

2017-10-18

国家自然科学基金(71372202;51479157;51579202;51679182)；湖北省自然科学基金面上项目 (2014CFB856)；中央高校基本研究经费(2015IVA042)

郑元洲(1979—)，男，湖北监利人，副教授，甲类一等船长，硕导，博士，研究方向为智能航海、船舶智能控制技术。E-mail: zhengyuanzhou0909@163.com

甘浪雄(1969—)，男，湖北咸宁人，教授，硕导，博士，研究方向为船舶航行安全保障技术。E-mail: glx701227@163.com

1000-4653(2018)01-0001-06

U675.74

A