基于ADAMS包装机封口机构的仿真分析

2018-05-07曾祥丹

现代商贸工业 2018年13期

曾祥丹

(北京京东方光电科技有限公司，北京 100176)

1 引言

现代社会的生活水平不断提升，消费者对商品包装美观和质量要求也越来越高。目前我国的包装机与国外先进的包装机相比，我国的包装机还有一定的差距。因此，对包装机的研究有着重要的意义。

包装机可以实现商品包装的自动化生产，完全替代了传统的手工包装，提高了生产效率。而封口传动机构是包装机的关键部件，采用美国机械动力公司开发的ADAMS分析软件，对包装机传动机构的运行动态特性进行模拟仿真，在模拟仿真过程中需要考虑不同的影响因素，需要建立的仿真模型也有所不同，不同的模型对模拟的输出结果影响比较大，因此我们选取设计方案中最接近实际工况的设计模型和动力参数进行仿真分析，输出结果为后续物理样机设计和制造提供理论依据。

2 建立虚拟样机模型

在SolidWorks中建立包装机封口传动机构模型，检测无机械干涉后，把建立完成的传动系统机构模型导入到ADAMS 中。在ADAMS中设置零件材料和运动约束：(1)伺服驱动轴和其上凸轮做布尔加运算、封刀夹爪组件1和其上零件做布尔加运算、封刀夹爪组件2和其上零件做布尔加运算。(2)选取伺服驱动机构、封刀夹爪组件1和2、芯轴等材料均为合金钢。(3)给芯轴添加固定副(fixed joint)，使芯轴与地位置固定，其他组件能绕其转动。(4)封刀夹爪组件1和2与芯轴之间分别添加旋转副(revolute joint)，使封刀夹爪组件1和封刀夹爪组件2只能绕芯轴转动。(5)封刀夹爪组件1和2末端的滚动轴承与对应夹爪之间分别添加旋转副，使滚动轴承只能绕夹爪末端圆孔轴线转动。(6)给伺服驱动轴添加旋转副，使伺服驱动轴只能绕自身轴线运动。(7)在凸轮与滚动轴承之间添加实体接触副。最后在伺服驱动轴上添加驱动(初步设置为660°/s)，各个运动副及驱动如图1所示。

在ADAMS 软件中,设置的碰撞力计算公式为：

STEP为阶跃函数；

x是一个变量，表示距离的大小；

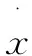
x1表示位移x的自由长度；

e表示力的变形特性指数；

Cmax表示最大阻尼系数；

d表示在施加全阻尼时的边界穿透量。

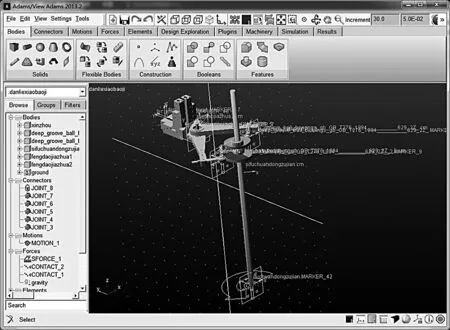
图1 包装机封口传动系统虚拟样机模型

3 接触力计算

如图2所示, 当两物体的距离到达X1时，两物体开始接触，产生碰撞。两物体接触后会产生弹性(或刚性)力和阻尼(或粘性)力。穿透量大小与刚性力关系密切，刚性力越大，穿透量越大。穿透速度的大小与阻尼力的大小有关，阻尼力越大穿透速度越小。接触力、碰撞力大小取决于k、(x1-x)、e、C和C最大时的变形距离d。两物体的材料和结构形状决定了k的大小，k计算公式如下：

根据赫兹接触理论，k计算公式中的R，E*计算方法如下：

1/R=1/R1+1/R2

R1，R2——凸轮和滚动轴承接触点的当量半径；

γ1，γ2——凸轮和滚动轴承材料的泊松比；

E1，E2——凸轮和滚动轴承材料的杨氏模量；

K——刚度系数；

(x1-x)——变形量；

e——碰撞指数；

C——阻尼系数。

图2 ADAMS碰撞力模型

根据设计，伺服驱动轴转速为n=110r/min。凸轮与滚动轴承材料均为40Cr，淬火处理，齿面硬度为40-45HRc。

查机械设计手册得，材料40Cr弹性模量E=2.06e11Pa，泊松比γ=0.3。

所以E1=E2=2.06e11Pa，γ1=γ2=0.3。

根据设计，R1=37mm，R2=13mm。

由赫兹接触理论计算出R=9.62mm，E*=1.13e11Pa。

另外，根据材料特性，查表后，取碰撞指数e=1.5，阻尼系数C=50N·S/mm，渗透深度d= 0. 1mm。由于运动过程中会有摩擦,但凸轮啮合处有润滑，所以相关参数选取如下：动摩擦系数为μk=0.05,动临界速度值Vd=10mm/s，静摩擦系数为μs=0.08，静临界速度值Vs=0.1mm/s。

4 仿真结果分析

在ADAMS中进行仿真和分析时，为了避免启动时的冲击造成的速度突变现象，采用STEP函数，使主动齿轮的转速在0.1s内由0增加到110r/min(即660°/s)，即STEP(time, 0, 0d, 0. 1, 660d)(time为时间自变量)。根据以上计算数据对接触力进行参数设计，根据对封口负载的计算，在封口处添加外力：F =100N。仿真时间取1.5s, 步长取10000。

由分析得到：图3(a)凸轮角速度、(b)封刀夹爪角速度。

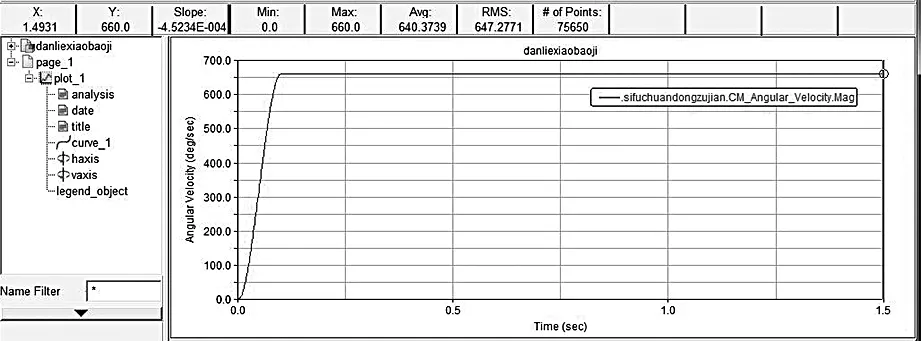
(a)凸轮角速度

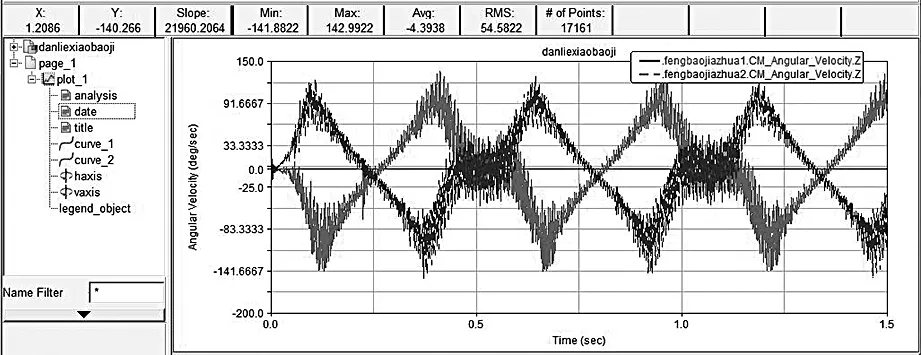
(b)2个封刀夹爪角速度

(1)从角速度方向看，封刀夹爪1起始角速度值为负，封刀夹爪2起始角速度为正，两夹爪角速度曲线大小基本相等方向相反，满足两个封刀夹爪对称运动关系。

(2)从传动机构角速度大小上看，凸轮角速度在0到0.1秒内加速到660 deg/sec，然后匀速转动。符合设计值。封刀夹爪1和2在仿真开始的瞬间,角速度曲线有一个波动, 从0突变到30deg/sec。在0到0.1s的加速阶段，封刀夹爪1角速度平稳上升到141.88deg/sec，封刀夹爪2角速度平稳上升到142.99deg/sec，角速度增加保持对称状态，同时基本符合夹爪开合角142°的预设值，由于间隙震动等引起的误差在可接受范围内。曲线在0.1s到0.65秒完成一个循环，在0.65s到1.2秒完成一个循环，计算得循环周期为0.55秒，即两夹爪每0.55s开合一次，符合预计0.55s封口一次的设计值。曲线在0.48s到0.58s角速度在0deg/sec上下波动，两夹爪在停止运动状态，符合夹爪处于封口压紧阶段的设计。由曲线可以看出，每个循环周期，都有相同时间的封口压紧阶段，机构运行稳定。

(3)从振动情况看，由于选择了STEP函数，避免了启动时冲击造成的巨大速度突变现象，启动平稳。曲线整体有规律的变化，由于振动影响，角速度在预设值附近上下小幅波动，没有巨大突变，运行基本平稳，在可接受范围。曲线在角速度较小时波动较小，在角速度较大时波动相对较大，符合振动随角速度增加变大的实际情况。

由分析得到：图4滚动轴承角速度。滚动轴承在本机构中是惰性轮，没有动力，与凸轮曲面啮合，把凸轮与封刀夹爪的滑动摩擦变为滚动摩擦，减小了摩擦力。曲线在0到0.1s内完成稳定加速，振动较小。符合0.1s到0.65s的循环周期。由于滚动轴承半径较小，转速在2000deg/sec，即5.5r/s，符合设计值。两滚动轴承曲线没有完全重合，是由于振动、机构间隙等原因造成的误差，误差在可接受范围内。

图4 滚动轴承角速度

由分析得到：图5凸轮与滚动轴承接触力。

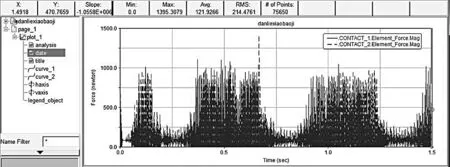
图5 封口挤压力

从时间历程上看，接触力间歇性有规律的变化，符合凸轮廓线分度期与停歇期间歇变化的情况。从接触力曲线可以看出在仿真开始瞬间，接触力曲线有一个较大波动, 从0突变到700N。在0到0.1s的加速阶段接触力平稳逐渐增加到1000N。在0.1s到0.4s内接触力很小，在100N上下波动，此阶段符合2个封刀夹爪处于打开状态，没有封口力存在。在0.4s后2个封刀夹爪开始闭合，接触力瞬间增加到1000N。在0.48s到0.55s内接触力稳定保持在1000N上下，此阶段2个封刀夹爪完全闭合，封口力一直存在，所以接触力稳定在最大值，符合实际情况。封口完成后，2个封刀夹爪逐渐分开，接触力迅速变小，进入下一个封口周期。