基于压缩感知的单像素图像采集技术研究*
2018-05-05吕志强孔庆善薛亚楠
吕志强,陆 云,孔庆善,薛亚楠
(1.中国科学院信息工程研究所,北京 100093;2.中国科学院大学 网络空间安全学院,北京 100049)
0 引 言
图像采集与日常生活息息相关。从日常生活的拍照到电子监控的录像,再到不可见光领域的图像采集,都离不开图像采集与处理技术。传统相机使用银盐感光材料(即胶卷)作为载体,拍摄后的胶卷要经过冲洗才能得到照片,且拍摄过程中无法知道拍摄的效果,不能对拍摄的照片进行删除。后来,数码相机出现在人们的视野。数码相机利用电子传感器把光学影像转换成电子数据。传感器主要利用电荷耦合器件(CCD)或互补金属氧化物半导体(CMOS),拍摄后能即时看到照片效果,也可以删除不需要的照片。此种相机的拍摄质量取决于传感器阵列感光元件的尺寸和像素个数,而这些感光元件都是用半导体硅材料制成的。随着工艺技术的不断提高和硅材料成本的不断下降,高像素的数码相机已经走入千家万户,手机的照相功能也完全可以应付日常的生活所需。
但是,在非可见光领域,硅材料无法感光。此时,CCD或CMOS将无法作为传感器。例如,红外光领域,它的感光材料是铟镓砷,是传统硅材料成本的数十倍。如果依靠增加感光元件的尺寸和个数来提高相机的分辨率,势必会大大增加成本。因此,如何在较少像素的基础上获得较高分辨率值得探讨。此外,传统图像数据采集过程带来了大量冗余,如监控设备对内存的要求很高,但是存储的有用的信息却并不多。所以,通常一段时间后采集的数据会被覆盖,造成信息的丢失。现在的图像视频采集技术都存在采集、存储资源浪费的情况。因此,如何能在保存足够少的数据基础上获得足够多的信息是另一个值得探讨的问题。
本文在压缩感知理论基础上提出了一种单像素图像采集技术,大大减少了数据采集量,具有数据保护、分辨率可调、成本低的特点。本文首先介绍压缩感知理论,然后在此基础上提出基于压缩感知的单像素图像采集技术原理,搭建单像素图像采集的硬件平台,并利用相关算法进行图像重构。
1 压缩感知理论
压缩感知理论的数学模型,如图1所示。

图1 压缩感知数学模型
如果一个长度为N的信号X在某组正交基或紧框架Ψ上的变换系数是稀疏的(即图中的θ是稀疏的,θ=ΨTX),如果用一个与变换基Ψ不相关的观测基Φ:M×N(M<<N)对系数向量进行线性变换,并得到观测集合Y:M×1,那么就可以利用优化求解方法从观测集合中精确或高概率地重构原始信X[1]。
若信号是K,是稀疏的,那么一个与基向量ΨN×N不相干的测量矩阵ΦM×N对信号进行观测,就可以对信号进行压缩,即:

式中,ACS=Φψ称为观测算子,Y=(Y1,Y2,…,YM)是M个观测向量,其中M<<N。这些观测向量含有信号X中的大量信息。对于给定的观测向量Y,若观测矩阵Φ满足有限等距性质(Restricted Isometry Property,RIP)[2]理论,即满足:
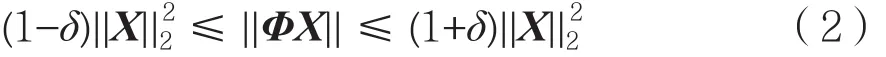
那么,当观测次数满足M≥K×lg(N/K)时,可以通过求解约束最优化问题将N维信号稳定地重构出来。

得到信号的稀疏表示θ,进一步变换,

即:即可精确重构原始信号。
目前,信号的稀疏表示方法包括傅里叶变换、小波变换、正交基字典下的变换、冗余字典下的稀疏分解等。Donoho在文献[3]指出,大部分一致分布的随机矩阵都可作为观测矩阵,如部分Fourier集、部分Hadamard集、一致分布的随机投影(Uniform Random Projection)集等。目前,常用的观测矩阵有随机高斯矩阵、以随机±1元素构成的Rademacher矩阵等。它们都具有高概率恢复原始信号的特性,也具有普适性。关于稀疏信号的重构,目前的信号重构算法大致可以分为四类。第一类是基于求解最小l0范数的贪婪算法,包括匹配追踪算法(MP)、正交匹配追踪算法(OMP)、分级正交匹配追踪算法(StOMP)和正则化正交匹配追踪算法(ROMP)等;第二类是基于求解最小l1范数的凸松弛算法,如基追踪算法、梯度投影系数重建方法(GPSR)和迭代阈值法(IT)等;第三类是统计优化方法,类似于主成分或独立成分分析,利用典型信号的训练集通过学习的方法找出最优的线性投影集合,大致分为贝叶斯统计框架下的稀疏重建算法[4-6]和基于训练集合学习的统计优化方法[7];第四类算法是组合算法,本质思想是针对信号进行高度的结构化采样,主要包括稀疏傅里叶描述法[8]、链追踪(Chaining Pursuit,CP)[9]以及HHSP追踪(Heavy Hitters on Steroids Pursuit,HHSP)[10-11]等。
2 单像素图像采集系统
2.1 单像素图像采集技术原理
单像素图像采集技术建立在压缩感知理论基础上,将原始图像视为信号X,用观测矩阵Φ对其进行观测。观测矩阵的每一行与原始图像的内积为一个观测值,通过光电传感器读取该数值,将该数值传到PC端进行图像的恢复。它的核心元件是具有不同方向偏转的空间光调制器数字微镜阵列(Digital Micromirror Device,DMD)。该空间光调制器由许多小微镜组成,每一个小微镜的内置结构如图2所示。每一个微镜可以向±12°方向偏转,分别代表观测矩阵中的“±1”元素或者“1和0”元素,用传感器接收某一方向的光强得到观测值。

图2 DMD内置微镜结构
该图像采集系统原理如图3所示。待采集图像通过透镜恰好照满微镜阵列,而微镜的每一次变换相当于矩阵的每一行将图像与微镜图案的内积反射给单点传感器,产生相加的效应。DMD翻转M次即完成M次测量,然后将M次测量值通过数据采集到PC端进行图像的恢复。

图3 单像素图像采集原理
根据该原理图,单像素图像采集系统可以分为3个模块,光路调制模块、数据采集模块和图像重构模块。
2.2 光路调制模块
光路调制模块的功能是搭建图像采集系统。首先需要确定图像、透镜以及DMD的相对位置,使得图像通过透镜所成的像清晰照射在DMD上;其次需要调整光电传感器的接收角度,完整地接收DMD某一个方向偏转的全部光强。由于该微镜阵列只有3个方向的偏转,所以观测矩阵应选择只含有“±1”或只含有“0,1”元素的矩阵。目前,满足约束等距性质(RIP)(式2)的矩阵有稀疏二进制随机矩阵、二进制分块对角矩阵和部分哈达玛矩阵等。
2.3 数据采集模块
数据采集模块的功能是利用光电传感器将光信号转换为电信号,再通过采集装置采集电信号。实验中利用光电探测器将光强信号转换为电压信号,再利用模数转换器将电压信号转化为数字信号传送到PC端。
2.4 图像重构模块
观测值被PC端接收后利用图像重构模块来完成最终图像的恢复工作。在这个模块中可以选择不同的恢复算法以达到较好的图像恢复效果。
3 单像素图像采集平台搭建及测试
3.1 单像素图像采集系统硬件组成
依据单像素成像的实验原理,搭建了硬件实验平台,如图4所示。实验光源为手电筒,为了保证光束的均匀性,在光源前加上了Thorlabs公司的散射片。为了调制光路并增加光线的汇聚性,本文选择直径50.8 mm、焦距150 mm的双凸透镜;数字微镜阵列(DMD)选择德州仪器(TI)生产的DMD DLPD4X00KIT套件,包括驱动器、控制器和存储器,阵列大小为768×1 024(实际使用中选择了768×768的阵列,将24×24的阵列看作一小块,得到分辨率为32×32的图像);数据采集模块需要将光信号转换为电信号,本实验采用的是Thorlabs公司生产的型号为PDA10A-EC的光电探测器,具有灵敏度高、抗干扰能力强的优点。因为实验中只能通过观测采集到的数据来判断光路的正确性,并不断调整光路,所以实验数据选用能够实时展现的示波器进行数据采集。

图4 单像素图像采集系统硬件平台
3.2 单像素图像采集系统软件平台
本实验的软件平台主要包括控制DMD加载观测矩阵的上位机程序和数据采集后的恢复平台。图5为控制观测矩阵加载的软件平台,可以改变观测矩阵,也可以控制DMD的翻转速度。图像重构平台可以选择不同的恢复算法处理采集数据,右端实时显示恢复出来的图像。
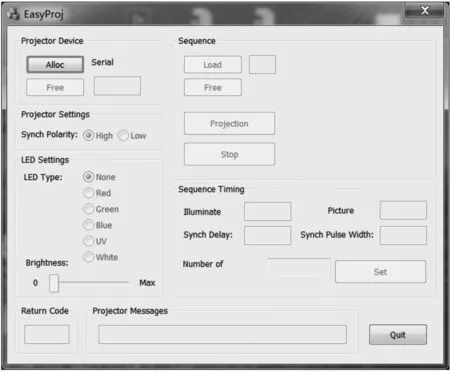
图5 观测矩阵加载平台
实验中采用只含有“±1”元素的哈达玛矩阵作为观测矩阵。哈达玛(Hadamard)矩阵是由+1和-1元素构成的且满足H×HT=NI的N阶方阵。哈达玛矩阵具有正交性,任意两行(列)均正交,因此满足非相关性。
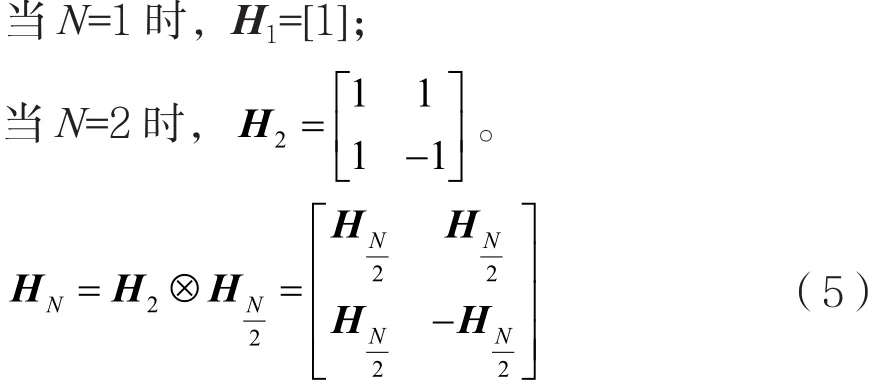
由于DMD只能识别“0”和“1”元素,需要将矩阵中的“-1”元素转换为“0”元素。
构造N×M阶部分哈达玛观测矩阵的方法如下:
步骤1:首先生成一个N×M大小的哈达玛矩阵;
步骤2:从N行矩阵中随机抽取M行;
步骤3:将N×M阶矩阵中的“-1”元素转化为“0”元素。
实验对匹配追踪算法(Matching Pursuit,MP)、正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)以及基于增广拉格朗日和交替方向的最小全变分算法(Total variation Augmented Lagrangian Alternating Direction Algorithm,TVAL3)进行模拟仿真后发现,TVAL3算法具有较快的恢复速度、较高的重构准确率和较强的鲁棒性。因此,选取TVAL3算法作为图像重构算法。该算法的主要思想是在最小全变分算法思想下引入增强拉格朗日和交替方向变换。前者是将带约束的模型转化为不带约束的目标函数,后者用来求解目标函数。
该算法求解如下问题:

其中x是图像信号,Dix表示每个像素横向和纵向的梯度计算,A是感知矩阵,y是通过观测矩阵得到的测量值。
将目标函数转化为增广的拉格朗日函数,得:

其中λ是拉格朗日乘子,μ是障碍参数。通过求解x使得函数LA(x)达到最小值,这里λ和μ是随着迭代而变化的,第K次迭代时记作λk、μk。通过:
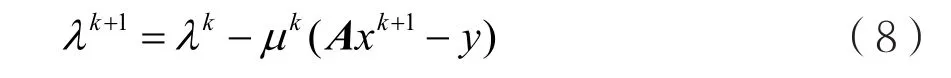
来迭代更新λ的值。
引入凸松弛变量ω,模型变为:

则式(7)变为:
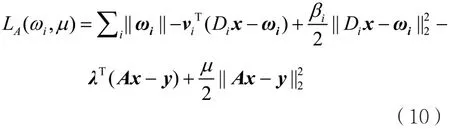
根据式(8),得到:

子问题转化为如何最小化增广拉格朗日函数,也就是要求解以下问题:

显然,式(13)并不是处处可微的,可以通过次微分方程求解。
当||ωi||表示1范式时,有:

当||ωi||表示2范式时,有:
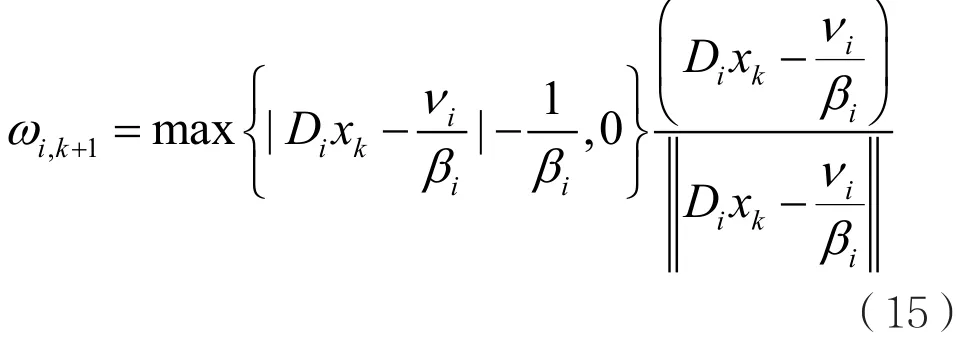
求解次微分方程得到ωi,k+1后,通过计算得到xk+1:
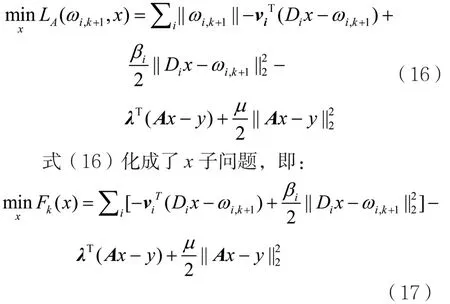
这是一个关于x的二次函数,导数为:

令fk(x)=0,就能得到函数取最小值时的x:
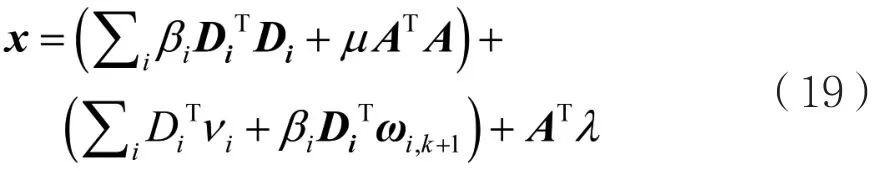
其中( )+代表伪逆矩阵。
根据以上讨论,该算法的步骤如下:
4 实验结果与分析
实验中采用只含有“±1”元素的哈达玛矩阵作为观测矩阵,分别对两个简单的图像“T”和“N”字进行采集,基于在采样率分别为20%、30%、40%、50%时的图像恢复效果如图6、图7所示。

图6 “T”字恢复效果

图7 “N”字恢复效果
实验结果表明,基于压缩感知的单像素图像采集系统是有效的。在采样率只有传统采样像素数的30%时,就能较清晰采集到图像。
图像采集中速度是重要的因素。单像素图像采集时间由观测时间和图像恢复时间两部分组成,即:

其中n观测表示观测次数,f观测表示观测频率。观测频率受到DMD硬件的限制,也受数据传输速度的限制,由式(20)、式(21)得:

表1、表2分别表示“T”和“N”在不同采样率下的图像采集时间,比较文献[12]图像采集速度有了巨大提升,为单像素视频采集技术奠定了基础。
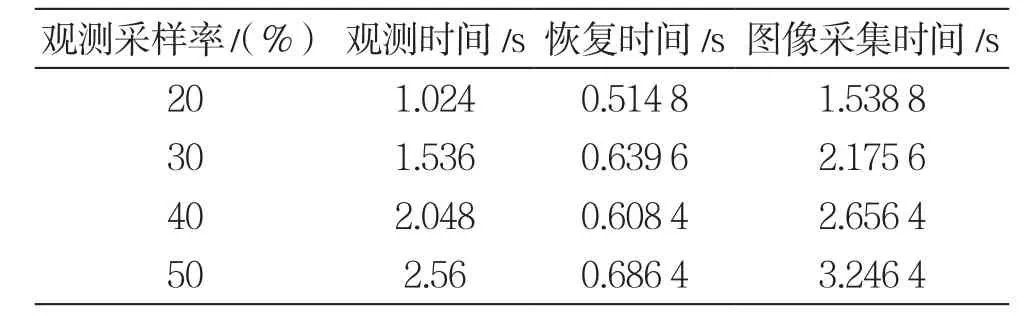
表1 “T”在不同采样率下的图像采集时间

表2 “N”在不同采样率下的图像采集时间
5 结 语
本文利用部分哈达玛矩阵作为观测矩阵,以TVAL3算法作为重构算法,拍摄了两种图像。当测量次数在总像素20%~30%时即可恢复出图形,比传感器阵列节省元件,大大降低了成本,且采集数据量少,有利于存储和压缩。但是,该系统距离实用还有一段距离,需要在尺寸的微型化、拍摄的实施性以及彩色图像的拍摄方面在后续的研究中进行分析。
参考文献:
[1] 石光明,刘丹华,高大化等.压缩感知理论及其研究进展[J].电子学报,2009,37(05):1070-1081.SHI Guang-ming,LIU Dan-hua,GAO Da-hua,et al.Compressed Sensing Theory and Its Research Progress[J].Acta Electronica Sinica,2009,37(05):1070-1081.
[2] Baraniuk R.A Simple Proof of the Restricted Isometry Property for Random Matrices[J].Constructive Approxim ation,2008,28(03):253-263.
[3] Donoho D L,Tsaig Y.Extensions of Compressed Sensing[J].Signal Processing,2006,86(03):533-548.
[4] Zayyani H,Babaie-Zadeh M,Jutten C.Bayesian Pursuit Algorithm for Sparse Representation[C].Proceedings of the IEEE International Conference on Acoustics,Speech and Signal Processing,2009:1549-1552.
[5] Baron S,Sarvoham R,Baraniuk R G.Bayesian Compressive Sensing Via Belief Propagation[J].IEEE Transactions on Signal Processing,2010,58(01):269-280.
[6] Seeger M W,Steinke F,Tsuda K.Bayesian Inference and Optimal Design in the Sparse Linear Model[J].Journal of Machine Learning Research-Proceedings Track,2007,2(06):444-451.
[7] Weiss Y,Chang H S,Freeman W T.Learning Compressed Sensing[C].Proceedings of the 45th Allerton Conference on Communications,Control and Computing Illinois,2007:1-7.
[8] Gilbert A C,Guha S,Indyk P,et al.Near-optimal Sparse Fourier Representations Via Sampling[C].Proceedings of the 34th Annual ACM Symposium on Theory of Computing,2000:152-161.
[9] Gilbert A,Strauss M,Tropp J,et al.Algorithmic Linear Dimension Reduction in the L1 Norm for Sparse Vectors[C].Proceedings of the 44th Annual Allerton Conference on Communication Control and Computing,2006:1-9.
[10] Gormode G,Muthukrishan S.Combinatorial Algorithms for Compressed Sensing[C].Proceedings of the 40th Annual Conference on Information Sciences and Systems,2006:280-294.
[11] Gilbert A,Strauss M,Tropp J,et al.One Sketch for All:Fast Algorithms for Compressed Sensing[C].Proceedings of the 39th Annual ACM Symposium on Theory of Computing,2007:237-246.
[12] 李正炜.基于压缩传感理论的单像素相机成像研究[D].长春:中国科学院研究生院(长春光学精密机械与物理研究所),2012.LI Zheng-wei.Single Pixel Camera Imaging System Based On Compressed Sensing Theory[D].Changchun:Chinese Academy of Sciences(Changchun Institute of Optics,Fin Mechanics and Physcis),2012.
