非高斯噪声下非线性回声消除方法*
2018-05-05杨瑞丽
杨瑞丽,郭 莹
(沈阳工业大学,辽宁 沈阳 110870)
0 引 言
声学回声一直是影响通信质量的关键问题[1-2]。目前,典型的回声消除器的设计是假设回声路径是线性的,可以采用有限长脉冲响应(FIR)滤波器进行建模。然而,近几年,随着低成本的小型设备在免提手机和视频会议等应用中广泛使用,放大器和扬声器引入的非线性回声问题日益严峻[3-4]。这种非线性回声难以由传统的线性回声消除器消除,且回声路径中存在非线性会限制线性滤波器的性能,干扰声学脉冲响应的正确估计,降低语音信号的感知质量[5-6]。因此,如何消除非线性回声日益成为信号处理领域的研究热点[7-10]。
非线性可以粗略分为两种类型:有记忆非线性和无记忆非线性。当扬声器机电系统的时间常数大于采样率时,有记忆非线性通常出现在高质量音频设备中[11],而无记忆非线性则通常出现在移动设备的低成本功率放大器或扬声器中[12]。
以Volterra滤波器为代表的有记忆非线性回声消除方法的权系数数目,会随着记忆长度、阶次的增加而大幅度增多,导致计算量增大,收敛速度减慢,难以得到实际应用。而无记忆滤波器的计算成本很低,且模型设计较为灵活,实际应用将相对便捷。因此,本文采用无记忆非线性滤波器和FIR滤波器的级联结构来建模非线性系统。其中,无记忆非线性滤波器用来模拟非线性器件,而FIR滤波器用来模拟线性声学回声路径。
此外,噪声问题是所有通信系统中无法避免的问题。除了普遍存在的高斯噪声外,在语音信号处理、实时交通检测等环境中,也广泛存在着非高斯噪声[13]。这些非高斯噪声的强冲激性严重影响了基于l2范数优化准则的自适应滤波算法的性能,从而导致采用此类算法的回声消除系统性能退化甚至失效。同时,在免提通话、视频会议等通信场合中存在着回声,其回声路径往往具有稀疏特性,而结合系统的稀疏特性可有效降低算法计算量。因此,本文将文献[14]修正的改进比例归一化最小均方误差(Mdoified Improved Proportionate Normalized Least Mean Square,MIPNLMS)算法中的比例矩阵的思想融合到符号算法(Sign Algorithm,SA)中,提出一种更稳健的新算法,即修正的改进比例归一化符号算法(Modified Improved Proportionate Normalized Sign Algorithm,MIPNSA),并将该算法应用到非线性回声消除系统里的线性滤波器,实现了在各种环境噪声背景下都具有适用性的低复杂度的非线性回声消除方案。
1 级联方案
本文采用如图1所示的Hammerstein模型级联方式,将非线性滤波器和线性滤波器进行级联来实现回声消除。前端的自适应无记忆非线性滤波器用于模拟由放大器与扬声器构成的非线性模型,其后的线性FIR滤波器用于模拟线性声学回声路径。

图1 Hammerstein模型
本文采用的基于Hammerstein模型的无记忆非线性回声消除方案,如图2所示。图2中,x(n)为系统的输入信号,s^(n)为非线性滤波器的输出,也是线性滤波器的输入,y^(n)为线性滤波器的输出,u^(n)为非线性滤波器的输入,a为非线性器件参数,h为线性回声路径,v(n)为背景噪声,d(n)为系统的期望信号。
具体参数如下:
x(n)=[x(n),x(n-1),…,x(n-L+1)]T表示系统的输入向量;


图2 本文采用的无记忆非线性回声消除级联方案
对于无记忆非线性滤波器,本文采取一种级数展开的截断模型来描述,即:
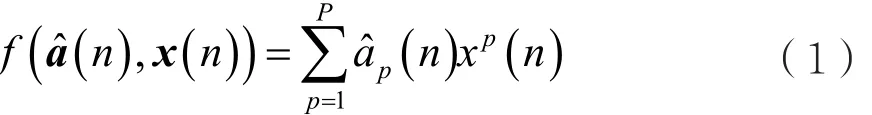
其中,f (a^(n),x(n))表示非线性器件的非线性变换函数,aj( j=1,2…p)为相应n时刻的参数矢量,由实际中扬声器的非线性特性和放大器的输出功率确定。
非线性滤波器的输出s^(n)通过输入xi(n)(i=1,2,…,P)和非线性滤波器参数的线性组合得到。而FIR滤波器的输出
由式(1)可以推导出n时刻对应的非线性滤波器的输出s^(n),即线性滤波器的输入为:

其中:

非线性滤波器的输入向量u^(n)由式(4)表示:

这里:
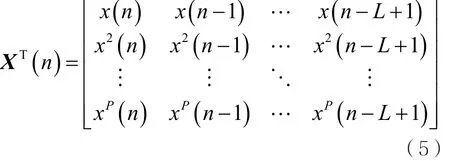
由式(2)、式(3)、式(4)可以得到:

本文所用的两个滤波器的自适应算法采用基于MMSE准则的NLMS算法,分别求取非线性和线性的残余误差能量e2(n)的梯度值。
非线性残余误差能量e2(n)的梯度值为:
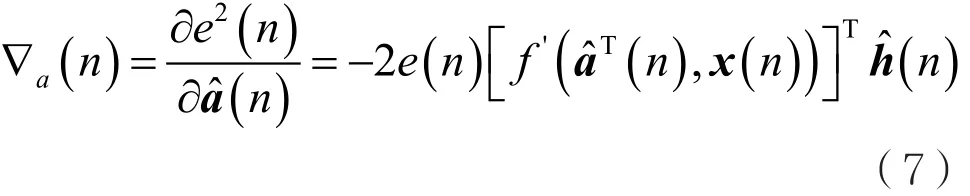
其中,误差信号:

所以,综合式(1)和式(4)可得出非线性滤波器系数的级联NLMS迭代方程:

其中,归一化步长参数为:

φ为一个小的正参量,是为了避免大的步长参数趋于未知方向。
因此,式(10)可以改写为:

相似地,由误差信号e(n)可求得线性残余误差能量e2(n)的梯度值为:

其中,误差信号e(n)=d(n)-h^T(n)s^(n)
所以,线性滤波器系数的迭代方程可以表示为:
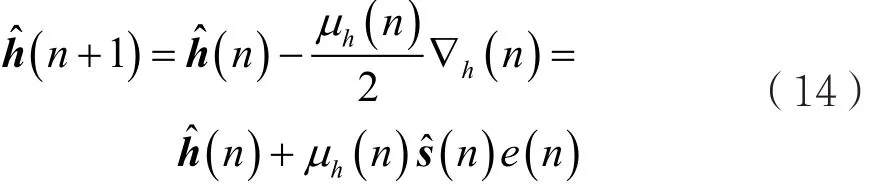
其中,归一化步长参数为:

2 非高斯噪声条件下的新算法
以上所作分析和推导均是在高斯噪声背景下进行的。然而,实际应用中,非线性回声消除系统的背景噪声不一定都呈高斯分布,非高斯噪声同样广泛存在,如由于自然因素(如飓风、宇宙电磁波脉冲、雷电、太阳磁暴、天电干扰等)和人为因素(如报警器、电动机、柴油机、发动机、发电机等)的影响,噪声往往呈现出强脉冲性,其分布比高斯分布具有更厚重的拖尾。这里,本文采用α稳定分布来描述非高斯噪声[15]。
非高斯噪声具有较强的脉冲性,严重影响了基于l2范数优化准则的自适应滤波算法的性能,而符号算法则对脉冲噪声具有很好的抑制效果[15]。同时,考虑到语音通信系统中回声路径的稀疏特性,因此将比例矩阵的思想融入到符号算法中。
在非高斯噪声背景下,已经得到广泛应用的符号算法(NSA)[16]的迭代公式为:

其中,x(n)是系统的输入向量,h(n)是滤波器系数向量,e(n)是误差信号,μ是固定的步长参数。
现有的IPNLMS算法[15]对系统稀疏性具有良好的适应能力,其迭代更新方程为:
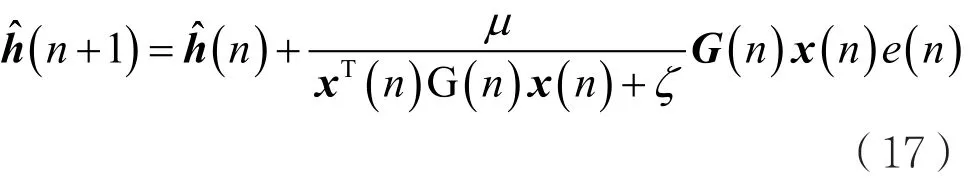
其中,G(n)为IPNLMS算法中的对角矩阵,ζ、φ分别表示正参数。
因此,考虑到回声路径的稀疏特性和非高斯噪声的干扰,将IPNLMS中的系数比例矩阵融入到符号算法SA中,即将式(17)与式(16)相结合,可得到IPNSA算法,其迭代方程为:

其中,G(n)为IPNSA算法中的对角矩阵,ζ、φ分别表示正参数。
由式(17)可知,IPNLMS算法的收敛速度会受到比例项权重的影响,但其比例项的权重与系统稀疏度之间的关系尚不清晰,仍然没有明确的措施来决定该参数值,导致算法性能未能达到最优。而文献[14]通过仿真实验得出一种关于比例项权重与系统稀疏度之间较为明确的关系,提出了一种修正的IPNLMS(MIPNLMS)算法。本文则将该算法中的比例矩阵思想融入到SA中,从而得到MIPNSA的迭代公式。具体分析过程如下。
MIPNLMS算法面对的主要问题是如何将系统稀疏度转化为数值,以便将系统稀疏度与权值的最优值联系起来,进而说明系统稀疏度与比例项权重的最优值之间的关系,而式(19)解决了该问题。
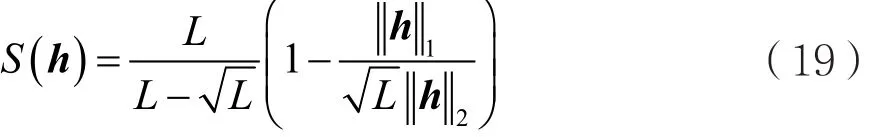
其中,L表示h的长度,||h||1和||h||2分别表示h的L1范数和L2范数,分别定义如下:

S(h)表示系统脉冲响应即回声路径h的稀疏度,数值范围为[0,1]。
S(h)数值的转换可以通过β=(α+1)/2得到,其中α的转换范围是从[-1,1)到[0,1),具体表示为:
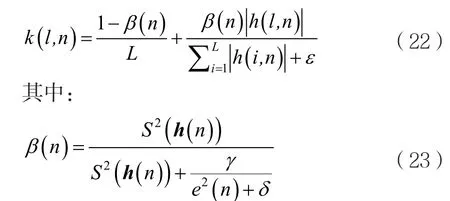
其中,γ和δ分别表示正参数。
由式(19)、式(22)、式(23)可得到该算法中的对角矩阵K(n):

综上可得,MIPNLMS算法的迭代更新方程为:
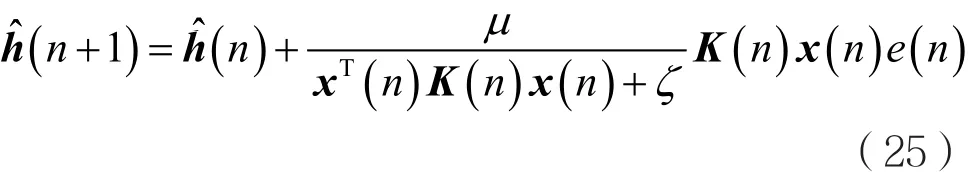
将式(25)与式(16)结合,可得MIPNSA的迭代更新方程:
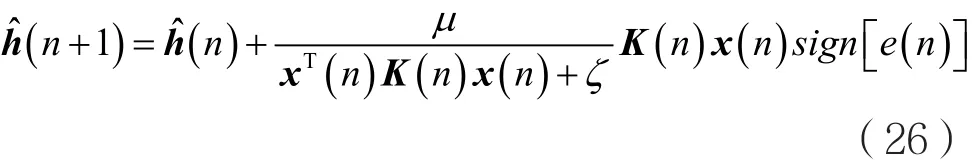
综上所述,在非高斯噪声背景下,本文提出的新算法的自适应过程可以总结如下:

3 非高斯噪声条件下的新算法
3.1 仿真条件
实验中,分别采用两种形式的输入信号进行MATLAB仿真,即随机输入信号和语音输入信号。仿真中,无记忆非线性滤波器的阶数取3,FIR滤波器的长度和线性声学回声路径的长度一致,均为128。非线性信道是由前置方程和线性声学回声路径构成。其中,无记忆非线性系数向量定义为a=[1.0,0.1,0.33]T,线性声学回声路径可以由式(32)产生[17]:
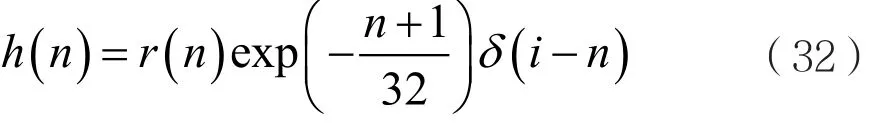
其中,n,i=0,1,…,L-1,L为脉冲响应长度,r(n)为[-0.2,0.2]的随机数,δ为Dirac函数,本文中L取128。初始化时,a^(n)与h^(n)不同,h^(n)初始化为零向量,而a^(n)初始化为a^(n)=[1,0,…,0]T。
由图3可以看出,回声路径具有稀疏性的特点,其中只有少部分的系数具有较大数值,而大部分系数的数值很小,几乎等于零。
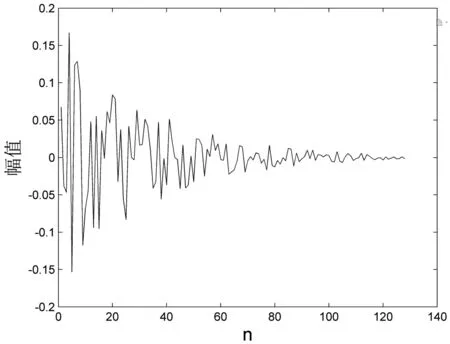
图3 声学回声路径脉冲响应h
3.2 性能指标和参数设置
实验是使算法处于等效步长[15]的条件下进行的,且以权误差向量范数(Weight Error Vector Norm,WEVN)和均方误差(Mean Square Error,MSE)的收敛曲线来评价实验结果的好坏。
非线性系数的WEVN表达式为:
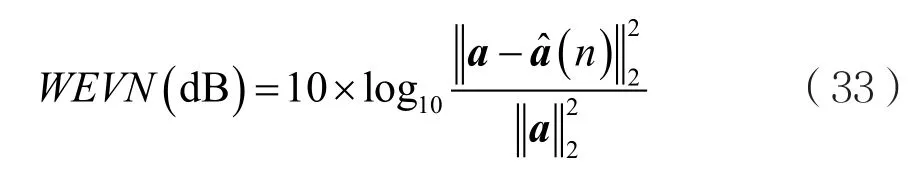
线性系数的WEVN表达式为:

WEVN的值越小,说明自适应滤波器越逼近于所跟踪的未知系统。
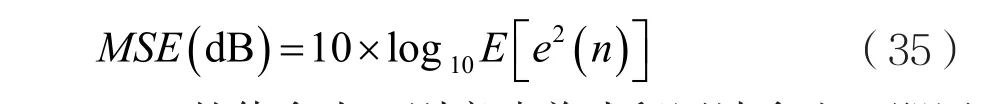
MSE的值愈小,则意味着残留回波愈少,即回声消除的效果愈好。
高斯环境下,信噪比的设置为:

非高斯环境下,广义信噪比的设置为:

其中γ为分散系数。
本文高斯条件下的信噪比设置为20 dB,非高斯条件下的信噪比同样设置为20 dB,且非高斯噪声取α=1.5条件下的α稳定分布噪声。
实验中级联方案采用的各类算法的参数设置如表1所示。

表1 级联方案采用不同迭代算法时的参数设置
3.3 仿真结果分析
本文实验是在公平原则[15]下进行的,且为了避免偶然性,每个仿真都是30次独立实验的平均结果。在以下各类算法的对比仿真图中,由于本文应用于非线性滤波器的自适应算法保持不变,只改变线性滤波器所采用的自适应算法,所以图例名称指的是应用于线性滤波器的各种算法。
3.3.1 随机信号作为输入
仿真中采用均值为零的高斯白噪声作为系统的随机输入信号。
(1)高斯噪声条件下本文方案与传统线性滤波方案的性能比较
表2中,N为二阶Volterra滤波器的线性项长度,则非线性项长度为N(N+1)/2-1,类似可推算出3阶Volterra滤波器的总长度为M=N+N(N+1)/2+N(N+1)(N+2)/6。其中,P为无记忆多项式滤波器的阶数,L为FIR滤波器的长度。

表2 两种非线性滤波器的计算复杂度
由图4和表2可以看出,本文级联方案的稳态误差值要比传统线性滤波方案大概高出10 dB。此外,与基于Volterra滤波器的方法相比,本文方法的计算量明显大幅度降低。
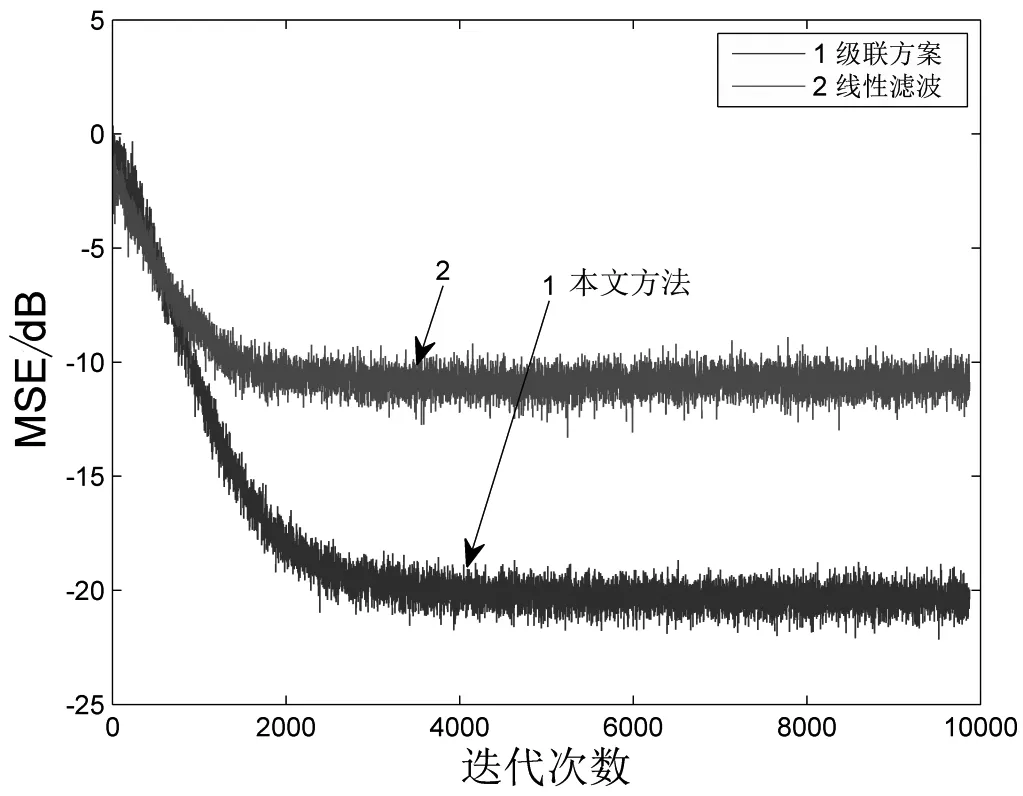
图4 两种方案在级联NLMS算法下的性能比较
(2)高斯噪声条件下各算法性能比较
图5、图6分别表示在高斯噪声条件下,线性系数和非线性系数采用以下2种方法的WEVN收敛曲线,而各算法参数设置如表1所示。
①非线性滤波器采用NSA算法,线性滤波器同样采用NSA算法,即图中1号线;
②非线性滤波器采用NSA算法,线性滤波器采用本文提出的MIPNSA算法,即图中2号线。

图5 高斯噪声条件下线性系数的收敛曲线
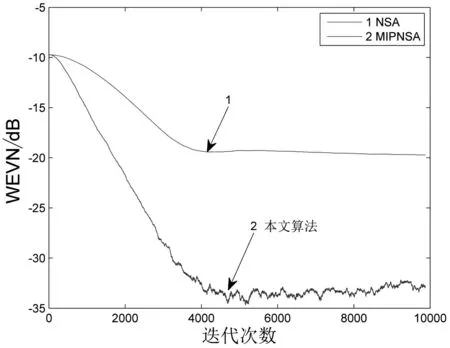
图6 高斯噪声条件下非线性系数的收敛曲线
由图5和图6可以看出,在高斯噪声背景下,虽然应用于非线性滤波器的自适应算法保持不变,但线性系数收敛性能得到改进的同时,非线性系数的收敛性能也得到了改善。同样说明,本文算法MIPNSA在高斯噪声背景下依然有效,且在收敛速度和稳态误差方面要优于传统算法NSA。
(3)非高斯噪声条件下各算法性能比较
图7、图8分别表示在非高斯噪声条件下,线性系数和非线性系数采用以下4种方法的WEVN收敛曲线,而各算法参数设置如表1所示。
①非线性滤波器采用NLMS算法,线性滤波器同样采用NLMS算法,即图中1号线;
②非线性滤波器采用NSA算法,线性滤波器同样采用NSA,即图中2号线;
③非线性滤波器采用NSA算法,线性滤波器采用IPNSA算法,即图中3号线;
④非线性滤波器采用NSA算法,线性滤波器采用本文提出的新算法MIPNSA,即图中4号线。

图7 非高斯噪声条件下线性系数的收敛曲线
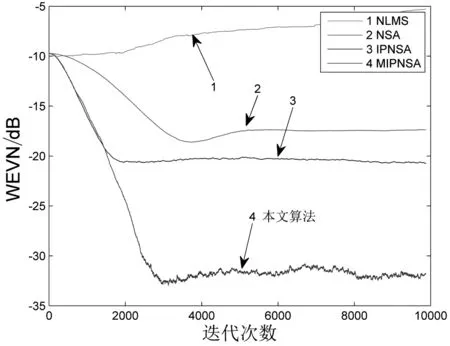
图8 非高斯噪声条件下非线性系数的收敛曲线
由图7、图8可以看出,在非高斯噪声背景下,传统的NLMS算法失效。同时,与NSA、IPNSA相比,本文MIPNSA算法性能最佳,稳态误差改善明显。
(4)各算法的计算复杂度对比
各算法的计算复杂度对比如表3所示(P表示非线性滤波器长度,L表示线性滤波器长度)由表3可得,本文改进的新算法(MIPNSA)虽然计算复杂度略微高于传统算法,但是从图5、图6、图7和图8中可以看出,其收敛速度和稳态性能都要优于传统算法。

表3 各算法的计算复杂度
3.3.2 语音信号作为输入
当系统的输入信号为真实的语音信号时,其采用采样频率为4 kHz、样本长度为20 000的非平稳语音信号,如图9所示。其他条件与高斯白噪声作为输入信号时保持一致,各算法的仿真参数设置与表1保持一致。

图9 语音信号
由图10、图11、图12、图13可以看到,不管是在高斯噪声环境下还是在非高斯噪声环境下,当输入信号为语音信号时,线性滤波器系数和非线性滤波器系数的收敛曲线能够真实反映本文提出的级联方案和本文算法MIPNSA的真实效果。虽然语音信号的非平稳特性会导致算法的收敛性能有所降低,但仿真结果仍然能够验证本文方案的可行性和有效性。

图10 高斯噪声条件下线性系数的收敛曲线

图11 高斯噪声条件下非线性系数的收敛曲线

图12 非高斯噪声条件下线性系数的收敛曲线
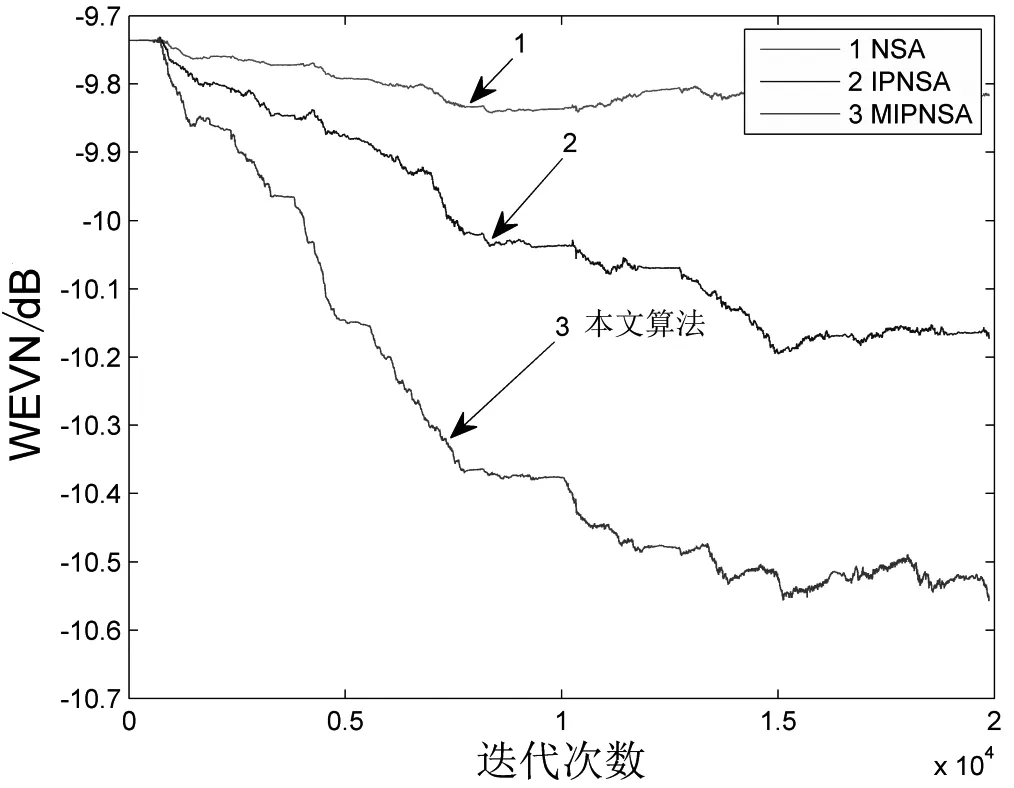
图13 非高斯噪声条件下非线性系数的收敛曲线
4 结 语
通过以上理论分析和实验仿真结果可以得出以下结论:(1)本文提出的非线性回声消除方案比线性滤波方案的回声消除效果好,其MSE对应的稳态误差值高出约10 dB,且该方案的复杂度不高,有利于工程应用的实现;(2)本文新算法MIPNSA对高斯噪声和非高斯噪声均具有良好的抑制能力;(3)通过明确系统的稀疏性与比例项权重之间的关系,新算法MIPNSA可以自动控制比例项权重并进行选值,从而进一步改善了算法性能,且相比于传统自适应滤波算法,具有更佳的收敛速度和稳态性能。
参考文献:
[1] 王正腾,谢维波.改进的NLMS算法在回声消除系统中的应用[J].计算机工程与应用,2017(10):107-111.WANG Zheng-teng,XIE Wei-bo.Application of Improved NLMS Algorithm in Echo Cancellation System[J].Computer Engineering and Applications,2017(10):107-111.
[2] 李文峰,王晓辉,孙小业等.自适应回声消除器设计[J].工矿自动化,2017(10):97-100.LI Wen-feng,WANG Xiao-hui,SUN Xiao-ye,et al.Adaptive Echo Canceller Design[J].Industrial and Mining Automation,2017(10):97-100.
[3] Rai A,Kohli A K.Volterra Filtering Scheme Using Generalized Variable Step-size NLMS Algorithm for Nonlinear Acoustic Echo Cancellation[J].Acta Acustica United with Acustica,2015,101(04):821-828.
[4] Uncini A,Nalin A,Parisi R.Acoustic Echo Cancellation in the Presence of Distorting Loudspeakers[C].Signal Processing Conference,2015:1-4.
[5] Birkett A N,Goubran R A.Limitations of Handsfree Acoustic Echo Cancellers Due to Nonlinear Loudspeaker Distortion and Enclosure Vibration Effects[C].Applications of Signal Processing to Audio and Acoustics,1995:103-106.
[6] Niemisto R,Makela T,Myllyla V.Robust Fast Affine Projection Algorithm for Nonlinear Acoustic Echo Cancellation[C].Signal Processing Conference,2012:1-4.
[7] Comminiello D,Scarpiniti M,Azpicueta-Ruiz L A,et al.Nonlinear Acoustic Echo Cancellation Based on Sparse Functional Link Representations[J].IEEE/ACM Transactions on Audio Speech & Language Processi ng,2014,22(07):1172-1183.
[8] Vaerenbergh S V,Azpicueta-Ruiz L A.Kernel-based Identification of Hammerstein Systems for Nonlinear Acoustic Echo-cancellation[C].IEEE International Conference on Acoustics,Speech and Signal Processing IEEE,2014:3739-3743.
[9] Comminiello D,Scarpiniti M,Scardapane S,et al.Improving Nonlinear Modeling Capabilities of Functional Link Adaptive Filters[J].Neural Netw,2015(69):51-59.
[10] Liu J,Liu Q,Grant S L,et al.The Block-sparse Proportionate Second-order Volterra Filtering Algorithms for Nonlinear Echo Cancellation[C].IEEE International Workshop on Acoustic Signal Enhancement,2016:1-5.
[11] Gao F X Y,Snelgrove W M.Adaptive Linearization of a Loudspeaker[C].International Conference on Acoustics,Speech,and Signal Processing IEEE,1991:3589-3592.
[12] Stenger A,Kellermann W.Adaptation of a Memoryless Preprocessor for Nonlinear Acoustic Echo Cancelling[J].Signal Processing,2000,80(09):1747-1760.
[13] XIAO L S,WU M,YANG J.A New Efficient Filtered-x Affine Projection Sign Algorithm for Active Control of Impulsive Noise[J].Signal Processing,2016,120(03):456-461.
[14] Hirano G,Shimamura T.A Modified IPNLMS Algorithm Using System Sparseness[C].International Symposium on Intelligent Signal Processing and Communications Systems IEEE,2012:876-879.
[15] 郭莹,白艳梅.稳健的仿射投影符号自适应滤波算法[J].仪器仪表学报,2017,38(01):23-32.GUO Ying,BAI Yan-mei.Robust Affine Projection Sign Adaptive Filtering Algorithm[J].Journal of Instrument and Instrument,2017,38(01):23-32.
[16] Masry E,Bullo F.Convergence Analysis of the Sign Algorithm for Adaptive Filtering[J].IEEE Transactions on Information Theory,2002,41(02):489-495.
[17] Deng H,Doroslovacki M.Proportionate Adaptive Algorithms for Network Echo Cancellation[J].IEEE Transactions on Signal Processing,2006,54(05):1794-1803.
