基于人工神经网络的水质监测模型研究
2018-05-04王雪
王 雪
(河北省唐山市水文水资源勘测局,河北,唐山,063000)
1 引言
随着国内经济的迅速发展和居民生活水平的提高,更多的工业废水和生活污水形成,由于治理措施落后和管理机制不健全,污水未经允许私自排放的现象十分严重,导致水体污染严重,河流水质急剧下降[1]。传统的水质监测方法均通过现场取样的方法进行水质指标的测定,其结果虽然较精确,但操作成本高、周期长、步骤复杂,无法实时、精确、稳定代表水域水质,且在某些条件落后地区难以实现[2]。因此,找出合理、便捷和精确的水质监测模型一直是近年研究的热点,找出合理的水质监测模型对水生态措施的制定有着十分重要的指导意义。
截止到目前,贝叶斯原理、机器学习模型、模糊评价算法等先进算法先后被应用到水质监测模型开发当中。郭小青和项新建[3]基于神经网络模型建立了水质监测及评价系统,指出了人工神经网络较强的学习、联想和容错功能,并通过实例,验证了模型的精确性;杨咪等[4]基于贝叶斯原理,在宁夏地区建立了当地水质评价模型,选取DO、CODMN等5项指标为评价因子,对模型进行了验证,模型模拟结果指出河流水质从上游到下游逐渐变差;曹宇峰等[5]将模糊数学算法引入水质评价模型中,得出的结论与实际基本一致。
然而,现如今的水质监测模型基本均集中在研究水体水质评价等级中,对某一项指标的水质监测及预测的模型研究相对较少。同时研究表明,传统的BP神经网络模型具有收敛速度较慢且易陷入极值问题导致计算错误等缺点[6]。本文将遗传算法引入BP神经网络当中,用于得出新型的水质监测模型,针对具体水质指标,选取总氮(TN)、总磷(TP)、高锰酸盐指数(CODMN)、和氨氮(NH3-N)4项指标,研究不同指标的水质监测与预测模型,并与传统BP神经网络模型预测结果对比,进一步验证该模型的优越性,得出的结论可为水资源保护政策的制定提供科学依据。
2 研究方法
2.1 遗传算法优化BP神经网络
遗传算法指的是通过模拟达尔文生物进化论的自然选择和生物进化过程的计算模型,其优点是避免局部最优解[7]。将遗传算法原理应用到BP神经网络模型中,可有效弥补BP神经网络的缺点,具体运算工程主要分为3个步骤:
首先确定神经网络计算结构,确定模型计算长度。本次水质监测模型中,神经网络计算结构指的是模型针对4种水质指标的实测数据,确定的实测数据回归变化趋势,系统自动形成回归模型结构。而模型的计算长度则为4项水质指标实测数据的个数,本文选择2008~2016年的实测数据为基础,共522组数据,选择2008~2011年的数据训练模型,即为模型计算长度;
其次每个个体通过自适应函数计算个体适应度值,找出最优解。基于遗传算法中的交叉、变异处理,优化BP神经网络的权重赋值计算,由于本文研究水质监测模型,因此每个个体指的是4项水质指标的逐次实测值模型,通过模型计算权重,与输入样本的个体适应度相乘,得出输出结果,通过公式(1)计算每个样本的个体适应度,

式中,Y代表样本的个体适应度值;a为系数;Ei和Fi分别为第i个节点的期望输出和预测输出,n为样本数量。
通过交叉、变异等处理,选择合适的个体适应度,其中每个个体的选择概率Pi可用下式计算,最终得出输出层结果:

交叉操作采用实数交叉法进行,变异操作采用变异迭代法进行,其具体计算步骤见文献[8]中的描述。
最后是神经网络预测模型的建立,通过计算每个指标样本的个体适应度,选出最优解,通过模型自动计算每个样本与实测值的误差,验证预测值是否满足要求,若满足则输出最终结果。通过上述步骤,对模拟水质变化情况,对不同水质指标进行监测,具体原理步骤见图1。本文用遗传算法优化BP神经网络(GABP)模型,预测不同水质指标变化情况,以监测水质变化。

图1 神经网络计算原理图
2.2 误差指标计算
Nash-Sutcliffe系数(CD)、逐日相对均方根误差(RMSE)和Kendall一致性系数(K)可以较好地反映长时间预测序列与实测值的误差和一致性,是系统性较好的数据评价指标体系。其中,CD与K的值越大、RMSE的值越小,模型算法与实测值的一致性越好、计算精度越高,具体公式如下:

式中:n为样本数量;A′为模型算法模拟值;Am为实测值;Am为实测值的均值;C为待检验方法与实测结果中拥有一致性元素的对数;D为待检验方法与实测结果中不具有一致性元素的对数。
3 结果与分析
3.1 不同模型水质指标精度拟合
图2为GABP模型与BP模型关于3种水质指标的模拟值与实测值的精度对比。图2显示,GABP模型对3种水质指标的模拟精度要明显高于BP模型。GABP模型模拟高锰酸盐指数(CODMN)时,与实测值的拟合方程斜率为1.060,与1十分接近,这表明模拟值与实测值的误差较小,同时其决定系数R2为0.727,且相关性达到了极显著水平(P<0.01),而BP神经网络模型模拟值斜率为1.77,决定系数R2仅为0.298,表明模拟值的误差较大,且BP神经网络模型普遍高估了CODMN的值;GABP模型模拟总氮(TN)时,与实测值的拟合方程斜率为0.950,与1十分接近,这表明模拟值与实测值的误差较小,同时其决定系数R2为0.864,且相关性达到了极显著水平(P<0.01),而BP神经网络模型模拟值斜率为1.59,决定系数R2仅为0.498,表明模拟值的误差较大,且BP神经网络模型普遍高估了TN的值;在模拟总磷(TP)时,其结论基本一致。这表明GABP模型在水质模拟中的计算精度普遍较高。
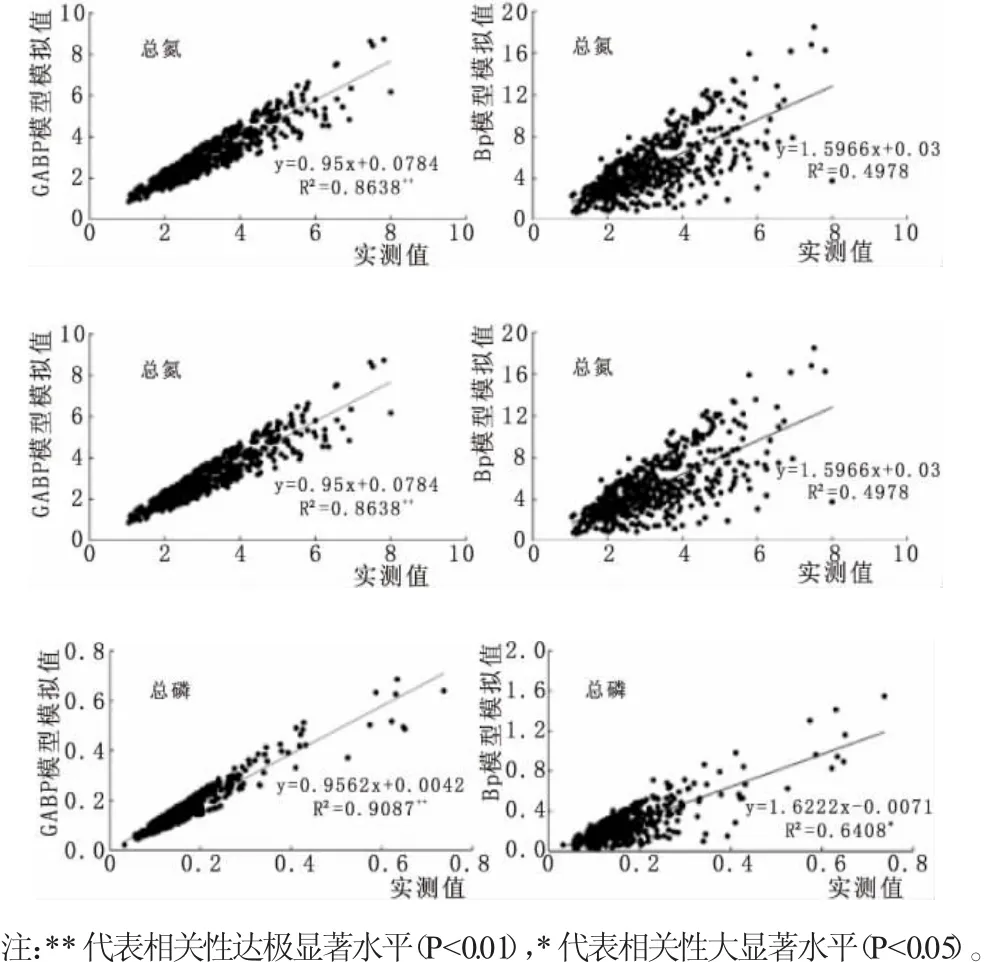
图2 不同模型不同水质指标模拟精度对比
3.2 不同模型水质指标精度指标体系对比
表1为不同模型计算结果与实测值的计算精度指标分析。表1显示,不同指标GABP模型模拟结果的计算误差均较低,且结果与实测值的一致性均较高。在计算CODMN时,GABP模型计算结果的RMSE仅为0.301,CD和K值分别达到了0.874和0.921,且相关性均达到了极显著水平(P<0.01),而BP模型RMSE达到了0.654,CD和K值分别仅为0.301和0.432,且相关性均未达显著水平(P>0.05);在计算TN时,GABP模型计算结果的 RMSE仅为 0.257,CD和 K值分别达到了 0.864和0.798,且相关性均达到了极显著水平(P<0.01),而BP模型RMSE达到了0.723,CD和K值分别仅为0.412和0.298,且相关性均未达显著水平(P>0.05);在计算TP时,结论与其余2个指标基本一致。综上所述,GABP模型模拟值与实测值相比,计算误差较小,计算结果一致性较高,模型模拟精度较高。

表1 不同模型不同水质指标模拟精度指标体系计算结果对比
4 结论
本文用遗传算法优化BP神经网络模型,以3种水质指标实测值为基础,以期模拟水质指标,得出用于水质监测的模型,将得出的结果与BP神经网络模型做了对比,指出GABP模型在模拟3种水质指标时,与实测值的拟合方程斜率均接近于1,决定系数R2均在0.70以上,CD和K值也均超过了0.85,且相关性达到了极显著水平,表明该模型用于模拟水质指标的精度较高,但由于本研究仅选取了3种水质指标进行验证,对其余指标的验证应在今后的研究中进一步讨论。
[1]刘国东,黄川友,丁晶.水质综合评价的人工神经网络模型[J].中国环境科学,1998,18(6):514—517.
[2]张春桂,曾银东,马治国.基于模糊评价的福建沿海水质卫星遥感监测模型[J].应用气象学报,2016,27(1):112—122.
[3]郭小青,项新建.基于神经网络模型的水质监测与评价系统[J].重庆环境科学,2003,25(5):8—10+25.
[4]杨咪,屈文岗,钱会.基于熵权的贝叶斯模型及其在水质评价中的应用[J].灌溉排水学报,2018,37(1):1—7.
[5]曹宇峰,林春梅,孙霞.模糊数学法在海洋水质评价中的应用[J].海洋技术,2011,30(2):118—122.
[6]李松,罗勇,张铭锐.遗传算法优化BP神经网络的混沌时间序列预测[J].计算机工程与应用,2011,49(29):52—55.
[7]刘振华,赵英时.基于遗传算法的不同光照条件下植被和土壤组分温度反演[J].农业工程学报,2012,28(1):161—166.
[8]仲云飞,梅一韬,吴邦彬,等.遗传算法优化BP神经网络在大坝扬压力预测中的应用[J].水电能源科学,2012,30(6):98—101.
