间歇过程的灰色迭代学习控制
2018-05-04吴晓威杨会敏
吴晓威, 赵 芳, 连 蓉, 杨会敏
(中车永济电机有限公司研发中心, 陕西 西安 710018)
引言
在间歇过程中,安全性、稳定性和高质量的产品是对生产所提出的最基本的目标。由于存在着模型不确定性、时变、非线性、反应机理复杂等特点,要求控制器不仅能有效克服纯滞后而且具有抗强干扰的能力还要对时变特性的适应能力和对非线性现象的控制能力,只有这样才能保证间歇过程控制系统的动态稳定性和稳态精度。文献【1】指出,对于间歇过程,迭代学习控制是一种有效的先进控制方法。文献[2]提出一种反馈—前馈迭代学习算法,该方法在开环迭代学习控制系统中引入反馈环,利用迭代偏差当前时刻的历史数据更新对象当前前馈输入。然而,实际的间歇过程控制系统或多或少的存在滞后和干扰,只采用迭代偏差的历史数据更新对象当前前馈输入的算法,导致迭代偏差较大,会破坏控制的鲁棒性,使得被控参数波动较大,有时甚至会使系统失去稳定性。
为了解决迭代学习算法收敛性的问题,本文提出一种新的基于灰色预测的迭代学习算法,在原有的反馈—前馈迭代学习算法的基础上,引入灰色预测的思想,用预测迭代偏差代替当前输出与期望的偏差。用灰色系统模型GM(1,2)预测系统输出,从而求出预测偏差。
1 基于灰色预测的迭代学习控制算法
基于灰色预测的迭代学习控制器,采用简单的PID型控制,对实时过程进行控制;采用迭代学习的方法偏差消除级,同时为了保证迭代学习的收敛性,反馈—前馈迭代学习算法中采用灰色预测得到预测偏差,如图1所示。
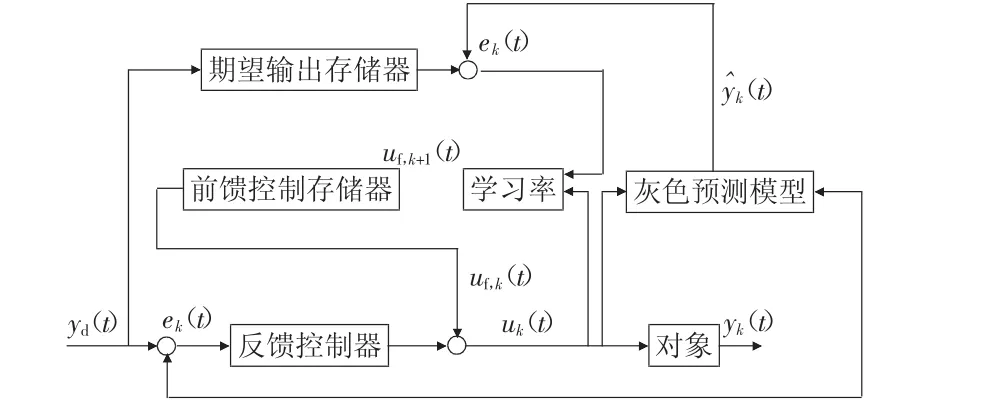
图1 基于灰色预测的迭代学习控制结构图
1.1 灰色预测模型
文献【3】讲述了灰色系统模型 GM(1,2)建模方法以及该建模方法的优点。
设可测得其输入和输出时间序列如下:
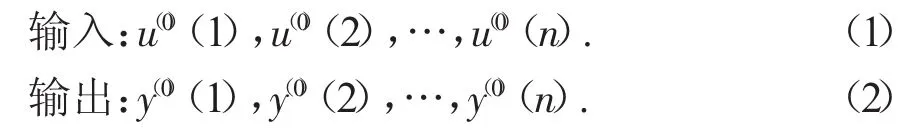
对该序列(1)和(2)进行一次累加生成1-AGO得:
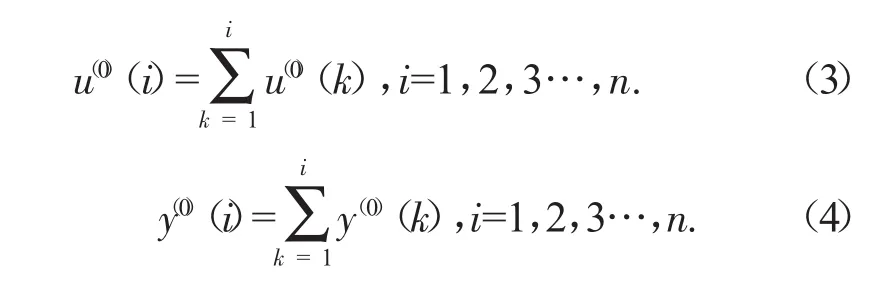
利用一次累加生成数据列(3)和(4),可建立GM(1,2)微分方程:
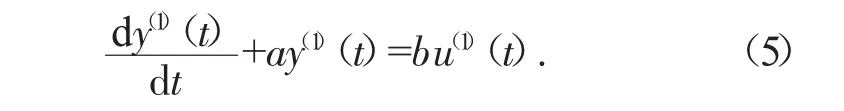
其中,系数a和b有下式估计:
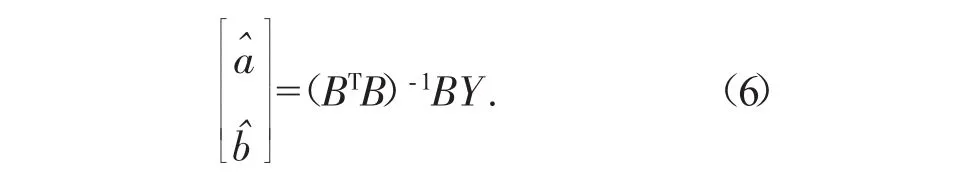
其中:
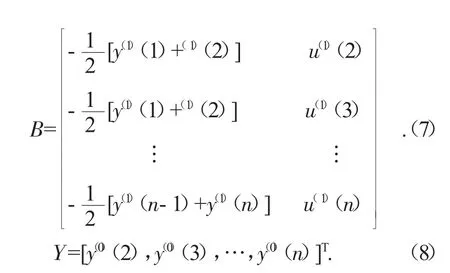
将式(5)其离散化得到:

式中:T为采样周期。
将式(5)乘以差分算子的平方Δ=1-z-1(z-1为滞后算子),经整理得:
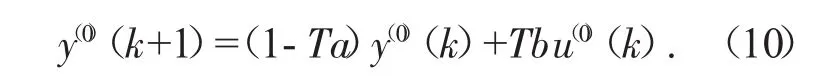
将式(10)化简为:
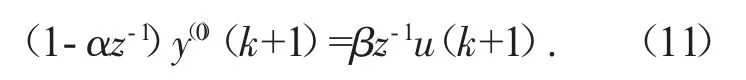
式中:α=1-Ta,β=Tb。
系统估计模型传递函数为:

1.2 基于灰色预测的迭代学习算法
文献【4】采用迭代前馈和PID反馈相结合的迭代学习控制算法,
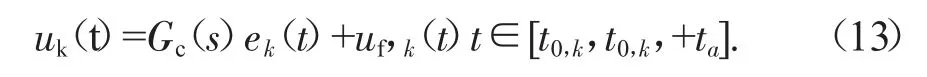
式中:t0,k为第k次循环的初始时间;ta为运行时间,为当前的迭代输入值;为反馈项,
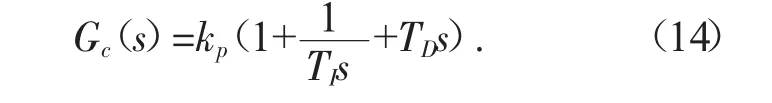
Uf为迭代的前馈项,
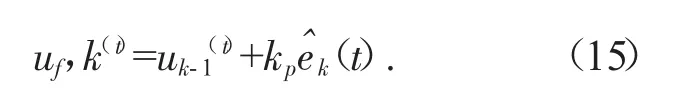
其中kp为学习增益矩阵。
为了保证迭代学习的收敛性,在当前控制输入中引入未来时刻的迭代偏差,该偏差是未来时刻的预测输出与给定的期望输出之差。
2 收敛性研究
对于系统Y=GU,采用本文方法描述的迭代学习控制算法。若满足
3)过程零输入响应是不变的,即 y(0)(s)则当 k→∞时,系统迭代输出yk(t),收敛于期望轨迹yd(t)。
则由式(14)和(15)得到:
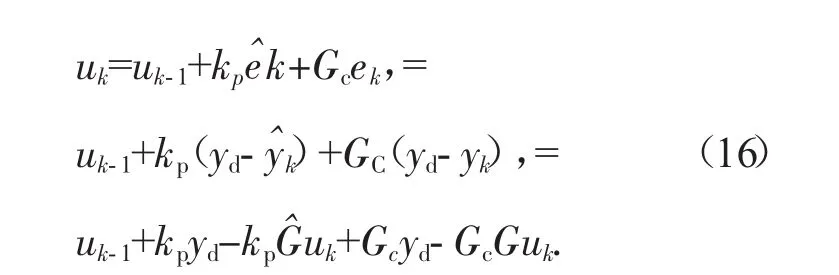
由式(16)得到:
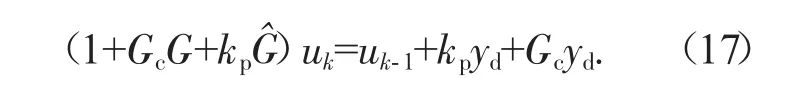
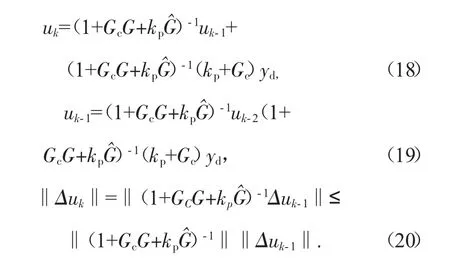

由此可见,基于灰色预测的迭代学习算法是收敛的。
又由于
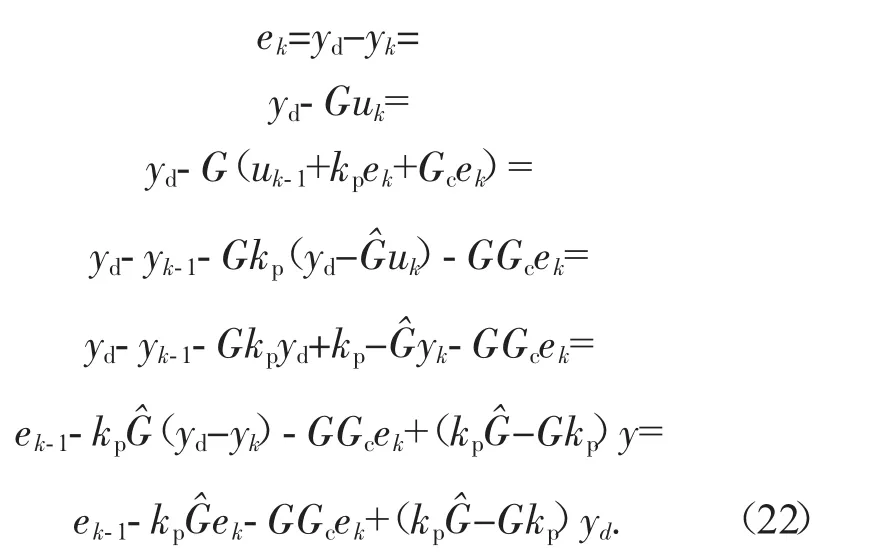
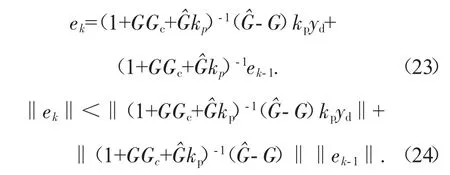
3 鲁棒稳定性研究
若yd(s)-y0(s)∈H2,E(s)∈H2并满足估计模型与实际模型完全匹配G=G^,换句话说
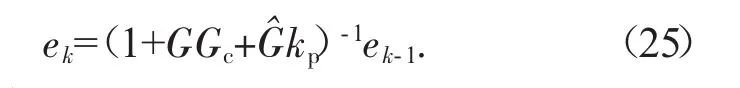
由式(25)得:
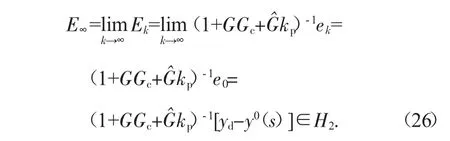
由式(25)和式(26)得
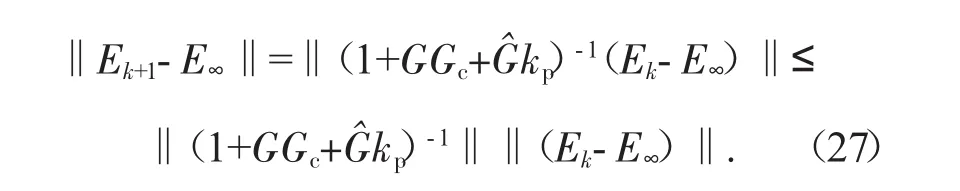
由此可以证明系统具有鲁棒稳定性。
4 仿真研究
4.1 系统辨识
采用等维新息滚动的灰色预测模型GM(1,2),建模维数选为5。图2中给定输入信号为。从图3可以看出,等维新息滚动的灰色预测模型GM(1,2)得到的系统输出与实际非线性系统输出非常接近,辨识误差非常小。利用公式求出总平均残差为 0.004 8,预测精度由(1-e(avg))×100%得为99.52%。图4为参数a与b的变化曲线图。由此可知,系统的估计模型与实际系统几乎完全匹配,满足系统稳定的前提假设。
4.2 输出跟踪研究
给定参考输入 r(k)=sin(2×pi×k/50),在仿真中,比例系数kp=0.2;积分时间常数Ti=1;微分时间常数Td=0.5。迭代学习算法中,kp的作用是减少预测偏差和加快响应速度。通过多次试验研究及分析,建立kp的变化规律为
采用自适应调整kp参数,明显优于固定kp的学习效果。从图5可以看出,随着分批数k增加,跟踪效果明显变好。图6为各批次输出误差曲线。图7为以过程输出变量的泛化均方根误差:RMSEk=为标准的各批次跟踪情况。从图6可以看出,随着批次数的增加,输出误差的RMSE值总体趋势是逐渐减少。

图2 灰色系统辨识图

图3 预测输出与实际输出比较图以及辨识误差
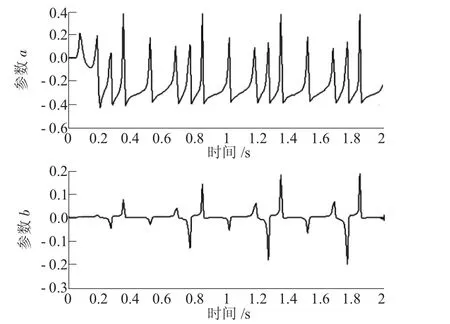
图4 参数a与b的变化曲线图
5.3 鲁棒性分析
用灰色预测迭代学习算法控制不确定系统G=G(0s)(1+0.8W2)(s),其 中 ,

图5 各批次输出跟踪曲线

图6 各批次输出误差曲线
图8为各批次输出跟踪曲线。图9为各批次输出误差曲线。图10为各批次均方根误差(RMSE)跟踪性能曲线。从图8可以看出,灰色预测迭代学习算法对于不确定系统具有良好的鲁棒性。
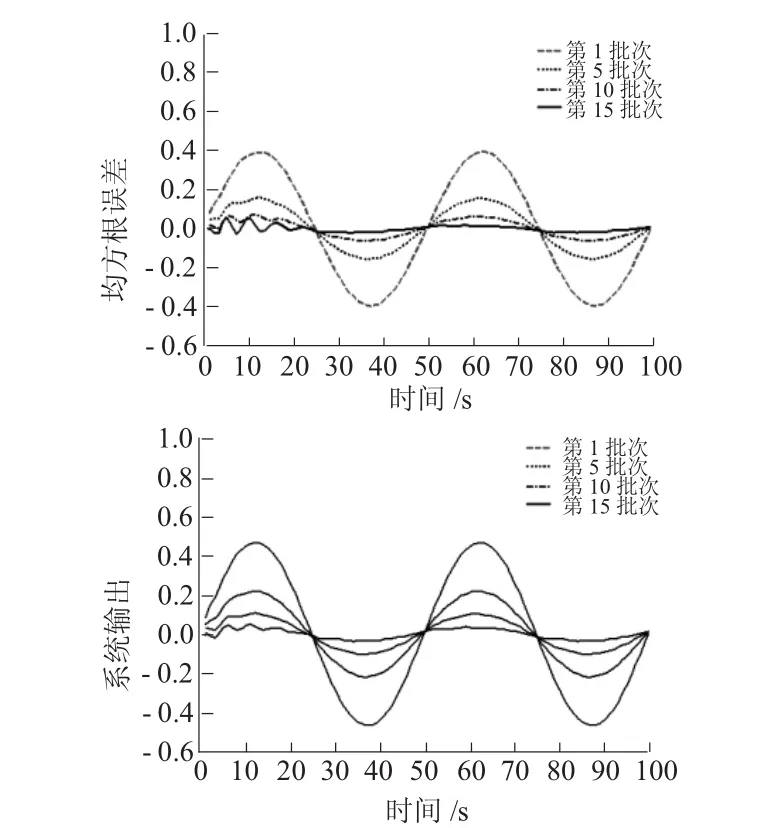
图8 各批次输出跟踪曲线
5 结论
图9 各批次输出误差曲线
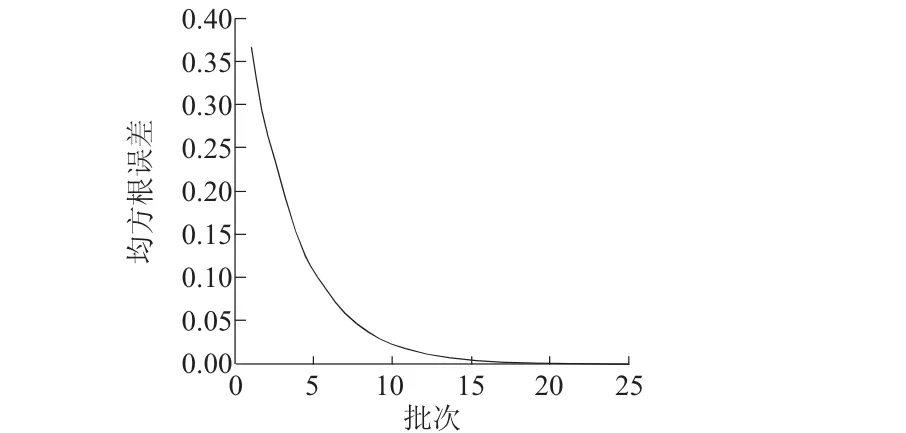
图10 各批次的均方根误差(RMSE)跟踪性能
针对不确定间歇过程,提出了一种新的基于灰色预测的迭代学习控制器设计方案。该方法将灰色预测与迭代学习算法结合,不仅改善了迭代学习控制系统的稳定性,同时克服工业生产中的不确定因素产生的影响。理论分析和仿真试验结果表明,该控制策略具有收敛性和鲁棒稳定性,对不确定间歇过程能实现有效控制。
[1]Lee J H,Lee K S.Iterative learning control applied to batch processes:An overview[J].Control Engineering Practice,2007,15(10):1 306-1 318.
[2]Kuc T Y,Jin S L,Nam K.An iterative learning control theory for a class of nonlinear dynamic systems[J].Automatica,1992,28(6):1 215-1 221.
[3]邓聚龙.灰色控制系统[M].武汉:华中理工大学出版社,1993.
[4]谢胜利.迭代学习控制的理论与应用[M].北京:科学出版社,2005.
[5]Doh T Y,Chung M J.Robust ILC with Current Feedback for Uncertain Linear Systems[C]//Iterative learning control.1998:193-208.
