基于改进消失矩复小波的输电线路故障测距*

汪 梅， 徐长丰， 王伟峰， 赵春婷

(1．西安科技大学电气与控制工程学院 西安，710054) (2．西安科技大学陕西省煤火灾害防治重点实验室 西安，710054) (3．西安西电光电缆有限责任公司电缆研究中心 西安，710086)

引 言

输电线路是电网重要的组成部分，其稳定可靠的运行对整个电网的安全运行有重要的意义。输电线路发生故障时会在线路中产生故障行波，其中包含电流行波和电压行波。行波中包含丰富的故障信息，若及时准确地找到故障的位置并予以切除，将行波中的故障信息识别出来，对恢复供电，减少国民经济损失有不可估量的作用[1]。

已有大量国内外学者将小波理论应用于输电线路故障测距。文献[2]根据配网线路故障行波特性构建一种故障匹配的母小波，构建出的小波与故障行波匹配度高，但存在一定程度的频带混叠，致使故障波头识别有很大的误差。文献[3-4]利用db小波分析线路故障信号，将模极大值算法与相关技术、支持向量机(support vector machine，简称SVM)结合起来，使奇异点检测效果优于单一的小波变换，但对于含有高频噪声的信号，模极大值提取故障信息还是不够准确。文献[5]采用小波包节点系数优化技术处理电缆线路匹配波形，修正了由于传播衰减引起的入射波与反射波波形失真，保证波形相关性匹配的准确性，但忽略了故障反射波的复杂性。鉴于实小波分析故障信号的局限性，这也为复小波应用于输电线路故障测距提供了契机。文献[6]构造的时域紧支复小波相频特性变化灵活，易与被分析信号匹配。文献[7]通过分析复小波相频特性，提出复小波变换的复合信息，其对于信号细微变化的检测将更具优势。文献[8]构造出一种双树复小波，在保留实小波优点的情况下克服了实小波频域混叠、缺乏相位信息以及系数震荡等缺点，这对高频故障信号的分析是很重要的，特别是输电线路中的故障行波。由于输电线路故障行波是暂态的、突变的高频信号，其故障信息复杂同时难以分析，利用复小波分析故障信号，可以结合幅频和相位信息，有着实小波所不可比拟的优势[9]。因此，对复小波的研究也是迫切必要的，对其进行参数优化以及结构调整将更有利于故障信号中故障信息的提取。

基于上述研究现状和不足，笔者提出利用改进消失矩的高斯复小波分析故障信号，从小波消失矩和故障信号奇异性出发，分析消失矩对奇异性的影响，提出基于故障奇异性的消失矩改进判据，在判据的基础上，对输电线路故障行波进行复小波分解，进而计算邻幅比和相位畸变率以进一步优化小波消失矩，选取最优消失矩的高斯复小波。

1 故障测距总体方案

笔者将高斯复小波应用于输电线路故障测距，从小波消失矩的角度出发分析消失矩与信号奇异性的关系，探讨如何选择合适消失矩的高斯复小波来分析故障信号，考虑到故障行波的复杂性，从而更进一步地分析不同消失矩高斯复小波对故障行波敏感性问题，并利用邻幅比和相位畸变率对消失矩进行优化。继消失矩讨论之后，对输电线路中故障行波产生过程进行分析，并对测距方法进行讨论。在仿真和实验中，将幅频和相位信息结合来提取故障时间，并进行故障测距。总体方案如图1所示。

图1 故障测距方案示意图Fig.1 Schematic diagram of fault location

2 小波消失矩及其改进机理

由于故障信号奇异性的差别，这对小波消失矩提出了不同的要求，为了有效地将信号中的奇异性检测出来，复小波就应该具有一定阶数的消失矩。

2.1 小波消失矩

消失矩是衡量小波特性的重要参数，可描述为

(1)

其中：ψ(x)为小波函数，则称小波ψ(x)具有0-(N-1)阶消失矩；n为消失矩的阶数。

在分析故障信号时，不同的信号奇异性对消失矩有不同的要求[10]。由傅里叶的矩量定理可得

(2)

其中：ω为角频率。

因此ψ(ω)具有n个消失矩时

ψ(n-1)(ω)ω=0=0

(3)

通过式(2,3)可以说明，小波的消失矩越高，小波的频谱低端的衰减速度越快，对应的小波变换越容易滤除掉信号中变化缓慢的部分(即低频部分)，从而可以突出信号中的奇异部分。

为了更直观地描述消失矩阶数对复小波时频域的影响，现以高斯复小波族为例，分别取消失矩阶数为n=1和n=10高斯复小波以进行对比，如图2所示。由图可知，在时域上，消失矩越大，小波函数幅值振荡越剧烈，时域宽度变窄，幅值变小；而在频域上，消失矩越大，波动变缓，幅值变大，频宽增大。

图2 两种消失矩时频幅频比较示意图Fig.2 Comparison in two types of vanishing moment

2.2 信号奇异性分析

信号的奇异性通常利用Lipschitz指数来表征信号的奇异性[11]，即为Lipschitzα。信号的奇异性大致可分为两种：一种是信号在某一时刻发生突变，引起的信号不连续；另一种是外观很光滑，但是信号在某处的微分不连续。

现用Lipschitzα描述故障信号的奇异性。若n为一非负整数，n<α≤n+1，且存在两个常数A，h0>0及n次多项式Pn(h)，使得对任意的常数h≤h0均有

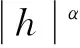
(4)

则称f(x)在点x0为Lipschitzα。如果式(4)对所有x0∈(a,b)时均是成立的，且x0+h∈(a,b)，则称f(x)在(a,b)上是一致Lipschitzα。当f(x)在x0处连续可微，则其Lipschitz指数为1；当f(x)在x0是奇异的，则其Lipschitz指数小于1；当f(x)在x0处不连续但有界，则其Lipschitz指数为0。

2.3 消失矩改进机理

为了揭示小波消失矩与信号奇异性的联系，这里先给出衰减性的定义[12]。设具有n阶消失矩的小波ψ(t)，其导数是快速衰减的，即对任意正整数p和m，其中0≤p≤n，m∈N，存在常数Cm，使得

(5)

其中：t为信号时间变量；R为实数集。

设快速衰减的小波具有n阶消失矩，当且仅当存在快速衰减函数θ(t)使得

(6)

成立时，信号f的小波变换为

(7)

其中：s为尺度因子；k为平移因子。

当且仅当对θ(t)的积分不为零时，此时ψ(t)具有不超过n阶消失矩。从式(6，7)可知，具有n阶消失矩的小波，其小波变换可利用一个n阶的多尺度微分算子来代替。

在衰减性的理论上，讨论如何利用Lipschitz指数确定小波消失矩阶数。设n为正整数且α≤n，f(x)∈L2(R)，L2(R)为二阶可导连续区间，在点x0处是一致Lipschitzα，则存在常数A>0,使得对于x0的一个领域内的所有点x和任意尺度s>0，有

(8)

反之，设f(x)是有界函数，且当α≤n时，f(x)在点x0处是一致Lipschitzα，若存在ε>0和常数A，B>0,则对于x0的一个临域内的所有点x和任意尺度s，有

|Wψf(s,k)|≤Asε

(9)

(10)

由式(8～10)可知，3个式子在α≤n条件下成立，也就是在α≤n时小波变换的结果都是小于在某一尺度下的常数。因此，在Lipschitzα>n时，小波变换结果处于发散状态，小波变换不能给出Lipschitz指数的任何信息，无法达到检测信号奇异性的目的[13]。

通过以上论述可知，消失矩阶数n必须要大于Lipschitz指数，而不可随意的选取。结合在2.2节中对消失矩的讨论，选取消失矩时其阶数应尽量大，较大的消失矩可以使小波变换域的能量更为集中，从而压制同一尺度上变化缓慢部分对应的小波系数值，有利于突出信号中的奇异部分，以取得更好的故障分析效果。但消失矩的阶数也是有限的，随着消失矩阶数的增大，小波分析的复杂程度会越来越大，计算速度会越来越缓慢[14]。

3 消失矩阶数的优化与选取

现以短路故障为例，利用不同消失矩高斯复小波对故障信号进行变换，通过消失矩对故障识别准确度来选择最优消失矩阶数。首先定义文中所使用的两个名词：邻幅比和相位畸变率。在经复小波变换后的幅频特性的峰值中幅值最大值与次于幅值最大值之值的比值即为邻幅比，其表达式为

RM=M1/M2

(11)

其中：RM为邻幅比；M1为峰值中幅值最大值；M2为峰值中次幅值最大值之值。

对于相位畸变率，在经复小波变换后的相位信息中相位畸变部分占整个相位的比率即为相位畸变率，其表达式为

RP=t1/t2

(12)

其中：RP为相位畸变率；t1为相位畸变时间；t2为相位总时间。

对邻幅比中的幅值和相位畸变率的相位畸变时间选取(电压信号)如图3所示，幅频特性中的幅值最大值和次幅值最大值之值都已标识出，在相位信息中，畸变时间t1和t2的和也即是总畸变时间。对故障信号分析过程中，邻幅比体现了相应消失矩对干扰信号的抑制作用以及突出奇异性的效果，相位畸变率体现了变换结果的稳定程度，邻幅比越大，相位畸变率越小，对应阶数的消失矩对奇异点越敏感，复小波对故障信息的提取就越准确。

图3 幅值和相位畸变时间选取示意图Fig.3 Choose modulus and phase distortion time

现选取在不同故障类型下A相故障电压波形，利用不同消失矩的高斯复小波对故障信号进行变换，对应的邻幅比和相位畸变率如表1和表2所示。从表1和表2中可看出，随着消失矩阶数的增加，邻幅比和相位畸变率并没有呈现出线性增加的态势，邻幅比先是随着消失矩的增加而增加，当消失矩阶数到达4阶时，邻幅比达到最大；相位畸变率随着消失矩的阶数增加而平缓的增加，在4阶消失矩时，其值接近于最小。

表1 故障信号邻幅比

表2故障信号相位畸变率

Tab.2Phasedistortedrateoffaultsignal

%

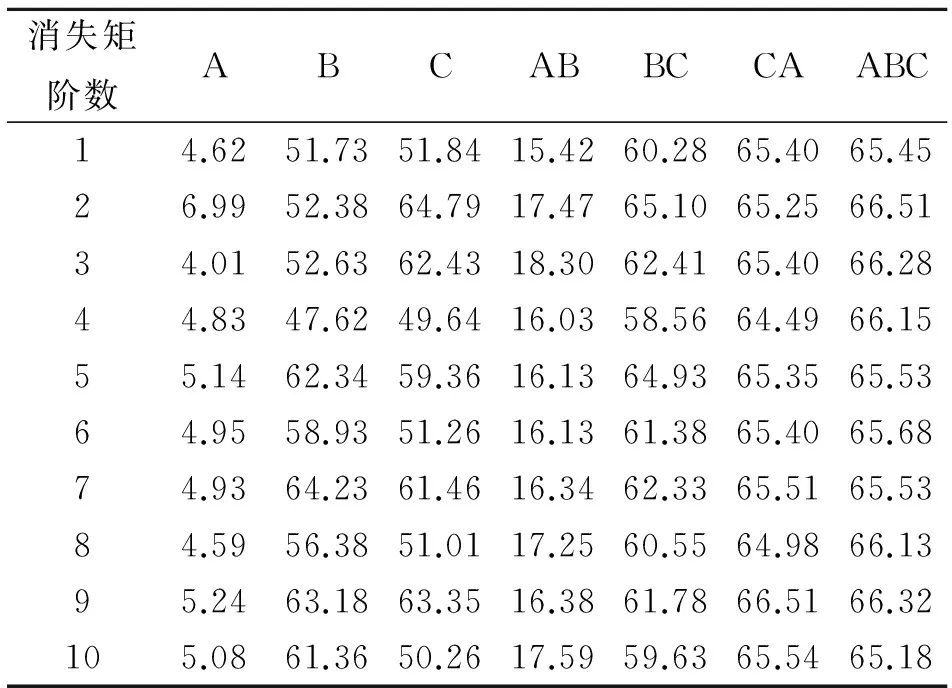
在图4，图5中，幅频特性和相位信息中的故障点和干扰都已标出。可以看到随着消失矩的增大，幅频信息中的峰值会迅速的减小，相位畸变率会逐渐变大，这样的变化对故障点的检测是不利的。由于在选取消失矩阶数时，应本着邻幅比越大相位畸变率越小的原则，因此文中用于故障检测的最优高斯复小波消失矩的阶数是4阶，4阶消失矩的高斯复小波不仅可以很好地抑制干扰信息，使其减少17.84%，而且能最大限度地减小相位畸变率，使相位畸变率减小4.12%，在分析故障时使故障特征更加的清晰。

图4 消失矩n=4和n=9时幅频特性与相位信息Fig.4 Magnitude frequency and phase information when vanishing moment n=4 and n=9

图5 消失矩n=5和n=10时幅频特性与相位信息的示意图Fig.5 Magnitude frequency and phase information when vanishing moment n=5 and n=10

4 基于故障行波传播特性的测距方法

输电线路发生故障时，在故障点会产生向线路两端传播的行波[15]。如图6所示，图6(a)是一个输电线路模型，当f点发生故障时，根据叠加原理，故障点的电压可以分解为故障前的稳态电压uf1和故障电压uf2之和。在uf2电压作用下，故障网络中将会出现故障电流和电压，并产生向线路两端传播的暂态行波，如图6(d)所示。

图6 利用叠加原理分析故障行波示意图Fig.6 Schematic diagram of analyze fault traveling wave by superposition principle

若将单根无损分布参数线路的电压u和电流i用在线路上的位置x和时间t的偏微分方程来表示

-∂u/∂x=L∂i/∂t

(13)

-∂i/∂x=C∂u/∂t

(14)

其中：L，C为线路单位长度的电感和对地电容。

将其分别对x，t微分，经变换可得到波动方程

(15)

(16)

波动方程中电压和电流的达朗贝尔解为

(17)

(18)

其中：u1为沿x正方向传播的前行波；u2为沿x反方向传播的反行波；v行波的速度；Zc为波阻抗。

文中采用的是单端行波测距法，它利用在线路一端测量到的故障暂态行波在故障点与本端或者对端母线之间往返一次的传播时间计算故障点到本端或者对端母线之间的距离。单端行波测距的示意图如图7所示，故障行波第1次到达m端的时间为t1，第2次到达m端的时间为t2，故障距离为Lx，设行波的传播速度为v，则行波测距的公式为

Lx=(t2-t1)v/2

(19)

图7 单端距法示意图Fig.7 Schematic diagram of single-ended fault location

5 仿真分析与实验验证

5.1 故障测距仿真

仿真对象是一个220 kV双端输电系统，仿真模型利用Matlab工具中的Simpower System建立，线路全长200 km，如图8所示，系统中的线路参数为：R1=0.021 Ω/km，R0=0.11 Ω/km，L1=0.89×10-3H/km，L0=2.29×10-3H/km，C1=12.94×10-9F/km，C0=5.23×10-9F/km。分别在线路的50，100和150 km处设置故障。

图8 故障仿真模型示意图Fig.8 Schematic diagram of model of system in fault

现以故障发生在距离测量端50 km处A相短路为例，故障的行波波形如图9所示，其正向行波经4阶消失矩的高斯复小波变换后的幅频特性和相位信息如图10所示。图9中对于正向行波，其在传播过程中受到的扰动比较大，没有呈现出规律性传播。经过4阶高斯复小波变换后，在图10中可以看到，幅频特性中干扰信号明显得到了抑制，而行波中的奇异点得到了突出，也即是模极大值；在图10的相位信息中，相位畸变剧烈的地方也即是行波故障点的位置。因此，当故障行波中干扰过强时，可以先通过相位信息中相位的畸变情况来判断行波中故障点的大概位置，再利用幅频特性中与相位畸变剧烈所对应的幅频峰值来确定故障行波反射的准确时间。

图9 50 km故障处的正向行波和反向行波示意图Fig.9 Schematic diagram of forward traveling wave and back traveling wave in 50 km

图10 经复小波变换后的正向行波幅频特性和相位信息Fig.10 Magnitude frequency and phase information for forward traveling wave

考虑到行波在传播过程中的能量衰减，本次实验中只取了行波前4次的反射波峰，幅频特性的峰值与其所对应相位畸变剧烈的地方都已用箭头标出。幅频特性中前4个峰值之间的平均间隔为34.04，单位间隔的时间为10-5s，得到行波在故障点和测量点之间传播的时间差Δt=17.02×10-5s，代入测距公式(19)则得到故障距离为49.91 km，其误差为0.18%，其误差在允许的范围之内。表3为4阶消失矩高斯复小波的测距结果，表4为10阶消失矩高斯复小波的测距结果，表5为db4实小波的测距结果。

从表3可以看出，在4阶消失矩高斯复小波分析的结果中，不同故障点的测距结果也是不同的，但其测距误差总体上都控制在0.76%左右。表4中10阶消失矩高斯复小波分析结果都在6.82%左右，比4阶消失矩分析结果高了6.06%；在表5中，db4实小波分析结果都在5.61%左右，比4阶消失矩分析结果提高了5.82%。

表3 4阶消失矩高斯复小波测距结果

表4 10阶消失矩高斯复小波测距结果

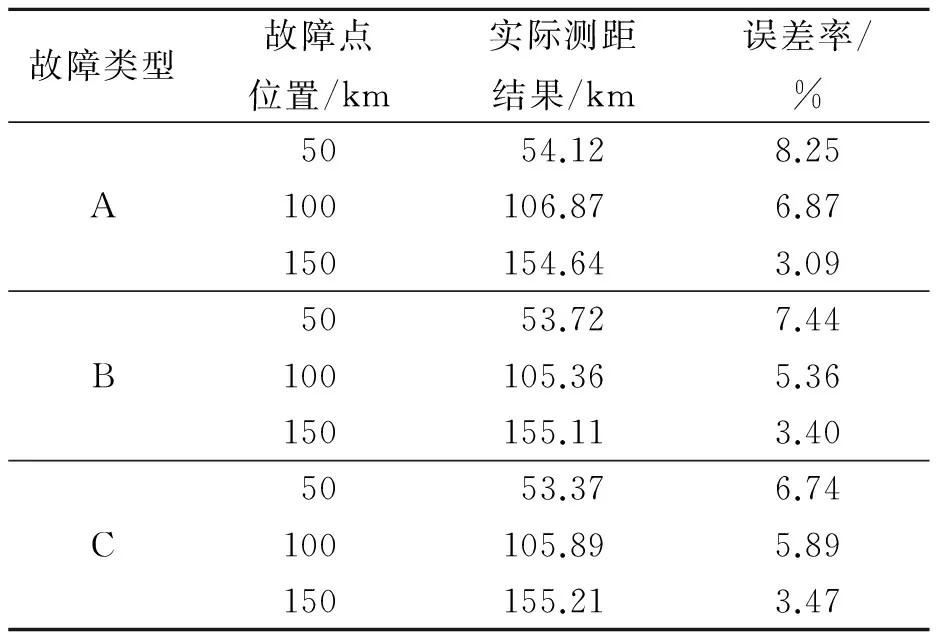
表5 db4实小波测距结果

由3个表中的数据可知，最优消失矩的高斯复小波能更准确地测出故障距离，其精度比一般的消失矩高斯复小波和实小波要高出5%左右。由于在实际电网中存在着诸多干扰因素，其测距的误差也可能会有所改变，在本次仿真中已将一部分干扰考虑在内，力求测距结果可以在一定的可控范围之内。

5.2 实验验证

实验系统在380 V矿井模拟输电线路系统上进行，其实物图如图11所示。

图11 矿用供电线路故障诊断系统Fig.11 Experimental system in coal mine

线路对地电容、电感、电阻分别为C1=0.22×10-6F，L1=6.36×10-3H，R1=2 Ω。分别进行AB相间短路和C相单相短路实验。现取500 m处AB相间短路故障电压行波信号，分别利用Cgau4，Cgau10和db4这3种小波对行波信号进行处理，为了便于比较3种小波变换后的结果，将三者幅频特性集于图12中。

图12 三种幅频特性比较Fig.12 Comparison of three types magnitude-frequency

由图12可知，经Cgau4处理后，其幅频特性在量级上要远大于Cgau10和db4的处理结果，Cgau4的幅频特性中模极大值都是以单一孤立波峰的形式存在，没有频谱混叠的现象，故障点清晰明确，易于读取故障时间；Cgau10的幅频特性中受到干扰比较严重，随着行波能量的衰减，模极大值逐渐被干扰所掩盖，以至于后续反射的波形中故障点已经无法辨识；db4的幅频特性中，故障点波形比较混乱，没有单一的波峰峰值点，同时其幅频特性在量级上有显著减小，这些都给故障点的判断带来了较大的难度。可见，普通消失矩的复小波和实小波对实际故障线路波形的分析效果远不如最优消失矩复小波的分析效果，改进消失矩的高斯复小波的有效性和优越性也是显而易见的。

现利用Cgau4对不同故障距离下AB相间短路和C相单相短路的行波进行分析，实验结果如表6所示。考虑到实验线路较短，设备采样频率有限，而致使本次实验误差率要大于仿真误差率。就总体而言，误差率是符合要求的。

6 结束语

笔者提出利用改进消失矩的高斯复小波处理输电线路故障信号。讨论了消失矩与信号奇异性的关系，分析了消失矩对故障测距的影响，以及如何选取

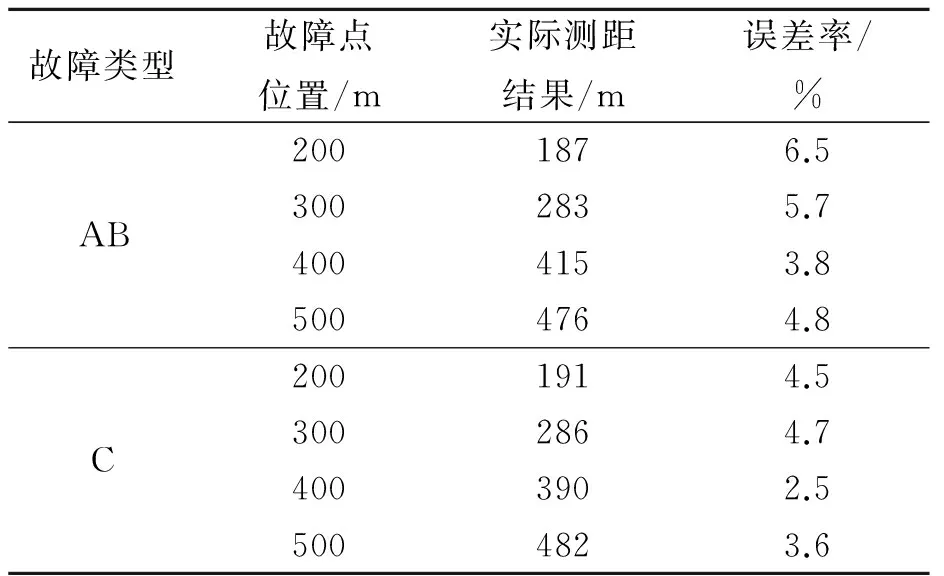
表6 矿用供电线路实验结果

最优消失矩的复小波提取故障信息。通过全文论述可以得出以下结论：

1) 消失矩是小波的一个重要的参数，当Lipschitz指数小于小波消失矩的阶数时，小波变换无法有效检测出信号的奇异性，因此也就无法对故障信号进行分析。

2) 改进消失矩高斯复小波由于消失矩得以优化，从而可以增强信号奇异点的检测能力，经邻幅比和相位畸变率对消失矩阶数进一步优化后，幅频特性中表征奇异性的幅值量级显著增大，波峰更为明显，由邻幅比可知干扰被抑制了17.84%，相位信息中相位畸变减小了4.12%，即提高了复小波对信号奇异点的敏感程度。

3) 选用改进消失矩的复小波进行故障测距，将幅值和相位信息结合起来，保留了实小波正交紧支和近似对称的优点，克服了实小波缺乏相位信息和频带混叠的缺点。由于准确的提取故障时间，而使得改进消失矩复小波测距结果的误差比普通消失矩的高斯复小波的测距结果误差减少6.06%，比实小波测距结果误差减少5.82%。

[1] Kasun N, Athula R, Randy W, et al. Traveling-wave-based line fault location in star-connected multiterminal HVDC systems[J]. IEEE Transactions on Power Delivery, 2012, 27(4): 2286-2294.

[2] Alberto B, Mauro B, Mauro D S. Continuous-wavelet transform for fault location in distribution power networks: definition of mother wavelets inferred from fault originated transients[J]. IEEE Transactions on Power Systems, 2008, 23(2): 380-388.

[3] Hanif L, Yaman E. A machine learning and wavelet-based fault location method for hybrid transmission lines[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 51-59.

[4] 韩伟, 吴杰. 基于小波变换的信号相关技术在电力电缆故障测距中的应用[J]. 电网技术，2005, 29(11): 69-72.

Han Wei, Wu Jie. Application of wavelet transform based signal correlation technique in fault location of power cable[J]. Power System Technology, 2005, 29(11): 69-72. (in Chinese)

[5] 姜林, 郭昕. 基于小波包分析电缆故障定位的研究[J]. 智能电网, 2015, 3(1): 39-42.

Jiang Lin, Guo Xin. Study of the cable fault location in OWTS based on wavelet analysis[J]. Smart Grid, 2015, 3(1): 39-42. (in Chinese)

[6] 陈祥训. 时域紧支正交复小波及其在电力系统的应用[J]. 中国电机工程学报, 1999, 19(1): 1-4.

Chen Xiangxun. Time frequency compactly-supported orthonormal complex wavelets and their application in power system[J]. Proceeding of the CSEE, 1999, 19(1): 1-4. (in Chinese)

[7] 陈祥训. 正交紧支复小波的生成及其在电力系统的应用[J]. 中国电机工程学报, 2000, 20(7): 84-89.

Chen Xiangxu. Complex compactly-supported orthonormal wavelets and their application in power system[J]. Proceeding of the CSEE, 2000, 20(7): 84-89. (in Chinese)

[8] 周登登. 复小波包变换及其在小电流接地选线中的应用[D]. 成都: 西南交通大学, 2010.

[9] 张瑜, 王红霞, 周战荣, 等. 不同消失矩的小波在小波矩量法中的应用比较[J]. 红外与激光工程, 2007, 36(2): 299-302.

Zhang Yu, Wang Hongxia, Zhou Zhanrong, et al. A comparison between the application of different vanishing moment for the wavelet moment methods[J]. Infrared and Laser Engineering, 2007, 36(2): 299-302. (in Chinese)

[10] 刘小峰, 张开飞, 赵玲. 复解析最优小波解调法[J]. 振动、测试与诊断, 2012, 32(5): 741-745.

Liu Xiaofeng, Zhang Kaifei, Zhao Ling. Optimization of complex analytical wavelet demodulation[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(5): 741-745. (in Chinese)

[11] Ingrid D. 小波十讲[M]. 李建平, 杨万年，译. 北京: 国防工业出版社, 2013: 5-25.

[12] Debi P M, Subhransu R, Samantaray G J, et al. A combined wavelet and data-mining based intelligent protection scheme for microgrid[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2295-2304.

[13] 简涛, 何友, 苏峰, 等. 奇异信号消噪中小波消失矩的选取[J]. 雷达科学与技术, 2006, 4(1): 31-35.

Jian Tao, He You, Su Feng, et al. Selection of vanishing moments of wavelet in denoising the signal with singularity[J]. Radar Science and Technology, 2006, 4(1): 31-35. (in Chinese)

[14] 胥永刚, 孟志鹏, 陆明. 双树复小波和ICA用于滚动轴承复合故障诊断[J]. 振动、测试与诊断, 2015, 35(3): 513-519.

Xu Yonggang, Meng Zhipeng, Lu Ming. Compound fault diagnosis of rolling bearing based on dual-tree complex wavelet packet transform and ICA[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(3): 513-519. (in Chinese)

[15] 葛耀中. 新型继电保护和故障测距的原理与技术[M]. 西安: 西安交通大学出版社, 2007: 181-189.