利用GRACE和地球物理模型研究地球动力学扁率变化

陈品馨

(测绘出版社，北京 100045)

旋转的地球在万有引力和离心力的共同作用下，形成一个南北极方向略扁、赤道方向稍长的旋转扁椭球体，其动力学扁率常用物理量J2表示。由于地球内部物质运动和全球气候变化等因素的影响，导致地球表面大气、海洋和陆地水等流体质量在时间和空间尺度上重新分布和运动，引起地球主转动惯量矩和地球自转角速度ω发生变化，进而引起地球动力学扁率J2变化，反映了地球内部物质重新分布与运动及其各圈层相互作用和耦合的过程[1-2]。

卫星激光测距 (satellite laser ranging ，SLR) 对重力场二阶带球谐函数系数较敏感，较好地估计了地球动力学扁率J2，在国内外得到了深入研究和广泛应用[1,3]。美国NASA和德国DLR合作于2002年3月发射低低卫星跟踪卫星“重力恢复与气候试验”GRACE卫星，提供了精度高1～2个数量级的重力场低阶项，充分展现了卫星重力学研究的主要功能和优越性[4]。虽然数据处理技术不断改进，但低阶球谐系数仍然不能精确确定，这在很大程度上是由任务设计引起[5]。

Swenson等于2008年研究了一种新方法来探测低阶位系数，它结合了GRACE数据和海底气压模型(ocean bottom pressure，OBP)，没有用到GPS观测数据。本文在研究Swenson方法的基础上，发展了一种新方法，使用GRACE月时变重力场模型系数、海底气压模型和冰期均衡调整模型(glacial isostatic adjustment ，GIA)估计C20月变化。该种方法采用的观测值密集且均匀分布，而且随着卫星观测及相关模型精度的提高，所得到结果的精度可进一步提高。本文将得到的结果与SLR的结果进行比较验证，二者的季节变化非常接近。

1 基本原理

由Swenson等的方法确定C20的公式为[10]

(1)

(2)

式中，a为参考椭球的长半轴；ρearth为地球的平均密度；kl表示1阶项的负荷Love数[13]。

(3)

其中，矩阵I可由式(4)求出

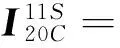
(4)

式中，矢量G可由式(5)求出

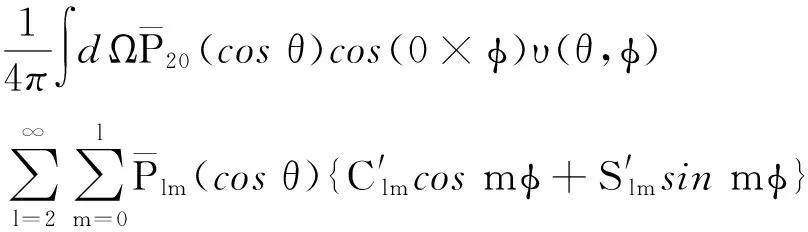
(5)

2 选用的数据、模型和方法

2.1 GRACE时变重力场模型

本文采用2003年1月至2012年12月的CSR RL05、GFZ RL05a、JPL RL05 GRACE 月重力场模型。所采用的模型均含有较大的误差，表现为南北走向的条带。为了解海平面方程统计自身引力和负载效应，需要尽可能准确地获取陆地负载的空间分布。因此，本文选用了经过DDK4滤波器滤波的时变重力场模型。DDK4滤波器是利用误差协方差矩阵解相关的滤波器，是一个先验信号协方差矩阵的球面函数域。通过这种方式，滤波器能确保越高频噪声和越低强度的信号，振幅减小得越慢。最后的效果类似于经验去条纹滤波和高斯滤波的结合。

2.2 海底气压模型和自引力效应

2.3 冰期均衡调整模型

式(2)所讨论的方法指出重力场变化仅仅是由地球表面质量的重新分配引起。因此，需要移除固体地球的贡献，如构造地质学方面和冰期均衡调整等。考虑了冰期均衡调整，移除的冰后回弹信号将被重新存储在最终的数据处理阶段[10]。由于冰后回弹模型为线性趋势，因此选择任意一种冰后回弹模型对季节性信号和其他短期信号都没有任何影响。

3 计算结果和分析

影响系数C20估计的因素有：①输入模型的选择(GRACE数据，海底气压模型OBP 和冰期均衡调整模型GIA)；②缓冲区宽度，GRACE产品数据所使用的滤波及是否考虑自引力效应SAL。通过对数据处理参数进行不同组合，本文解算得到了C20时间序列变化，与利用SLR数据得到的C20时间序列进行了比较。本文对偏差、线性趋势、一年及半年周期的时间序列进行了估计，并与SLR时间序列的相应参数进行了比较。

首先比较了去线性趋势和不去线性趋势的时间序列。与SLR方差的百分比计算定义为

(6)

式中，Model为本文所用的模型估计；<>为方差算子。本文与SLR结果中的年周期振幅和相位进行了比较。

图1和图2给出了去线性趋势的时间序列，以此说明本文使用不同模型和算法处理GRACE数据解的敏感度，SLR解用黑色实线表示。表1给出了不同模型算法的组合。海平面升降指的是由于海水质量变化导致的平均海水面变化(假设增加或减少的水是均匀分布在海面上的)。

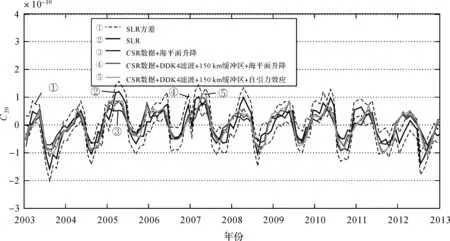
图1 使用不同方法和模型处理GRACE CSR RL05数据得到的C20解与SLR解比较(去线性趋势)

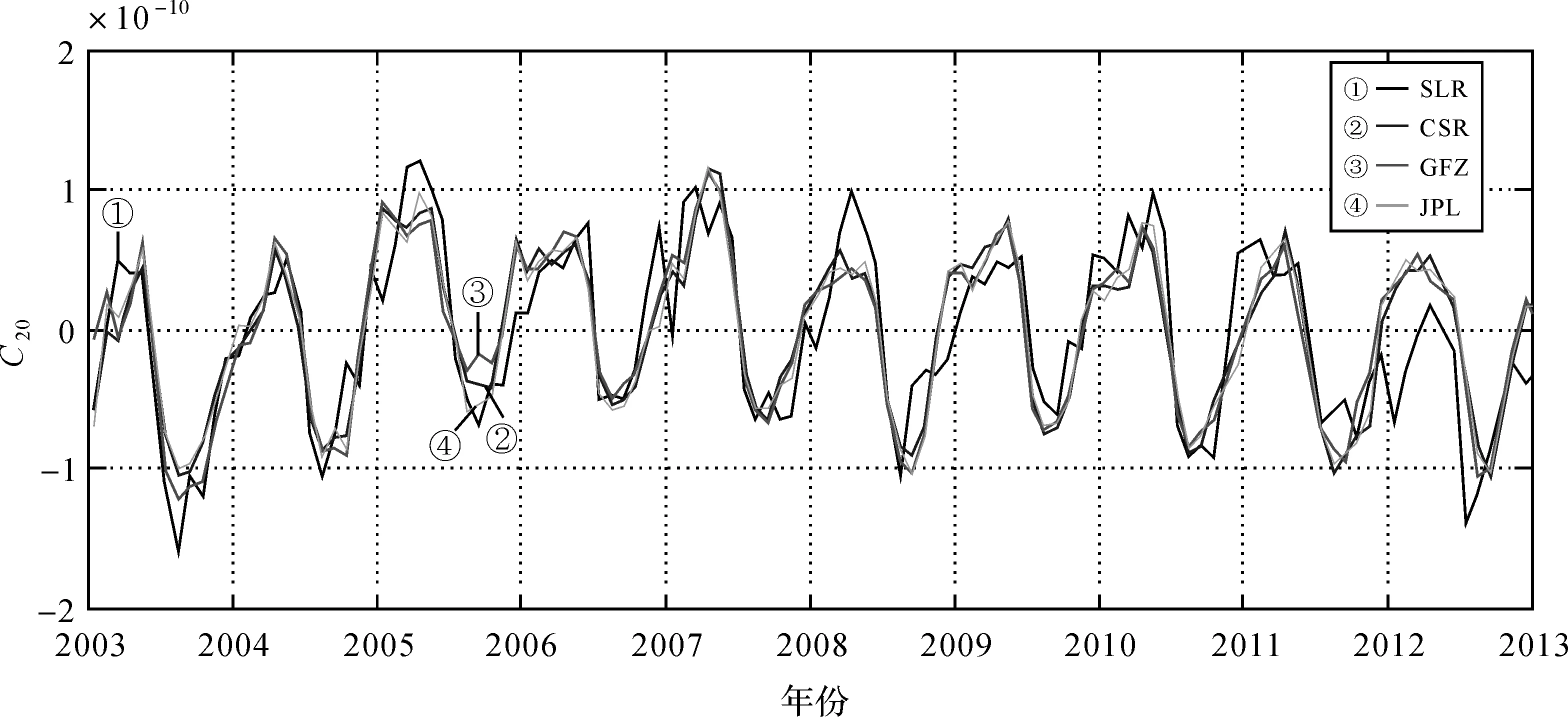
图2 使用不同GRACE数据的比较(均使用DDK4滤波、150 km缓冲区、自引力效应)

图1给出了使用不同方法处理GRACE CSR RL05的结果。不用缓冲区和忽略自引力效应(③)严重低估了季节性信号的振幅。但它与SLR时间序列的大部分特征是一致的，如其最大值和最小值的相对量和它的相位。它的结果59%在SLR方差范围内，年周期的相位也非常接近，但振幅明显小于SLR的结果。

在进行DDK4滤波，考虑海平面升降并且添加了150 km缓冲区(④)后，大大提高了振幅的整体匹配度。年信号的振幅统计值与SLR很相近，在2σ以内。这里整体匹配度的增加是比较合适的，它的结果67%在SLR方差范围内。如果将缓冲区的范围加到250 km或更大，反而降低了结果落在SLR方差范围的比例。这里选择不同的缓冲区可能对信号泄漏的处理影响不同。

最后用150 km缓冲区和考虑了自引力效应(⑤)进一步增加了落在SLR方差范围的比例，达到70%。同时对估计的年信号的振幅产生了明显的影响，这种方法所得结果与SLR结果最为匹配。计算自引力效应时考虑了地球自转的影响，但对于C20估计的影响很小。

从海洋项中去除缓冲区可避免沿海区域的自引力效应影响。本文比较了直接解算全海域的海平面方程和解算较小海域的海平面方程，将海洋项减去150 km的海岸线的范围得到较小海域，后者得到的年信号振幅增加了2%。

图2显示了使用不同方法处理不同GRACE数据的结果。GFZ的结果匹配度最好，70.9%落在SLR方差范围内，年周期信号振幅最相近。GFZ、CSR和JPL的结果非常相近，年周期信号振幅的统计结果均在1σ以内。

相位并未受到上述不同数据的影响。不同的相位估计与SLR结果的差别均在10 d之内。

4 结 论

本文利用GRACE月重力场模型、海底气压模型和冰期均衡调整模型等估计了地球动力学扁率月变化，结果表明，所得时间序列与卫星激光测距数据的结果差别不大。影响季节性信号振幅的主要因素是沿海区域信号泄露，本文就如何选用合适的缓冲区减少沿海地区的信号泄露进行了分析比较，解算的结果与SLR结果得到了很好的验证。

参考文献：

[1] COX C，CHAO B F.Detection of Large-scale Mass Redistribution in the Terrestrial System since 1998[J].Science，2002，297：831-833.

[2] CAZENAVE A，NEREM R S.Redistributing Earth’s Mass[J].Science，2002，297(5582)：783-784.

[3] YODER C K，WILLIAMS J G，DICKEY J O，et al.Secular Variations of Earth’s Gravitational HarmonicJ2Coefficient from Lageos and Nontidal Acceleration of Earth Rotation[J].Nature，1983，303：757-762.

[4] TAPLEY B D，BATTADPUR S，WATKINS M，et al.The Gravity and Climate Recovery Experiment：Mission Overview and Early Results[J].Geophysical Research Letters，2004，31(9)：48-54.

[5] CHEN JL，RODELL M，WILSON CR.Famiglietti JS (2005) Low Degree Spherical Harmonic Influences on Gravity Recovery and Climate Experiment (GRACE) Water Storage Estimates[J].Geophysical Research Letters, 2005,32(14):29-37.

[6] CHENG M，TAPLEY B D，RIES J C.Deceleration in the Earth’s Oblateness[J].Journal of Geophysical Research Solid Earth,2013,18(2):740-747.

[7] CHENG M，TAPLEY B D.Variations in the Earth’s Oblateness during the Past 28 Years[J].Journal of Geophysical Research：Solid Earth,2004,109(9):25-36.

[8] BLEWITT G，CLARKE P.Inversion of Earth’s Changing Shape to Weigh Sea Level in Static Equilibrium with Surface Mass Redistribution[J].Journal of Geophysical Research，2003，108(8)：2311-2319.

[9] KUSCHE J，SCHRAMA E J O.Surface Mass Redistrib-ution Inversion from Global GPS Deformation and Gravity Recovery and Climate Experiment (GRACE) Gravity Data[J].Journal of Geophysical Research，2005，110(7)：2461-2471.

[10] SWENSON S,CHAMBERS D,WAHR J.Estimating Geocenter Variations from a Combination of GRACE and Ocean Model Output[J].Journal of Geophysical Research：Solid Earth，2008：113(B8):2841-2849.

[11] GERUO A，WAHR J，ZHONG S.Computations of the Viscoelastic Response of a 3-d Compressible Earth to Surface Loading[J].Geophysical Journal International,2012,192(2):557-572.

[12] PELTIER W. Global Glacial Isostasy and the Surface of the Ice-age Earth：the ICE-5g (VM2) Model and GRACE[J].Annual Review of Earth Planetary Sciences, 2004,32(1):111-149.

[13] WAHR J，MOLENAAR M，BRYAN F. Time Variability of the Earth’s Gravity Field：Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J].Journal of Geophysical Research：Solid Earth,1998，103(B12):30205-30229.

[14] 张子占，陆洋，许厚泽.GRACE和SLR观测的地球动力学扁率最大熵谱及小波相关分析[J].地球物理学报，2007，50(5):1383-1389.

[15] 曲伟菁，吴斌，周旭华.根据人卫激光测距、GRACE和地球物理模型求解地球低阶重力场季节变化[J].测绘学报，2012，41(6):904-909.

[16] 金双根，张兴刚.GPS,OBP和GRACE估计地球动力学扁率变化及其地球物理激发[J].科学通报，2012(36):3484-3492.

[17] 曲伟菁.地球低阶重力场变化的研究[D].北京：中国科学院研究生院，2012.