数理统计在混凝土数据处理中的应用
2018-05-03李虎成
李虎成
(佳木斯佳宇建材有限公司,黑龙江 佳木斯 154002)
0 引言
数理统计是一门具有广泛应用的数学分支,它根据试验或观测得到的数据来研究随机现象,并对研究对象做出估计、判断。在混凝土的生产过程、质量控制、原材料检测、配合比试验中,会产生大量的试验数据。应用数理统计知识可以帮助分析和处理这些数据,从而得出结论以便优化生产,保证质量稳定性,预测试验结果等。数理统计方法在混凝土相关数据处理中具有广泛应用,包括误差分析、参数估计、假设检验、方差分析、抽样检验、控制图、回归分析、试验设计等。下面主要从假设检验、控制图及回归分析等几个方面结合实例介绍数理统计在混凝土数据处理中的应用。数据计算处理则借助 Excel 软件这一简便实用的工具。
1 基本概念
1.1 基本统计量
把试验的全部可能观测值称为总体。其中的每一个观测值称为个体。从总体中随机抽取一部分的个体称为样本。所有观测值的平均值就是总体的均值μ。但试验是有限次数的样本。常采用样本平均值来检验总体平均值和估计总体平均值,样本平均值(Excel 函数命令 AVERAGE)按下式计算:

式中:Xi为样本值。
采用总体方差 σ2来反映数据波动的大小,样本方差S2作为 σ2的无偏估计量用来估算总体方差。样本方差 (Excel 函数命令 STDEV)按下式计算:

σ 和S分别称为总体标准差和样本标准差,(Excel 函数命令 VAR)。
1.2 正态分布
正态分布又称高斯分布,是数理统计中非常重要的一种概率分布,混凝土强度波动,试验误差等许多随机变量都服从正态分布。若随机变量X服从平均值μ、方差 σ2的正态分布,记为X~N(μ,σ2)。其概率密度函数用下式表示:

当μ=0,σ2=1 时,称X服从标准正态分布(Excel函数命令 NORMSDIST),记为X~N(0,1)。标准正态分布密度函数为:

正态分布曲线是单峰对称曲线,最大值在 x=μ处。曲线拐点在 x =μ±σ 处。离平均值μ越近,概率越大,在 ±3σ 以外的概率仅约为 0.3%,几乎不可能发生,也就是所说的“3σ”法则,见图 1 。

图1 标准正态分布
2 假设检验
2.1 正态总体均值的假设检验
假设检验是在不知道总体的分布函数或者虽然知道分布函数形式,但不知其参数的情况下,为了推断总体的有些未知特性,提出某些对总体的假设。根据样本对所做出假设是接受还是拒绝的决策过程。假设检验在混凝土数据处理中具有非常广泛的应用。
例 1 某预拌混凝土企业生产 C25 混凝土,粗骨料采用 5~31.5mm 碎石,平均强度μ0=29.2MPa。因原材料短缺,粗骨料采用 5~31.5mm 卵石,在其他原材料相同的情况下,按同样的配合比成型 7 组混凝土,取得强度数据如下:27.8MPa,28.2MPa,31.2MPa,25.8MPa,29.6MPa,26.7MPa,28.3MPa。判断更换卵石后,总体平均强度是否有显著变化?(显著性水平为5%)
首先称“更换卵石后,总体平均强度也不变”这种假设为原假设,记作H0,与原假设对立的假设“更换卵石后,总体平均强度发生变化”称为备择假设,记作H1。对原假设进行检验叫做假设检验。本例中混凝土抗压强度X符合正态分布,即X~N(μ,σ2),这里均值μ和方差 σ2均未知,问题是根据样本值判断μ=29.2 还是μ≠29.2,属于正态总体均值的假设检验。
设H0:μ = μ0,H1:μ ≠ μ0
当方差 σ2未知时采用 检验法,计算检验统计量:

算得=28.2MPa,S=1.8MPa。
应用t检验
查t分布表得t0.025(6)=2.45>t=1.44,所以接受假设H0,即更换卵石后,总体平均强度没有显著变化。以上检验法称为t检验法,其中t分布统计值t0.025(6) 也可以在 Excel 输入函数命令 [=TINV(0.05,6)] 得到。t检验法适用于总体方差 σ02未知的情况。
2.2 正态总体方差的假设检验
2.2.1 单个总体的情况
对于符合正态分布的总体X~N(μ,σ2),μ, σ2均未知,要求检验假设(显著性水平为α)

作为统计检验量,拒绝域为

以上检验法称为2χ检验法,分布函数2χ称为卡方分布。
例 2 某预拌混凝土公司质量稳定,C30 混凝土 28d抗压强度长期服从方差 σ2=2.7MPa 的正态分布,该公司五月份生产取用了新开采的江砂,含水率波动较大。现从五月份该批 C30 混凝土随机取样 26 组试样,测得其样本方差S2=3.5MPa。判断根据这一数据能否推断该批混凝土的抗压强度波动性较以往有显著的变化(取显著性水平α=0.05)。
设H0: σ2=2.7,H1: σ2≠2.7
n= 26,其中2χ统计值可以查表求得,也可以在 Excel 输入函数命令[=CHIINV(0.025,25)] 求得。同样方法得到代入式 (7)得到拒绝域为

由S2=3.5 得所以拒绝H0,结论为该批混凝土抗压强度波动性较以往具有显著性变化。
2.2.2 两个总体的情况

由数理统计知识,我们取

作为统计检验量,拒绝域为
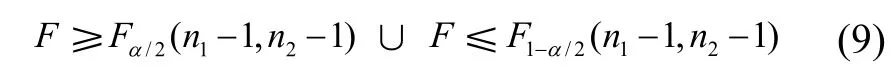
以上检验法称为F检验法。
例 3 某混凝土搅拌站在校准称量系统前取得 21 组抗压强度数据,样本标准差S1=3.6MPa,校准后取得相同配合比的强度数据 16 组,样本标准差S2=1.9MPa。判断校准前后混凝土均匀性是否具有显著差异(显著性水平α取 0.05).
n1=21,n2=16,Fα/2(n1-1,n2-1) =F0.025(20,15) = 2.756,其中F统计值可以查表求得,也可以在 Excel 输入函数命令[=FINV(025,21,15)] 求得。同样方法得到F0.975(20,15) = 0.259。代入式 (9) 可得拒绝域为
F≥2.756 和F≤0.259 的并集。
结论为校准前后混凝土均匀性具有显著差异。
3 控制图
3.1 控制图介绍
控制图也称休哈特控制图。是由沃特.休哈特(Walter A.Shewhart)博士于 1924 年首先提出的一种实用管理方法。它将显著性统计原理应用于生产过程,通过作图方法来了解生产过程的稳定性。控制图方法在欧美、日本等发达国家得到广泛应用,美国混凝土学会(ACI)及日本建设省也早已将其纳入混凝土相关规范。
由正态分布可知,样本值落在μ±3σ 之外的概率仅约为 0.3%,几乎不可能发生。如果发生了,则说明生产过程有系统因素存在。管理图的作用在于判断在生产过程的受控状态,区分系统因素和偶然因素,当样本点出现在控制限以外,则说明生产出现异常,需要及时查找原因并通过组织、管理、经济、技术等措施消除异常,保持生产过程的稳定性。控制图的判断准则就是μ±3σ。图 2 中平均值μ称为中心线 CL;μ+σ 称为上控制限 UCL;μ-σ 称为下控制限 LCL。控制图分为计量管理图和计数管理图,在混凝土数据处理中,一般采用计量管理图,即管理混凝土强度、含气量、坍落度、容重等统计量。计量管理图中,以混凝土抗压强度为例常用均值图与极图R图或标准差S图。

图2 管理图判断准则
由于在实际生产中μ与 σ 通常未知,并不能简单通过μ±3σ 来作出控制图,可以通过总均值来估计μ作出中心控制线 CL;根据样本的极差或者标准差来估计 σ 作出 UCL 线和 LCL 线。表 1 是 GB/T 4091—2001《常规控制图》(以下简称《控制图》)给出的相应控制限公式。其中A2、A3、D4、B4等为常数,可以通过《控制图》内的表 2 查得。

表1 控制图控制限公式
3.2 应用实例
例 4 表 2 为某预拌混凝土企业 2017 年七月份连续生产的同一配合比混凝土 28d 抗压强度样本数据共计25 组,作出该月混凝土的平均值图。

表2 混凝土 28d 抗压强度数据 MPa
其中子组数k为 25,
中心线CL==36.1MPa;上控制限UCL=X+A3= 36.1+1.954×1.66=39.4MPa;下控制限LCL=-= 36.1-1.945×1.66=32.9MPa。这里由子组内样本数n=3,在《控制图》标准表 2 中查得A3为 1.945。
在 Excel 中选择“插入”—“图表”—“折线图”可以方便的画出平均值图,见图 3。

图3 混凝土 28d 抗压强度平均值图
画出之后,可以根据《控制图》中第 7 款的八个模式检验示意图来判断生产过程的稳定性。
4 回归分析
4.1 一元线性回归
回归分析是确定当自变量x变化时,因变量 Y 大体按照某种规律变化的一种数理统计方法。其在混凝土数据处理中具有广泛应用,在试验数据处理、求得经验公式、产品质量控制等许多方面,回归分析是一种有力的方法。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,则这种回归称为一元线性回归分析。一元线性回归模型为:
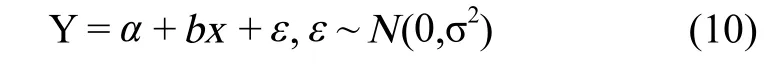
其中ε为随机变量,b称为回归系数。
通常使用最小二乘法求出一条直线,使试验点离这条直线纵坐标距离的平方和最小,称这条直线方程为回归方程:


对于一些非线性关系,也可以通过变量代换转化成线性关系而求得回归方程。
4.2 应用实例
例 5 某次混凝土凝结时间试验测得表 3 中试验数据,求该批混凝土的初、终凝时间。
试验证明,混凝土贯入阻力与凝结时间的关系符合幂函数关系,即:

式中:t——时间,min;
fPR——贯入阻力,MPa;
c、k ——经验系数。
其属于非线性回归关系,对公式 (14) 两边取自然对数,并移项,按照 GB/T 50080—2016《普通混凝土拌和物性能试验方法标准》的要求以 lnfPR为自变量、lnt
为因变量得到:


式中α、b——最小二乘估计值。
当贯入阻力为 3.5MPa 时的t为初凝时间ts,贯入阻力为 28MPa 时t为终凝时间te:

采用 Excel 中的散点图及趋势线可以较方便的求解出回归方程为 y = 0.1298 x + 6.3843,见图 4。

表3 混凝土凝结时间实测数据

图4 混凝土凝结时间曲线图
回归系数α=6.3843,b=0.1298。将贯入阻力取 3.5MPa 带入初凝时间公式 [Excel 函数命令为=EXP(B11+B13*LN(3.5)),B11 为回归系数α所在单元格,B13 为回归系数b所在单元格],得初凝时间ts为697min,同样方法求得终凝时间te为 913min。
将非线性回归转化为线性回归处理时,不能用变换成直线后的线性相关系数 r 来判断曲线拟合的效果,应该直接根据实测值yi与回归曲线上相应估计点来计算剩余平方和,此时有:

R2称为相关指数,以区别于相关系数r,R2越接近1,表示曲线拟合得越好。本例中用 Excel 可以直接求出R2=0.9926,显示拟合的效果比较好。
5 总结
符合正态分布的随机变量在混凝土数据中随处可见,一般来说对非正态分布的随机变量当样本数n的数量足够大时,根据大数定律与中心极限定理也可以当做正态分布来处理,这也是正态分布应用广泛的原因。假设检验中的t分布,2χ分布及F分布统称为三大分布,是符合正态分布随机变量抽出的样本的分布,在数理统计中占有重要地位。
控制图的作用在于区分偶然因素与系统因素,并以±3σ 作为上下控制限。如果只有偶然因素,在 1000 次试验中只会出现 3 次,是几乎不可能超出控制限的,如果发生超过控制限的点,可以判定不是偶然因素引起的,这在数理统计中称为小概率事件原理。
回归分析主要研究变量之间是否具有一定的关系。如果存在关系,则选择适当的函数表达式来描述变量之间关系的密切程度。一元线性回归是指一个因变量与一个自变量的关系,它们之间的关系通过散点图判定有线性趋势,可以建立回归直线。对于非线性关系,通常将观测点分布形状与函数图像相比较,选择某些函数类型,再对变量做适当变换,可以转化成线性回归问题。
[1] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008.
[2] 蒲括,邵鹏.精通 Excel 数据与分析[M].北京:人民邮电出版社,2014.
[3] GB/T 4091—2001.常规控制图[S].
[4] (澳)肯·戴.混凝土配合比设计、质量控制与规范[M].曾力译.北京:中国建材工业出版社,2011.
[5] GB/T 50080—2016.普通混凝土拌合物性能试验方法标准[S].
