声子角动量与手性声子∗

俞杭徐锡方牛谦张力发

1)(南京师范大学物理科学与技术学院,南京 210000)

2)(德克萨斯大学物理系,奥斯汀,德克萨斯 78712,美国)

1 引 言

1.1 爱因斯坦-德哈斯效应

爱因斯坦-德哈斯效应是一种由磁化强度变化引起力学转动的现象,如图1,最初的实验设计是用来证明安培分子电流的存在,这是爱因斯坦一生中惟一的实验,是和德哈斯一起完成的.爱因斯坦认为,原子内电子绕原子核的运动和电子自旋形成了“分子电流”,这是物质磁性的来源.原子磁矩

与总角动量J=mvr的比值称回磁比

其中g是朗德因子,他们认为,其理论值应该为1.实验结果有1.02和1.45等.他们发表的结果为1.02,验证了分子电流的假设,这就是爱因斯坦-德哈斯效应.然而,后来的实验表明g≈2,间接验证了后来发现的电子自旋(验证电子自旋的经典实验——斯特恩盖拉赫实验要晚于这一系列实验),在铁磁体中原子磁矩的主要贡献来自电子自旋磁矩而非轨道磁矩[1].

根据磁矩与角动量的关系以及角动量守恒,

爱因斯坦-德哈斯效应提供了一种测量各种材料回磁比的有效方法,回磁比的精确性是确定轨道和自旋对总磁矩贡献的关键.但是宏观可见的力学转动仅反映刚体的运动,而声子——原子在平衡位置附近的振动,传统认为是没有角动量的,所以在爱因斯坦-德哈斯效应中没有被考虑.如果存在非零的声子角动量,那么总角动量中必须考虑声子的贡献,从而回磁比需要修正.

图1 自由悬挂的铁磁体因磁化强度的改变而发生转动Fig.1.A mechanical rotation of a freely suspended body caused by the change in its magnetization.

1.2 声子霍尔效应

在发现电子霍尔效应后,Leduc[2]认为金属热传导也具有相似的行为,当施加温度梯度时有横向热流产生,这就是热霍尔效应或Righi-Leduc效应.这是由于电子对热传导的贡献,自由电子受洛伦兹力的直接结果.在电绝缘的晶体中,声子是热流的载体,这与金属中的情况不同,金属中的主要载流子是电子.在2005年,Strohm等[3]在顺磁绝缘体中发现了声子霍尔效应,随后由Inyushkin和Taldenkov得以重复[4].如图2所示,它们发现在有纵向温度梯度的顺磁绝缘体薄膜上,加上垂直的磁场后,在薄膜内垂直于纵向温度梯度方向上观察到横向温度差.声子霍尔效应(PHE)是一项令人惊喜的发现,因为声子作为中性准粒子不能直接与磁场相互作用而受到洛伦兹力,这一新颖的发现使磁场成为操纵声子的另一个自由度.

图2 声子霍尔效应示意图:热流方向在磁场作用下发生偏转[8]Fig.2.Phonon Hall e ff ect:the direction of the heat lf ow is de fl ected by the magnetic fi eld[8].

自那以后,人们提出了一些理论解释[5,6],通过考虑自旋声子耦合来理解PHE.磁场不能直接作用在声子上,只能使顺磁离子极化,正是声子与携带磁矩的顺磁离子之间的耦合引起了声子霍尔效应,又被称为拉曼自旋声子相互作用.所以磁场可以施加一个有效的力来改变声子输运过程,产生了涡旋的热流[7].所以一个自然的问题就是,这种涡旋的声子流是否具有非零的角动量,并且伴有一些新的宏观效应.

2 声子角动量与声子圆极化[9]

对应于力学转动的晶格角动量

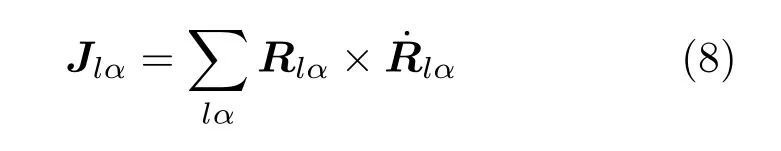
仅反映了刚体运动,这里通过质量归一化来简化角动量的形式.在微观图象中,类似于晶格角动量(刚体部分),声子角动量可以定义为原子偏离平衡位置的位移与速度的叉积:

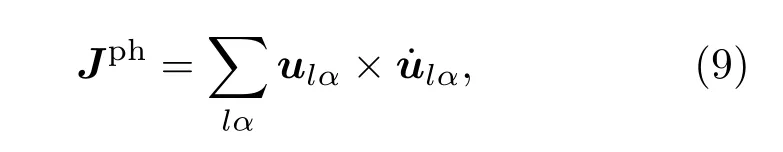
ulα是第l个原胞里第α个原子的位移,将位移表示为二次量子化的形式

得到平衡态下沿z方向的总声子角动量

和每一种声子模的角动量

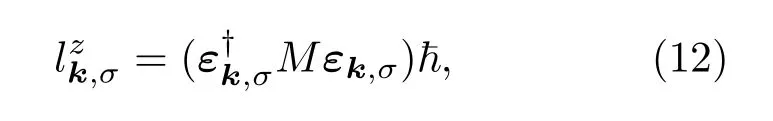
意味着每一种声子模式(k,σ)除了有零点能量～ωk,σ/2,还有非零的角动量

另一方面,类比于量子理论中对光子偏振态的表示方法,可以定义声子偏振态[2].考虑原胞内含有n个原子的一般性系统,声子模的本征矢为这里仅考虑二维平面内的圆极化情况.可以用子晶格的左旋或右旋偏振态来定义一组新的基矢

声子模本征矢按照这组基矢展开

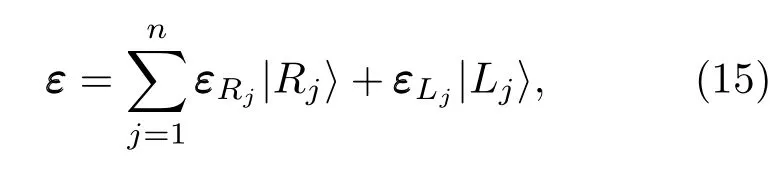
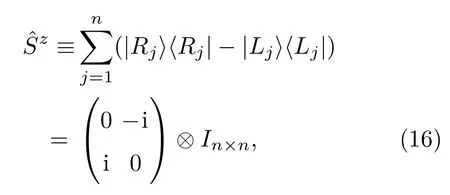
具有如下性质

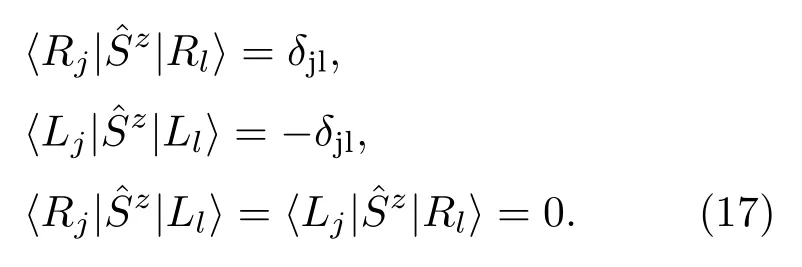
声子圆极化的大小为

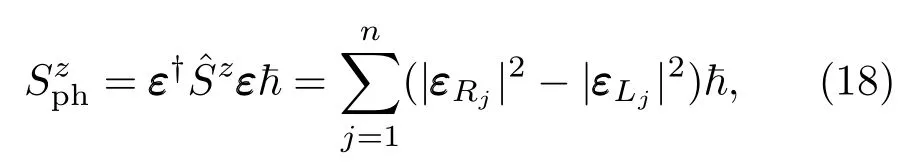
3 声子角动量与对称性分析

考虑对称性可以发现,当系统具有时间反演对称性时,声子角动量满足而当系统具有空间反演对称性时,声子角动量满足对于一个同时具有时间空间反演对称性的系统,声子角动量必为零可见非零声子角动量存在于时间反演对称性被破坏或空间反演对称性被破坏的系统中.下面将讨论在磁性系统中通过引入自旋声子相互作用,破坏时间反演对称性,但是保持空间反演对称性,总的声子角动量不为零;在非磁性六角格子系统中通过引入AB晶格,破坏空间反演对称性,但是保持时间反演对称性,在布里渊区高对称点处声子是圆极化的,具有手征性.

4 磁性系统中的声子角动量

4.1 磁性系统中的声子角动量

对于处在均匀外磁场中的离子晶体,哈密顿量[5,6]写为

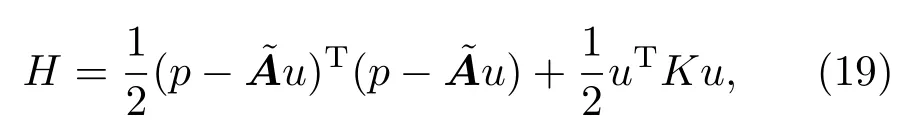
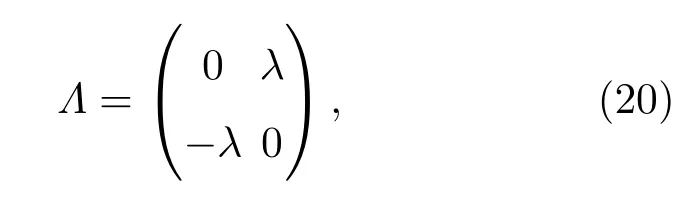
λ具有频率的量纲,正比于自旋声子相互作用和磁化强度.

当体系不存在自旋声子相互作用时,哈密顿量简化为

可得每一种声子模的角动量关系

4.2 二维晶格声子角动量的数值计算[9]

图3 (a)在T=0 K下不同晶格对称性下原胞的声子角动量Jphz随λ的变化;(b)原胞的声子角动量Jphz随温度T和λ的等值分布;(c)在λ=1 THz条件下不同声子能带的原胞声子角动量Jphz随温度T的变化,箭头指示模型的德拜温度(TD=358 K);(d)在T=0 K条件下不同能带的原胞声子角动量Jphz随λ的变化;图(b)—(d)是对蜂窝状晶格计算的声子角动量,所有声子角动量的单位是～[9]Fig.3.(a)The phonon angular momentumJphzof one unit cell as a function ofλat temperatureT=0 K for different lattice symmetries;(b)the contour plot of the phonon angular momentumJphzof one unit cell as a function ofλand temperatureT;(c)the phonon angular momentumJphzof one unit cell from different phonon bands as a function of temperatureTatλ=1 THz,where the arrow denotes the Debye temperature of the model(TD=358 K);(d)the phonon angular momentumJphzof one unit cell from different phonon bands as a function ofλatT=0 K.The phonon angular momenta in(b)–(d)are calculated for a honeycomb lattice.All the phonon angular momenta are in the unit of～[9].

如图3(a),在绝对零度T=0 K下,对于不同晶格对称性,总的声子角动量与λ的数值关系表明,honeycomb晶格和kagome晶格比三角形和正方形晶格有更大的声子角动量,这意味着每个原胞里有更多格点的晶格具有更大的声子角动量.可以由光学支对声子角动量的贡献比声学支更大来理解这一趋势.如图3(c)和图3(d),在低温下,如果λ不大,来自声学支的声子角动量在低温下消失,所以光学支对总的声子角动量占主要贡献.每个原胞里有越多的格点,就存在越多的光学支,所以声子角动量更大.如图3(a),总的声子角动量随着λ的增加而增加.如图3(b),因为λ正比于磁化强度,所以当磁化强度变号时,声子角动量也变号

这可以解释声子霍尔效应中当磁场反向时横向温度差反号的现象.

在高温极限下,由于

声子角动量趋于零,无论是否施加磁场,每个原胞的声子角动量随温度的升高而减小且在高温极限(温度远大于德拜温度)下趋于零.随着温度的升高,更多声子模式被激发,这些模式的角动量与零点角动量方向相反;在高温极限,所有激发模式正好与零点角动量抵消.可以如下理解经典极限条件下声子角动量的消失:在高温下,经典统计力学适用于计算声子角动量;对量子态的叠加变成在动量和位置相空间的积分,通过变量代换可以变为简谐系统,如前面的讨论,声子角动量为零;而且,Bohr-van Leeuwen定理阐明了在经典力学中平均磁化强度总是为零,使得经典极限条件下声子角动量消失.所以,声子角动量仅在低温量子系统中有意义.

4.3 回磁比的修正

该效应展示了一个自由悬挂的物体由于其磁化强度的改变而产生力学转动.在实验中,爱因斯坦和德哈斯采用了共振的方法,磁场是周期性的且调节为悬挂物的本征频率.这提供了测量磁化强度改变量与总角动量改变量的比值的方法.一般认为,系统的总角动量等于晶格角动量、自旋角动量、轨道角动量之和,

所以由于角动量守恒,可以得到晶格角动量的改变量等于自旋、轨道角动量改变量之和的相反数,

而晶格角动量的变化由样品的机械转动决定.但是从微观的观点,平衡状态下样品原子的角动量等于晶格角动量与声子角动量之和.所以总角动量要多一项声子角动量[9],

如前面的讨论,当存在自旋声子相互作用时,总的声子角动量不为零,根据角动量守恒,

另一方面,可以测量磁化强度的改变

4.4 观察声子角动量的实验设想

声子对总角动量有重要的贡献,而声子角动量的大小取决于λ的值.λ可以从色散关系得到,因为计算表明当存在自旋声子相互作用时,面内的简并声子模在Γ点劈裂,比如,对于两支面内的简并声学支,一支在长波极限时频率仍为零,而另一支频率为2λ.这种简并声学模的劈裂,可以通过中子非弹性散射或拉曼散射测得.当顺磁材料中磁化强度饱和时可以观察到更大的声子角动量,因为λ正比于磁化强度.在声子霍尔效应实验中,顺磁绝缘体用于凸显热输运中声子的贡献,而可以忽略电子和磁振子的贡献.但是,自旋声子相互作用广泛存在于各种磁性材料中[13].铁磁材料有非常大的磁化强度,如果自旋声子相互作用较强的话,则可以观察到明显的声子角动量.

对于有强自旋声子相互作用和较大磁化强度的材料,零点声子角动量是重要的.根据以往的研究,在一些铁磁材料中计算得到的轨道磁矩仅是总磁矩的很小一部分,就是说轨道角动量大约是～乘上一个很小的值[14].声子角动量与电子轨道角动量的大小是可以相比的,所以声子角动量不能忽视.

在铁磁绝缘体中,电子的输运是可以忽略.由于声子角动量随温度的升高而减小且在经典极限条件下趋于零的性质,可以在低温和高温下测量晶格角动量的改变,来分离出声子角动量,这里低温和高温的分界线应为德拜温度,它是划分量子和经典区域的临界温度.另一方面,为了避免磁振子的参与,除了要高于德拜温度,还需要低于居里温度.这就要求居里温度必须比德拜温度高很多.所以磁振子的角动量几乎不变,而声子角动量随温度有显著的变化,幸运的是许多铁磁材料可以满足它们的居里温度大约是1000 K,而它们的德拜温度低于500 K.

除了在测量回磁比中的应用,非零声子角动量也提供了研究磁性材料自旋声子相互作用的有效方法.另一方面,如何分离出铁磁材料中声子和磁振子对热霍尔效应的贡献是一个开放的问题,而声子角动量给出了获得声子贡献的一种方法.

5 非磁性系统中的手性声子

5.1 能谷对比电子学

由于空间反演对称性的破坏,导致动量空间分开的能谷K,K′不再等价,这种不等价性可以通过贝里曲率或轨道磁矩来描述,这两处能谷就构成了除电荷和自旋以外电子的另一个自由度.因此,能谷自由度的构筑依赖于材料体系空间反演对称性的破缺.能谷自由度的产生导致了能谷对比电子学的出现.

自然界中存在着许多类似于石墨烯的六角晶格层状材料,如氮化硼、过渡金属二硫化物、硒化镓等.不同于石墨烯,这些材料中的A和B子晶格分别由不同的原子构成,破坏了空间反演对称性,从而能谷自由度存在.这些材料为能谷电子学的研究创造了条件.

在AB堆叠的双层石墨烯材料上施加垂直于二维平面的电场,从而打破石墨烯晶格的空间反演对称性,导致在K和K′能谷产生大小相等但反向的贝里曲率及轨道磁矩[15].这种与能谷相关的贝里曲率及轨道磁矩带来了一些新奇的效应,比如能谷霍尔效应及与能谷相关的光学跃迁选择定则[16].如图4,由于贝里曲率反向使得K和K′能谷的电子在垂直于外加电场方向的运动发生横向且方向相反的偏转,这就是谷霍尔效应.与能谷相关的光学跃迁选择定则即能谷的圆偏光双色性,如图5,对应于K′(K)能谷中电子的带间跃迁只能是左旋(右旋)圆偏振态的光子参与.这些都为调控特定能谷态提供了可能的物理方法.

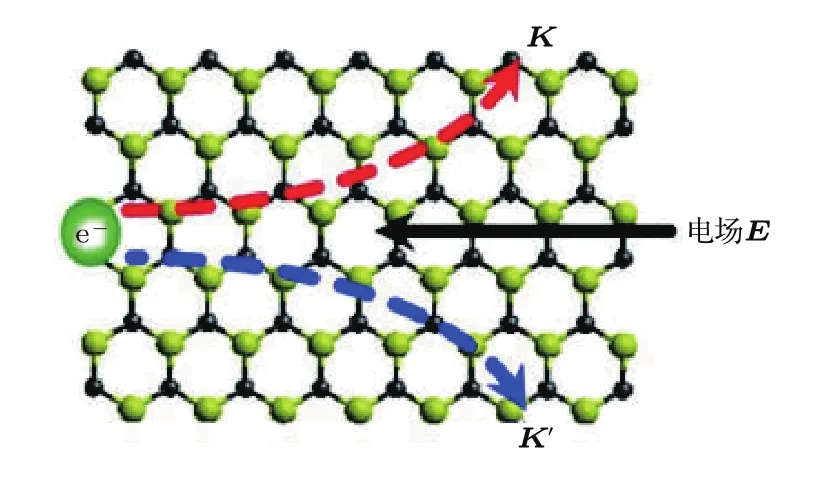
图4 谷电子霍尔效应示意图[16]Fig.4.Valley electronic Hall effect diagram[16].

由于谷内电子带间散射涉及极化的光激发和光致发光,而布里渊区边界的(谷)声子也参与谷间电子散射[17].鉴于在能谷处电子有确定的手性,自然要提出两个问题,谷声子是否有手性,在电子谷间散射中手性声子扮演了什么角色.后来在对过渡金属二硫化物(TMD)材料的实验中观察到光极性反转的现象[18],在该过程中发现布里渊区中心声子可以完全反转入射光子的极性.这一发现暗示了除谷声子外,参与电子谷内散射的Γ点声子也具有手性.所以研究布里渊区高对称点处的手性声子是有必要的.

图5 能谷光选择定则:σ+(σ−)圆极化光只与能谷K′(K)的带边沿跃迁耦合[16]Fig.5.Valley optical selection rules:σ+(σ−)circularly polarized light couples only to bandedge transitions in valleyK′(K)[16].

5.2 二维蜂窝状AB晶格的圆极化谷声子

5.3 高对称点处声子的赝角动量

为了研究手性声子, 首先关注二维蜂窝状晶格模型, 每个原胞有两种原子A 和B [19]. 蜂窝状AB晶格可以作为一个简化模型来反映空间反演对称性破缺的单层材料中手性声子的一般特征, 比如同位素掺杂[20]或交错晶格势下有带隙的石墨烯[21]、六角氮化硼[22]. 在蜂窝状晶格中, 在高对称点K,K′,处, 声子绕垂直于二维晶格平面的z 方向进行三重分立旋转是不变的, 本征矢有相位的改变,

图6 蜂窝状AB晶格的谷声子 (a)蜂窝状AB晶格的色散关系,图中显示了A,B子晶格的原胞中在K′点(kx=和K 点声子的振动情况,其中a是晶格常数,1到4标记了四个能带;圆半径表示振幅,相位和振动方向也包括在图中;(b)A,B子晶格在K′点和K点处非局域部分的相位关系示意图;(c)带1到带4在K′和K 点的声子赝角动量;这里纵向弹性常数为KL=1,横向弹性常数为KT=0.25,A原子质量为mA=1,B原子质量为mB=1.2;基矢量为(a,0)和声子能量为ε=～ωph[19]Fig.6.Valley phonons in a honeycomb AB lattice:(a)Phonon dispersion relation of a honeycomb AB lattice,the insets show phonon vibrations for sublattices A and B in one unit cell at K′and Ka is lattice constant,numbers 1 to 4 denote four bands.The radii of circles denote vibration amplitudes,phase and rotation direction are included;(b)phase correlation of the phonon nonlocal part for sublattice A(upper two panels)and sublattice B(lower two panels)at K′(left panels)and K(right panels);(c)phonon pseudoangular momentum(PAM)for bands 1 to 4 at valleys K′and K.Here,the longitudinal spring c onstant KL=1,the transverse one KT=0.25,and mA=1,mB=1.2.The primitive vectors are(a,0)andand the phonon energy is equal to～ωph[19].

轨道赝角动量由三重旋转下eiRRRl… kk相位的改变得到.在能谷K,K′,子晶格A,B的轨道赝角动量方向相反且取值为1或−1.在Γ点,两个子晶格均没有相位的改变,所以A,B的轨道赝角动量为0.自旋赝角动量由三重旋转下εk相位的改变得到.在能谷K,带1和带4子晶格A,B的自旋赝角动量分别为−1,1和1,−1,带2子晶格B的自旋赝角动量为−1,带3子晶格A的自旋赝角动量为1.在Γ点,存在两重简并的声学模和两重简并的光学模,单个模式不具有极化,但是,通过简并模的叠加,可以得到圆极化声子.

声子的赝角动量等于A子晶格的自旋和轨道赝角动量之和,也等于B子晶格的自旋和轨道赝角动量之和

由前面得到的K,K′处A,B原子的轨道、自旋赝角动量可以验证(34)式,并列于图6(c).如果其中一个子晶格不振动,则由另一个振动的子晶格决定.在Γ点,因为轨道赝角动量为0,声子赝角动量等于A子晶格的自旋赝角动量,也等于B子晶格的自旋赝角动量.通过两重简并模的叠加,子晶格做同样的圆极化振动,左旋或右旋.所以,两重简并模的声子赝角动量可取1或−1.

在高对称点具有三重旋转对称性,非简并声子模的赝角动量必是1,−1,0.因为三重旋转中心可以选在一个原胞里的任一个子晶格处,当该子晶格的轨道赝角动量为0时,子晶格的自旋赝角动量必等于声子赝角动量;就是说,它必是1,−1,0.所以,在能谷处的所有声子模,子晶格A,B必做圆极化振动;否则,不振动.

5.4 电子谷内谷间散射的选择定则

5.4.1 TMD中光极性反转现象

电子沿垂直于平面z方向的力矩为,在三重旋转下状态不变,赝角动量由子晶格A,B的轨道决定.如果假定价带对应电子位于子晶格A的轨道,而导带对应电子位于子晶格B的轨道,可以得到导带和价带的赝角动量lc(v)=±τ,τ=±1.所以,在有带隙的石墨烯中电子吸收右旋或左旋圆极化光子发生带间跃迁,由于赝角动量守恒,可以得到选择定则

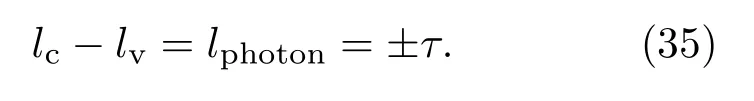
导带角动量与价带角动量之差等于光子角动量,如图7.

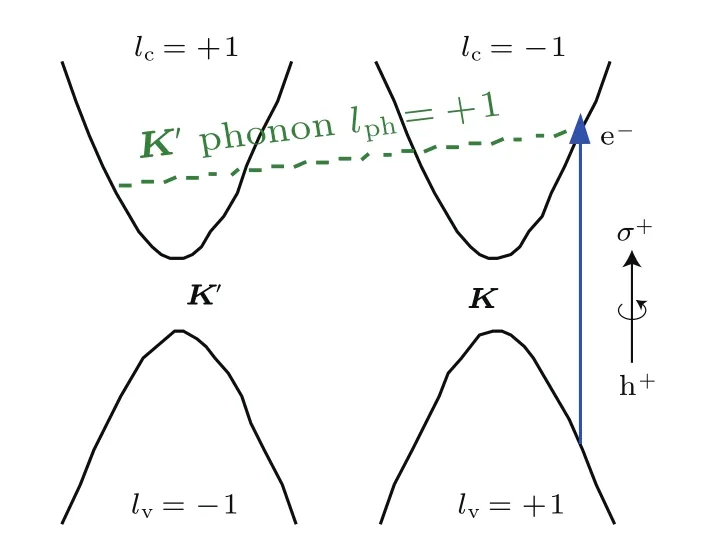
图7 电子谷间散射的选择定则Fig.7.Selection rules in electronic intervalley scattering.

在导带中的电子受到Γ点声子的谷内散射,然后发射另一个光子与价带的空穴结合,这一过程叫一级拉曼散射.在这个过程中,因为赝角动量守恒,选择定则为

光子角动量的改变等于声子赝角动量.在Γ点的两重简并光学模是拉曼激活模式,有赝角动量1,−1,所以可以预料在蜂窝状晶格(如有带隙的石墨烯或单层氮化硼)中有一个极性反转的拉曼G峰.在整个过程中,入射的右旋(左旋)光子吸收一个右旋(左旋)声子或发射一个左旋(右旋)声子,然后变为左旋(右旋)光子[19].这一选择定则解释了TMD中光极性反转的现象,如图8.

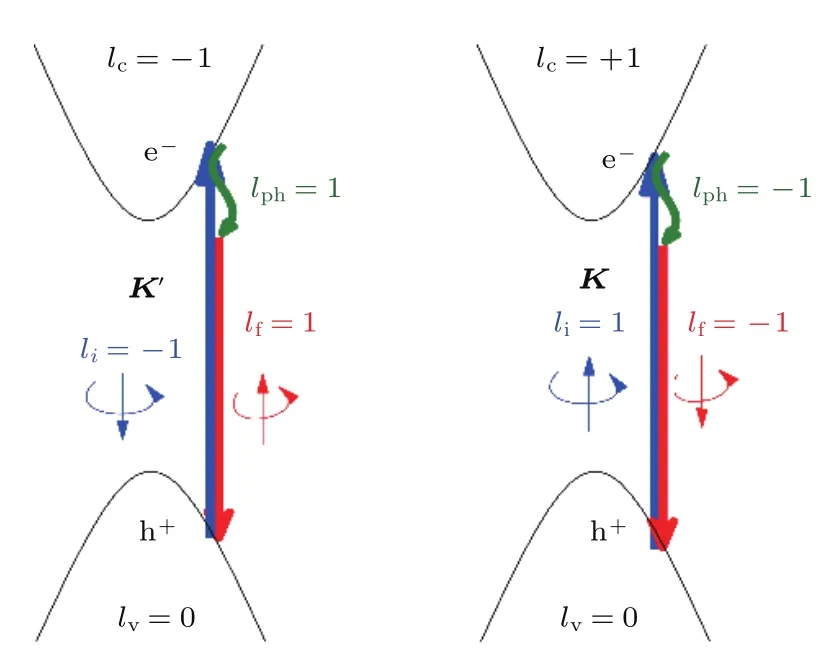
图8 Γ点声子改变光极性(a)能谷K′处左旋光极性反转;(b)能谷K处右旋光极性反转Fig.8.Photon helicity changed by phonons atΓ(a)lefthanded photon changes its helicity atK′valley;(b)righthanded photon changes its helicity atKvalley.

5.4.2 电子能谷间散射

如图7,通过发射一个圆极化的谷声子(lph=±1)可以实现电子的谷间散射,由于声子在三重旋转对称性下具有赝角动量,在同时满足动量和能量守恒的条件下,可以得到遵从赝角动量守恒的选择定则

K点导带(价带)角动量与K′点导带(价带)角动量之差等于该谷声子的赝角动量.众所周知,石墨烯拉曼光谱的双共振峰D反映了邻近K点声子的谷间散射[23,24].所以,根据拉曼光谱可以产生一个有明确赝角动量和频率的谷声子[19].

5.4.3 二硫化钼的谷间散射

有自旋轨道耦合的二硫化钼(单层转变为直接带隙)有带隙∆=1.65 eV且在能谷K的价带顶有λK,v=150 meV的自旋劈裂.而在导带底有3 meV的劈裂,相比可以忽略.通过吸收或发射光子,可以观察到谷声子参与电子谷间散射,满足赝角动量守恒和能量守恒的选择定则为电子角动量的改变等于声子和光子角动量的代数和,价带自旋劈裂等于声子能量和光子能量的代数和.

对于单层二硫化钼,在能谷处导带的赝角动量是1,−1,而价带是0[25].右旋极化光子激发了能谷K的一对激子(导带电子和价带空穴),右旋光子具有带隙的能量.因为激发的电子在能谷中心处,且声子具有能量,所以不能发射一个声子而被散射到另一个能谷中心.但是,由于价带有较大的自旋劈裂,空穴可以通过吸收一个受激圆极化光子并且发射一个手性谷声子而被散射到另一个谷,这里电子的自旋是固定的.

图9 二硫化钼空穴散射发射K谷声子 (a)吸收右旋光子并发射角动量为lph=−1的声子;(b)吸收左旋光子并发射角动量为lph=1的声子[19]Fig.9.K-valley phonon emitted in hole scattering of MoS2:(a)A stimulated right-handed photon is absorbed and a phonon withlph=−1 is emitted;(b)a stimulated left-handed photon is absorbed and a phonon withlph=1 is emitted[19].

如图9(a),用受激右旋光扫描样品,可以观察到在λK,v+～ωph的能量处有一个共振峰,根据选择定则,发射的手性声子在K点具有赝角动量−1.共振峰在164.4 meV(另一个198 meV的峰不明显,因为48 meV声子的极化小).对于受激左旋光子,仅观察到一个190 meV的峰,对应于40 meV的声子模,而另两个模式不会参与,因为它们在镜像操作下是相异的,这是由于在散射过程中,整个系统在镜像操作下关于x-y平面是相同的.在受声子和光子散射后,电子和空穴对位于不同的能谷,这与近来发现低能量激子具有大的动量[26]相一致.相似的,能量为1.65 eV的左旋光子激发K′点的空穴而发射K′点的手性声子.所以在确定的能谷的手性声子可以通过受激光子得到.通过二级极化光照射样品,可以产生大量有确定频率的谷声子[19].

5.5 观察手性谷声子的实验设想

5.5.1 谷声子的圆极化红外光吸收或发射

由于在能谷处位于不同能带的声子具有不同的赝角动量,可以观察谷声子(声子能带)带间散射的圆极化红外光谱.在能谷处子晶格的圆极化振动导致了非零的离子磁矩,可以直接与光子耦合,所以通过极化红外吸收或发射可以观测到谷声子.正如前面的讨论,谷声子在电子或空穴谷间散射的过程中被激发.如图10,假设位于能带ε1的能谷K′处的声子被电子大量激发,通过能量为ε2-ε1的左旋圆极化红外光子或能量为ε3-ε1右旋红外光子的激励,可以观察到相应的左旋或右旋光致发光.

如果产生大量位于能带ε2的谷声子,通过红外激励可以观察到能量为ε3-ε2或ε2-ε1左旋光致发光或能量为ε4-ε2右旋光致发光.所以由红外光谱的共振峰,可以区分谷声子.图10标注了能谷K′处声子的能带和相应的赝角动量,蓝色椭圆标记了在电子谷间散射过程中被激发的谷声子,绿线反映了所有可能参与的极化红外光吸收或发射情况[19].

图10 谷声子的圆极化红外光吸收或发射示意图Fig.10.Polarized infrared absorption or emission by valley phonons.

5.5.2 谷声子霍尔效应

在非零的贝里曲率和外加面内电场的作用下,谷电子获得反常的横向速度,大小与贝里曲率成正比[27,28],将向样品两端边界发生偏转,在样品两端可探测到谷极化电流,这就是谷电子霍尔效应.最近,已经在单层二硫化钼三极管[29]和石墨烯超晶格[30]中实验观测到了谷电子霍尔效应.正如前面的讨论,在能谷处具有确定频率的声子可以大量地产生.所以,类比谷电子霍尔效应,对于谷声子,如果贝里曲率是非零的,可以观察到存在平面内应变梯度场时的谷声子霍尔效应,这提供了观察谷声子的另一方法.

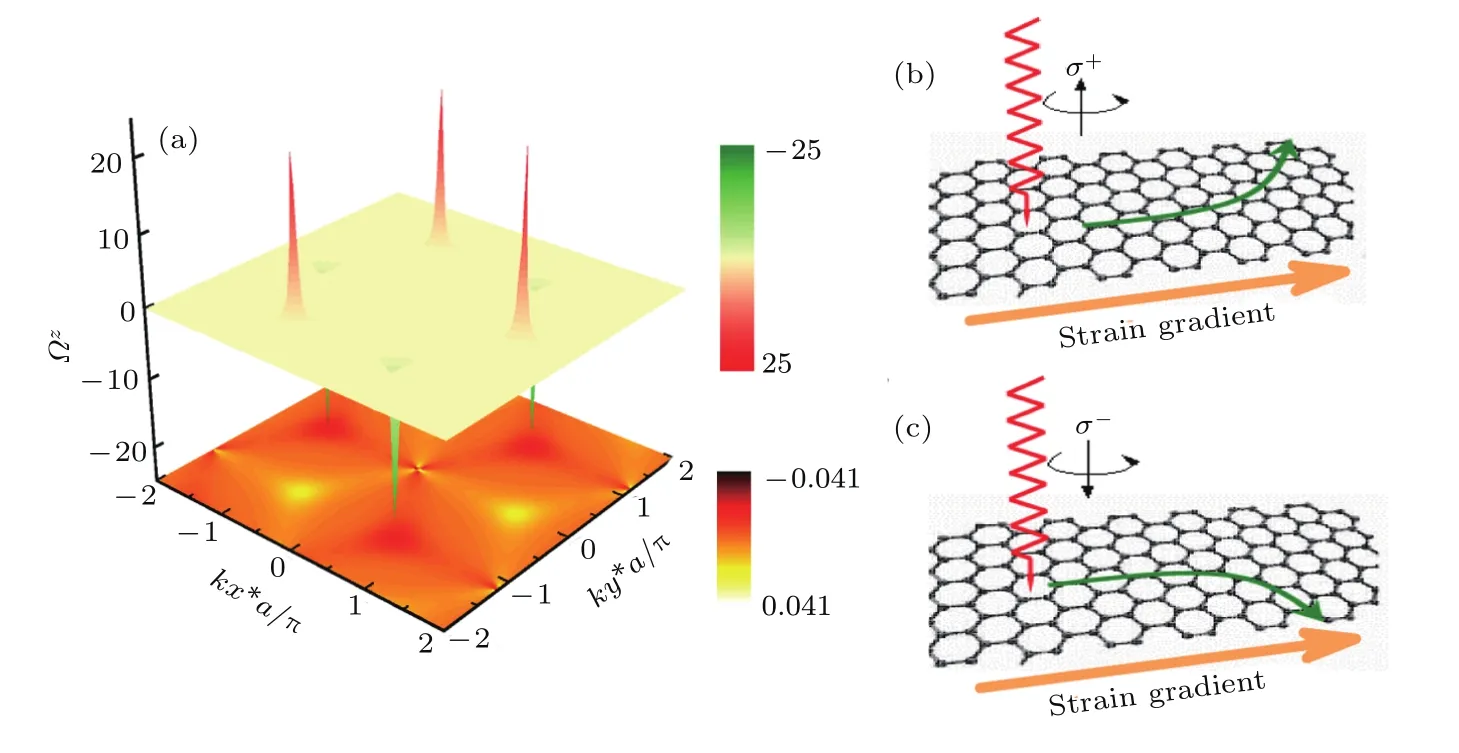
图11 六角AB晶格的声子贝里曲率和谷声子霍尔效应 (a)能带1(底部二维图)和能带2(顶部三维图)的贝里曲率;(b),(c)谷声子被右旋或左旋极化光激发(霍尔热流由红色箭头标出),在应力梯度下产生相应的声子[19]Fig.11.Phonon Berry curvature and valleyphonon Hall effect in a honeycomb of AB lattice:(a)Berry curvatureof band 1(bottom contour plot)and band 2(top 3D plot);(b),(c)schematic of the valley phonon hall effect(the Hall current denoted by the olive curve arrows)undera strain gradient(the orange arrows),where valley phononsare excited by a ray of right-handed or left-handed polarizedlight(the red wave lines)[19].

由于空间反演对称性的破坏,在能谷处观察到非零的声子贝里曲率,如图11(a).能带2和能带3在能谷处有较大的贝里曲率,而能带1和能带4的贝里曲率较小.由于非零的贝里曲率,施加沿纵向的应变梯度Estrain,类似于谷电子霍尔效应,由于反常速度正比于贝里曲率与应变梯度的叉积

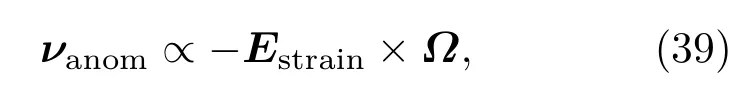
将导致在不同能谷处被左旋或右旋的极化光子激发的声子沿横向移动.如图11(b),如果光子的极性反转,则横向声子流的方向也反转.随着某一边的声子积累,可以观测到横向的温度差.如果圆极化受激光子反转,则温度差变号.已在顺磁绝缘体中观测到了声子霍尔效应,磁场改变了声子的输运,所以可以观测到横向温度差,这引发了在该领域的许多研究[31].在空间反演对称性破缺的非磁性系统中贝里曲率诱发的横向谷声子霍尔效应将带来新的应用.

6 总结与展望

本文介绍了磁性系统中声子的角动量.拉曼自旋声子相互作用是产生非零声子角动量的原因,且声子角动量是磁化强度的奇函数,这可以解释声子霍尔效应中当磁场反向时横向热流也反向的现象.除了零点能量,在绝对零度声子也具有非零的角动量.在经典极限条件下总的声子角动量消失,这是由于零点角动量与热激发下声子模的角动量相抵消.在有较大磁化强度和强自旋声子相互作用的磁性材料中不能忽视声子角动量在总角动量中的贡献.回顾爱因斯坦德哈斯效应,在计算电子的角动量时需要扣除声子角动量的部分,经过修正可以精确地确定自旋和轨道角动量.

除了在磁性系统中发现了声子角动量的存在,在非磁性六角晶格体系中的布里渊区高对称点上发现了手性声子.在这些高对称点上具有三重旋转对称性,声子模可以用赝角动量来标记.二维晶格平面内中心反演对称性破缺和在K,K′处时间反演对称性破缺是谷声子模非简并且具有确定的赝角动量的根本原因.在Γ点存在时间反演对称性,具有相反赝角动量的声子模简并.在这些高对称点上的手性声子不仅决定了电子谷内和谷间散射的选择定则而且赋予了声子学其他的潜在效应,如谷声子贝里曲率和谷声子霍尔效应.在这些高对称点的邻近区域中声子的色散关系取极值,所以具有较大的态密度.因此,手性声子在谷电子学,尤其在电子或空穴的谷内或谷间散射中扮演了重要的角色.

根据以上讨论,非简并的手性声子存在于时间反演对称性被破坏或空间反演对称性被破坏的系统中.在时间反演对称性被破坏的磁性系统中,声子携带非零角动量,这对回磁比的修正有重要的影响.在空间反演对称性被破坏的非磁性系统,布里渊区的高对称点处有手性声子,具有量子化的赝角动量,这提供了研究谷电子学的另一种方法.

声子角动量可以用于精确测定回磁比,研究自旋声子耦合、热霍尔效应等方面.北京国家重点磁学实验室的研究团队用多铁性金属有机物研究共振量子磁电耦合效应时指出,自旋-声子相互作用可以引起电介质介电常数的变化,体系声子角动量的改变很好地解释了磁化的隧穿效应[32].手性声子在电子谷内或谷间散射的选择定则、谷声子霍尔效应中扮演了重要的角色,为基于能谷的电子学和声子学的应用打下基础.来自马萨诸塞大学的研究团队联系TMDCs材料中电子光子的耦合与手性声子和电子、圆极化光子的相互作用,研究二维材料光子、电子和声子之间的耦合.对于理解凝聚态系统的基本性质具有至关重要的作用[33].来自武汉大学的研究团队在声子晶体中考虑能谷的概念,得出其重要的涡旋性质并建立了激发选择定则[34].

声子角动量以及手性声子的研究刚刚开始,相关理论和应用值得进一步的深入研究,比如晶格对称性与手性声子的内在本质联系、声子角动量和手性声子与材料磁性的依赖关系、手性声子如何影响电声子相互作用、声子角动量和手性声子的测量与应用等.由于声子在凝聚态物理中广泛存在,如超导、电声相互作用、布里渊区及拉曼散射、热电效应、热效应等,手性声子在这些领域中必将不可回避并将起到关键影响.声子角动量及手性声子的研究将会带动凝聚态物理学中与声子相关学科方向的相关探索与新的发展.

备注在此综述文章的写作完成后,《Science》杂志在2月2日发表了在二硒化钨中通过瞬态荧光测量观测手性声子实验结果[35],验证了电子或空穴谷间散射中手性声子参与的选择定则.

[1]Einstein A,de Haas W J 1915Verh.Dtsch.Phys.Ges.17 152

[2]Leduc M A 1887J.Phys.6 378

[3]Strohm C,Rikken G,Wyder P 2005Phys.Rev.Lett.95 155901

[4]Inyushkin A V,Taldenkov A N 2007JETP Lett.86 379

[5]Sheng L,Sheng D N,Ting C S 2006Phys.Rev.Lett.96 155901

[6]Kagan Y,Maksimov L A 2008Phys.Rev.Lett.100 145902

[7]Qin T,Niu Q,Shi J R 2011Phys.Rev.Lett.107 236601

[8]Zhang L 2011Ph.D.Dissertation(Singapore:National University of Singapore)

[9]Zhang L F,Niu Q 2014Phys.Rev.Lett.112 085503

[10]Ray T,Ray D K 1967Phys.Rev.164 420

[11]Ioselevich A S,Capellmann H 1995Phys.Rev.B51 11446

[12]Qin T,Zhou J,Shi J R 2012Phys.Rev.B86 104305

[13]Walton D 1967Phys.Rev.Lett.19 305

[14]Reck R A,Fry D L 1969Phys.Rev.184 492

[15]Xiao D,Yao W,Niu Q 2007Phys.Rev.Lett.99 236809

[16]Zeng H L,Cui X D 2016Wuli45 505(in Chinese)[曾华凌,崔晓冬2016物理 45 505]

[17]Zeng H L,Dai J F,Yao W,Xiao D,Cui X D 2012Nat.Nanotech.7 490

[18]Chen S Y,Zheng C X,Fuhrer M S,Yan J 2015Nano Lett.15 2526

[19]Zhang L F,Niu Q 2015Phys.Rev.Lett.115 115502

[20]Chen S Y,Wu Q,Mishra C,Kang J,Zhang H,Cho K,Cai W,Balandin A A,Ruof fR S 2012Nat.Mater.11 203

[21]Zhou S Y,Gweon G H,Fedorov A V,First P N,de Heer W A,Lee D H,Guinea F,Castro Neto A H,Lanzara A 2007Nat.Mater.6 770

[22]Kim G,Jang A R,Jeong H Y,Lee Z,Kang D J,Shin H S 2013Nano Lett.13 1834

[23]Saito R,Jorio A,Souza Filho A G,Dresselhaus G,Dresselhaus M S,Pimenta M A 2001Phys.Rev.Lett.88 027401

[24]Malarda L M,Pimentaa M A,Dresselhaus G,Dresselhaus M S 2009Phys.Rep.473 51

[25]Cao T,Wang G,Han W P,Ye H Q,Zhu C R,Shi J R,Niu Q,Tan P H,Wang E,Liu B L,Feng J 2012Nat.Commun.3 887

[26]Wu F,Qu F,MacDonald A H 2015Phys.Rev.B91 075310

[27]Chang M C,Niu Q 1996Phys.Rev.B53 7010

[28]Xiao D,Chang M C,Niu Q 2010Rev.Mod.Phys.82 1959

[29]Mak K F,McGill K L,Park J,McEuen P L 2014Science344 1489

[30]Gorbachev R V,Song S J C,Yu G L,Kretinin A V,Withers F,Cao Y,Mishchenko A,Grigorieva I V,Novoselov K S,Levitov L S,Geim A K 2014Science346 448

[31]Sheng L,Sheng D N,Ting C S 2006Phys.Rev.Lett.96 155901

[32]Tian Y,Shen S P,Cong J Z,Chai Y S,Yan L Q,Wang S G,Sun Y 2016J.Am.Chem.Soc.138 782

[33]Goldstein T,Chen S Y,Tong J,Xiao D,Ramasubramaniam A,Yan J 2016Sci.Rep.6 28024

[34]Lu J Y,Qiu C Y,Ke M Z,Liu Z Y 2016Phys.Rev.Lett.116 093901

[35]Zhu H,et al.2018Science359 6375