基于光滑约束正则化的电磁波层析反演

林芳鹏，戴前伟，雷 轶

(1.中南大学 有色金属成矿预测教育部重点实验室，长沙 410083;2.广西交通工程检测有限公司，南宁 530011；3.中南大学 地球科学与信息物理学院，长沙 410083)

0 引言

层析成像技术(Computed Tomography，CT)是反演孔间电磁波数据的主要方法之一，其分为走时层析成像和衰减层析成像[1-3]。电磁波层析成像原理基于Radon变换，即电磁波初至时或振幅可用射线经过的各单元的慢度或衰减系数的线性积分表示。射线路径与慢度或衰减系数有关，且射线覆盖角度与网格剖分大小直接影响射线长度，因此层析反演的实质是解病态方程组[4]。

正则化可以有效地解决地球物理中的不适定性问题，通过将反问题的先验信息和对解估计的预期，加入到反演计算中以消除方程病态性，从而保证计算的稳定性[4-6]。常用的正则化约束条件有3种：①最小模型约束；②最平缓模型约束；③最光滑模型约束[7-8]，笔者采用最光滑模型约束，即模型参数二阶导数最小。正则化参数的选择直接决定了正则化的有效性，常用的选择方法分为2类：①已知原始数据的误差水平时可以采用Morozov偏差原理、广义偏差原理、Arcangeli准则等方法；②不能预先估计原始数据误差水平时，拟最优准则、广义交叉检验准则、L曲线法等都是有效的方法[8-11]。由于层析反演中初至时或振幅值的误差水平都是未知的，故笔者基于L曲线法选取正则化参数。层析反演的常用算法有(反投影技术)BPT、(代数重建技术)ART、(联合迭代重建技术)SIRT、共轭梯度法(CG)、最小二乘QR分解法(LSQR)等[6,12]。因为LSQR在解大型稀疏矩阵方程组时具有节约存储空间、运算速度快的特点，所以与其他算法相比LSQR更适合解决病态问题[13]。

1 光滑约束正则化LSQR算法

层析成像求解的基本方程组为式(1)。

Gm=d

(1)

假设有n条射线，p个网格单元。G为n×p的系数矩阵，包含第ni条射线在第pj个网格单元中的射线长度；m为p×1的慢度矩阵或衰减系数矩阵；d为n×1的走时矩阵或振幅矩阵。

由于式(1)方程组具有病态性，为保证解的稳定性需要加入正则化：

‖Gm-d‖2+λ‖Dm‖2

(2)

式中：λ为正则化参数；D是光滑约束矩阵，即二阶导数型正则化。式(2)等价于解最小二乘问题：

(3)

Ax=b

(4)

因为LSQR法具有节约存储空间、计算速度快、数值稳定性好等特点，所以应用LSQR法解方程组式(4)。LSQR法遵循最小二乘的原则，在限定的解空间内寻求最佳解，它包含了Lanczos迭代和Givens正交变换两个过程，其详细的推导可参考文献[14-15]。LSQR算法过程如下：

1)初始化。

2)循环计算k=1、2、3、…重复以下步骤。

3)Lanczos双对角化。

βk+1uk+1=Avk-αkuk，

αk+1vk+1=ATuk+1-βk+1vk。

4)正交变换。

5)迭代计算。

6)收敛判别。若迭代次数达到最大值或方程组的解随迭代次数增加无明显变化时，停止迭代。

2 L曲线法

正则化参数λ的选择直接影响层析成像的精度[16]。λ过小时强调数据拟合，数据噪音可能会被放大而出现过拟合的现象；λ过大时强调光滑度而忽视了数据拟合，数据噪音被忽略而出现过抑制的现象。

L曲线法基于偏差函数‖Gm-d‖和约束项‖Dm‖在对数坐标上的平面曲线，该方法通过求解(lg‖Gm-d‖，lg‖Dm‖)曲线的最大曲率点(拐角点)来确定最佳正则化参数[17-18]。求取最大曲率点的推导公式如下，令：ρ=lg‖Gm-d‖，η=lg‖Dm‖，那么正则化参数λ对应的点的曲率为：

(5)

其中：ρ'、ρ''、η'、η''分别表示ρ、η的一阶和二阶导数，且均是正则化参数λ的函数。式(5)最大值对应的正则化参数λ即为最佳正则化参数，此时的L曲线拐点是偏差函数和约束项的最佳平衡点。

3 计算实例

3.1 简单模型

图1为简单模型示意图，模型为5 m×10 m，背景的相对介电常数为20；异常体边长为1 m，相对介电常数为6。数据采集为单发多收模式，发射天线置于X=0 m，垂直移动间隔为0.5 m；接收天线置于X=5 m，垂直移动间隔为0.25 m。计算实例均基于走时层析成像，采用直线射线路径计算系数矩阵G，利用能量比法提取电磁波初至时。

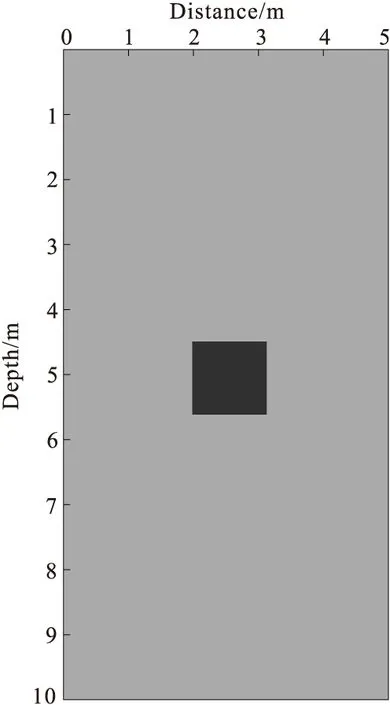
图1 简单模型图Fig.1 Simple model

图2 简单模型正则化参数的L曲线Fig.2 L-curve for computing the optimal regularization parameter in simple model

正则化参数λ选用0.01、0.05、0.5、1、2、5、10，代入正则化目标函数中得到7组不同的层析反演结果。求取每个正则化参数对应的偏差函数值lg‖Gm-d‖和约束项lg‖Dm‖，利用三次样条拟合得到L曲线(如图2)，拐点处正则化参数λ=0.5。

如图3列举了正则化参数λ为0.05、0.5、5时的三组层析反演结果，由图3可知，不同的正则化参数得到的反演结果有明显差别。图3(a)为正则化参数λ=0.05时的电磁波速度剖面图，由于正则化参数选取过小，背景电磁波速度出现波动，且异常体的特征反映较为模糊；图3(b)为最佳正则化参数λ=0.5时的电磁波速度剖面，从图中可清晰识别异常体的位置和大小，异常体的高速特性也得以准确体现；图3(c)为正则化参数λ=5时的电磁波速度剖面，当正则化参数选取过大时，高速异常区过于光滑，导致层析成像失真。

3.2 断层模型

图4为断层模型示意图，模型为5 m×10 m，背景的相对介电常数为15；异常体的相对介电常数为25。数据采集以及反演参数设置同上。

正则化参数λ选用0.25、0.5、1、2、4、8、16，代入正则化目标函数中得到7组不同的层析反演结果，其对应的L曲线如图5所示，拐点处正则化参数λ=8。

图6为正则化参数λ为2、8、16时的三组层析反演结果。图6(a)为正则化参数λ=2时的电磁波速度剖面图，由于正则化参数选取过小，方程组的解稳定性较差，导致反演结果与实际模型误差较大；图6(b)为最佳正则化参数λ=8时的电磁波速度剖面图，从图6(b)中可清晰识别低速断层的倾向、大小和位置；图6(c)为正则化参数λ=16时的电磁波剖面图，当正则化参数选取过大时，断层异常区过于圆滑、数据拟合较差，导致难以从图像中识别异常体特征。

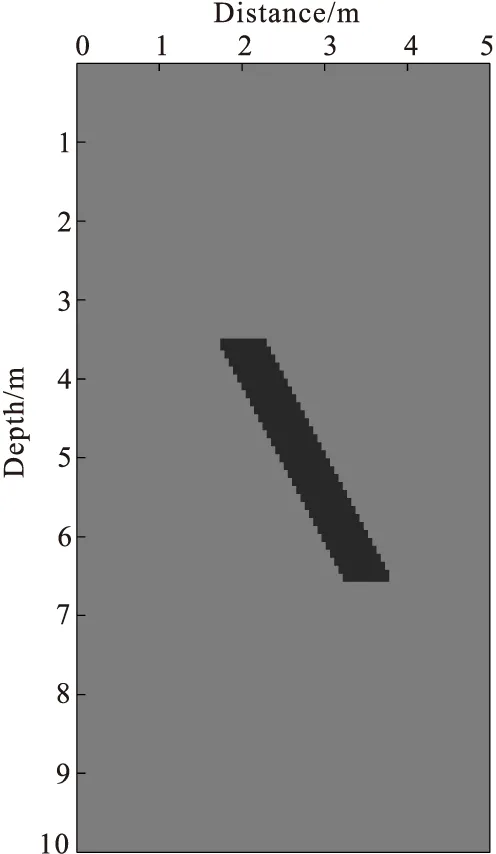
图4 断层模型Fig.4 Fault model

图5 断层模型正则化参数L曲线Fig.5 L-curve for computing the optimal regularization parameter in fault model

图6 断层模型的层析反演剖面图Fig.6 The results of tomography inversion in fault model(a) λ=2；(b) λ=8；(c) λ=16

4 总结

笔者提出了基于光滑约束正则化的LSQR层析反演算法，介绍了L曲线法选取最佳正则化参数。由简单模型和断层模型的走时层析成像结果可知：①基于光滑约束正则化的LSQR算法适用于层析成像计算，它具有稳定性和高效性；②利用L曲线的拐点可准确选择最佳正则化参数，其对应的速度剖面图能清晰反映异常体的特征。

层析成像的影响因素有多种，需要指出，本文中直线射线路径以及射线覆盖程度都会造成一定程度的误差，导致电磁波速度剖面中异常体的位置、大小与实际模型有所不同。

参考文献：

[1] 赵连锋，朱介寿，严忠琼，等．岩溶勘察层析成像试验：成像效果分析[J]．物探化探计算技术，2002，24(4)：332-336．

ZHAO L F, ZHU J S, YAN Z Q, et al. A test of tomography in the cavern survey: imaging effect analysis [J]. Computing Techniques for Geophysical and Geochemical Exploration, 2002, 24(4):332-336. (In Chinese)

[2] 冯锐．电磁波层析成象[J]．地震学报，1997，19(5)：524 - 534．

FENG R.Electromagnetic wave tomography[J]. Journal of seismic，1997, 19(5):524-534. (In Chinese)

[3] 陈昌彦，沈小克，苏兆锋，等．电磁波层析成像技术在复杂地质边坡工程勘察中的应用研究[J]．地球物理学进展，2012，27(2)：796-803．

CHEN C Y, SHEN X K, SHU Z F, et al. Application of electromagnetic wave tomography on geotechnical investigation of the complex geological slope engineering [J]. Progress in Geophysics, 2012, 27(2): 796-803. (In Chinese)

[4] 成谷, 张宝金, 马在田，等. 浅谈反射地震走时层析中的正则化[J]. 地球物理学进展, 2007, 22(6):1715-1721.

CHENG G, ZHANG J B, MA Z T, et al. Regularization in traveltime tomography for reflection seismic data [J]. Progress in Geophysics, 2007, 22(6): 1715-1721. (In Chinese)

[5] 董一飞, 张致付. 正则化方法在无线电波层析中的应用[J]. CT理论与应用研究, 2016, 25(3):287-298.

DONG Y F, ZHANG Z F. Application of regularization method in radio wave tomography [J]. CT Theory and Applications, 2016, 25(3): 287-298. (In Chinese)

[6] 杨文采. 地球物理反演和反射地震走时层析成像[M].北京:地质出版社, 1989.

YANG W C. Geophysical inversion and seismic tomography [M] Beijing: Geological Publishing House , 1989. (In Chinese)

[7] 柳建新，童孝忠，郭荣文，等. 大地电磁测深勘探：资料处理反演与解释[M]. 北京：科学出版社，2012.

LIU J X, TONG X Z, GUO R W, et al. Magnetotelluric sounding: data inversion and interpretation [M]. Beijing: Science Press, 2012. (In Chinese)

[8] 张文权, 翁爱华. 地面核磁共振正则化反演方法研究[J]. 吉林大学学报(地球科学版), 2007, 37(4):809-813.

ZHANG W Q, WENG A H. On regularization inversion method of surface nuclear magnetic resonance data [J]. Journal of Jilin University (Earth Science Edition), 2007, 37(4): 809-813. (In Chinese)

[9] 王化祥, 何永勃, 朱学明，等. 基于L曲线法的电容层析成像正则化参数优化[J]. 天津大学学报(自然科学与工程技术版), 2006, 39(3):306-309.

WANG H X, HE Y B, ZHU X M, et al. Regularization Parameter optimum of electrical capacitance tomography based on L-curve method [J]. Journal of Tianjin University, 2006, 39(3):306-309. (In Chinese)

[10] 冯德山, 王珣. 大地电磁双二次插值FEM正演及最小二乘正则化联合反演[J]. 中国有色金属学报, 2013(9):2524-2531.

FENG D S, WANG X. Magnetotelluric finite element method forward based on biquadratic interpolation and least squares regularization joint inversion [J]. The Chinese Journey of Nonferrous Metals, 2013, 23(9): 2524-2531. (In Chinese)

[11] 马涛, 陈龙伟, 吴美平,等. 基于L曲线法的位场向下延拓正则化参数选择[J]. 地球物理学进展, 2013, 28(5):2485-2494.

MA T, CHEN L W, WU M P, et al. The selection of regularization parameter in downward continuation of potential field based on L-curve method[J]. Progress in Geophysics, 2013, 28(5): 2485-2494. (In Chinese)

[12] 杨薇, 刘四新, 冯彦谦. 跨孔层析成像LSQR算法研究[J]. 物探与化探, 2008, 32(2):199-202.

YANG W, LIU S X, FENG Y Q, et al. A study of the LSQR algorithm for cross-hole tomography [J]. Geophysical and Geochemical Exploration, 2008, 32(2):199-202. (In Chinese)

[13] 刘劲松, 刘福田, 刘俊,等. 地震层析成像LSQR算法的并行化[J]. 地球物理学报, 2006, 49(2):540-545.

LIU J S, LIU F T, LIU J, et al. Parallel LSQR algorithms used in seismic tomography [J]. Chinese Journal of Geophysics, 2006 , 49(2): 540-545.(In Chinese)

[14] PAIGE C C, SAUNDERS M A. LSQR: An algorithm for sparse linear equations and sparse least squares[J]. Acm Transactions on Mathematical Software, 1982, 8(1):43-71.

[15] 张东, 乔友峰, 姜麟舜,等. 地震层析成像中LSQR算法的快速求解[J]. 物探化探计算技术, 2011, 33(6):632-635.

ZHANG D, QIAO Y F, JIANG L Y, et al. The fast algorithm of LSQR in seismic tomography [J]. Computing Techniques for Geophysical and Geochemical Exploration, 2011, 33(6):632-635. (In Chinese)

[16] 冉利民, 刘四新, 李玉喜,等. 影响跨孔雷达层析成像效果的几个因素[J]. 吉林大学学报(地球科学版), 2013, 43(5):1672-1680.

RAN L M, LIU S X, LI Y X, et al. Several factor affecting cross-hole tomography [J]. Journal of Jilin University (Earth Science Edition), 2013, 43(5):1672-1680. (In Chinese)

[17] HANSEN P C. Analysis of discrete Ill-posed problems by means of the L-curve [J]. Siam Review, 1992, 34(4):561-580.

[18] HANSEN P C, O'LEARY D P. The use of the L-curve in the regularization of discrete ill-posed problems[J]. Siam Journal on Scientific Computing, 1993, 14(6):1487-1503.