一种模糊最小二乘孪生支持向量回归机的改进算法

唐辉军 杨志民

1(宁波大红鹰学院信息工程学院 浙江 宁波 315175) 2(浙江工业大学之江学院 浙江 杭州 310024)

0 引 言

在回归过程中，数据孤立点和噪声的存在影响了回归函数的泛化能力，模糊函数通过对不同的训练数据点设置不同的隶属度以解决数据不同特性问题[1-2]。孪生支持向量回归机[3](TSVR)是一种常被使用加快数据集训练速度的有效方法。它是支持向量机的扩展，运算速度是普通支持向量机的4倍。结合上述两者，相关学者提出模糊孪生支持向量机(FTSVR)模型[4]，其对一定训练速度和噪声要求下的数据集训练过程起到了良好的优化作用。最小二乘孪生支持向量回归机(LSTSVR)综合了最小二乘和孪生支持向量机的特性，它在训练点两侧生成一对不平行的函数，进而确定回归函数的上下界。通过实验发现，基于TSVR的最小二乘孪生支持向量机(LSTSVR)相比TSVR有更出色的性能[5]，模糊最小二乘孪生支持向量机[6-7](FLSTSVR)表现为LSTSVR的模糊特性，具备一定的计算优势和可行性。

本文在构建FLSTSVR基本数学模型的基础上对其进行优化改进。考虑结构风险最小化原则，加入L2正则化项以优化回归误差。以提高大规模高维数据集计算效率为目标，应用L1范数和增量学习方法优化数据训练过程，改进模型在相关数据集上得到了验证。

1 FLSTSVR

考虑回归训练集T={(x1,y1),(x2,y2),…,(xl,yl)}，其中xi∈Rn表示输入，yi∈Rn则表示相应的输出。线性情况下的模糊最小二乘支持向量机寻求两个不平行的函数：

f1(x)=w(1)x+b(1)f2(x)=w(2)x+b(2)

(1)

根据相关概念知识，f1(x)、f2(x)由以下相关数学模型所构造：

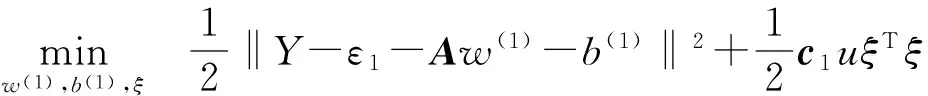
(2)

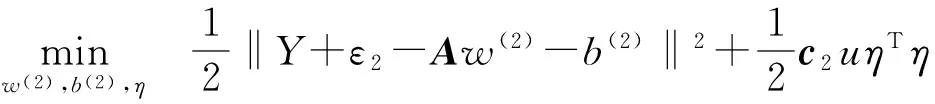
(3)

c1、c2表示惩罚参数向量，A=[x1,x2,…,xl]T，u表示了模糊隶属度，ξ、η表示了相应的松弛变量。对式(2)(即求解f1(x))进行方程求解，消去松弛变量ξ，再由得到的目标函数L分别为w(1),b(1)求偏导，得到：

(4)

进行化简后，得到结果为：

(5)

式中：G=[Ae],f1=Y-ε1。

同理可对式(3)进行偏导求解，进而求得w(2)、b(2)。在非线性情况下，可应用一定的核函数变换构建相关模型[8-9]，相关模型表现为：

s.t.Y-(K(A,A)w(1)+b(1))=ε1-ξ

(6)

s.t. (K(A,A)w(2)+b(2))-Y=ε2-η

(7)

按照线性模型求解的思路，可化简求得式(6)结果为：

(8)

式中：H=[K(A,A)e],f=Y-ε1。基于其良好的构建特性，FLSTSVR在一定数据集中取得了良好的模型训练和验证结果。

2 模糊函数的设定

从数据点的位置定义来看，模糊函数的设定依据样本分布状况而形成。在线性模式下，设定样本数据点离中心的距离与最大距离的比值为一类常用的设定方法[10-11]。表现为：

(9)

式中：xr为样本中心点，λ为相应的一个常数值。l为样本数量。xi(i=1,2,…,l)为样本中的个体。当样本为非线性分布时，在基于文献[12-13]的基础上，选择一个包含样本数据的最小半径超球作为依据，并且根据样本点升维后与超球心之间的距离与半径的比值作为模糊隶属度可更好地揭示其模糊效果。设置模糊函数为：

(10)

式中：K(x)为选取的核函数，a为超小球球心，R为样本空间半径，ε、λ为数值较小的常数值，依据不同的计算要求，可采用不同的模糊函数。

3 FLSTSVR 的L2 、L1范数改进

式(2)和式(3)考虑了经验风险，为了保证其最小化且同时降低VC维，这里引入结构风险最小化概念进行模式改进，从而使得模型在整个数据样本集中的期望风险得到控制。基于结构风险最小化原则，L2正则项被认为能够有效地防止过拟合，从而提升模型的泛化能力。考虑线性模型式(2)、式(3)下的L2范数改进，其基本结构模型为：

s.t.Y-(Aw(1)+b(1))=ε1-ξ,ξ=[ξ1,ξ2,…,ξl]

(11)

s.t. (Aw(2)+b(2))-Y=ε2-ηiη=[η1,η2,…,ηl]

(12)

以式(11)中为例，其表示了在式(2)和式(3)的最后加入一个L2正则项以期达到训练误差和测试误差最小[14]。基于式(11)的模型，按照式(4)的计算过程分别对相关参数求偏导，可得到：

(13)

经过变量消解化简计算，可得到结果：

(14)

参数γ表现为一定的较小数值，以保证逆矩阵的可求解性，按照同样的方法，也可求得模型式(12)的计算结果w(2)、b(2)。

当训练样本规模大且维度高的时候，前述模型的构建过程中存在着大量的计算，在求解相关矩阵的过程中可能耗费大量的时间。L1范数被认为是具备稀疏特性选择的主要工具，对前述模糊最小二乘支持向量机进行L1范数改进以应对大规模数据计算，改进线性模型式(2)和式(3)为：

γ‖w(1)‖

s.t.Y-(Aw(1)+b(1))=ε1-ξ,ξ=[ξ1,ξ2,…,ξl]

(15)

γ‖w(2)‖

s.t. (Aw(2)+b(2))-Y=ε2-ηiη=[η1,η2,…,ηl]

(16)

在文献[15]的参考基础上，令：

(17)

基于模型式(15)，按照前述方法对相关变量进行偏导数求解，得到：

(18)

化简得到：

w(1)=w+-w-=-2(ATA)-1γe

(19)

求得w(1)后代入式(18)，可得到b(1)的值，进而求得最后的结果。同理基于相同的方法，w(2)、b(2)也可相应的求得。非线性模型式(6)、式(7)的L2、L1范数改进则基本上与线性模型雷同，最大的区别表现为替换线性模型中的样本空间A为K(A,A),K为选取的核函数。

4 FLSTSVR增量学习模型

如前所述，当遇到大规模数据集训练时，虽可借助于L1范数求解最优化问题，但由于原始矩阵A的庞大可能导致计算效率低下，支持向量机增量学习模型并非一次性导入全部样本进行计算。而是充分选择具有代表性的样本进行周期迭代学习，然后原始问题就可解析为一系列的子问题求解以减少大规模数据迭代计算。实验表明，增量支持向量机(ISVM)[16-18]在一些数据集上可以在保证精度的同时可以减少训练时间。

基于ISVM特性，提出一种基于距离选择的模糊最小二乘孪生支持向量机模型(IS-FLSTSVR)。由于孤立点和噪声的少量特性和偏离中心性，确保最大量的有效样本被选入迭代过程中。其基本运算流程如下：

(1) 初始化：对于T={(x1,y1),(x2,y2),…,(xl,yl)}，划分样本集为n份(支持向量个数一般不超过总数量10%)，随机选择某一份数据集作为初始训练集IX，其他作为增量数据集UX。

(2) 训练模型：选取式(11)和式(12)或式(15)和式(16)作为增量模糊最小二乘支持向量机的训练模型，得到基于目前数据训练集的边界支持向量集SV1。

(3) 增量循环迭代训练：判断UX是否为空，若成立则训练终止，否则选择下一个增量数据集。对其中的每一点，计算其与支持向量的距离，若距离小于参数值ε，则将其从增量数据集中删除，否则将其作为新样本点与原先的支持向量样本点SV1进入IX，得到新的支持向量SV2。欧几里德距离、名氏距离、角度距离公式可被选做计算距离公式的一种。

(20)

(4) 支持向量选择：对SV2中的支持向量进行更新选择，为防止过拟合，继续采用式(20)中的原先选取的距离公式，对两两支持向量样本点进行距离计算，若两个支持向量距离小于上述参数阈值，则将随机从SV2 中删除一个。否则保留其中支持向量集中参与下一次训练，令SV1=SV2。

(5) 终止训练：判断UX中是否有新的样本点，若有则转(3)，否则训练终止。

(6) 输出结果：采用SV2中的结果作为边界支持向量，形成最后增量学习结果。

5 实 验

为验证改进方法有效性，对TSVR、LSTSVR、L2-FLSTSVR、L1-FLSTSVR、IS-FLSTSVR进行了相关实验运算和数值验证分析。所有实验在都在Intel(R)Core(TM)i5-2450MCPU，4 GB内存和MATLAB r2011b的环境中进行，ε=1.0E-3，采用均方根误差(RMSE)±标准差(STD)的方法作为计算结果损失对比。选取式(8)为模糊函数，基于标准UCI小规模数据集，线性模式下算法对比结果见表1。

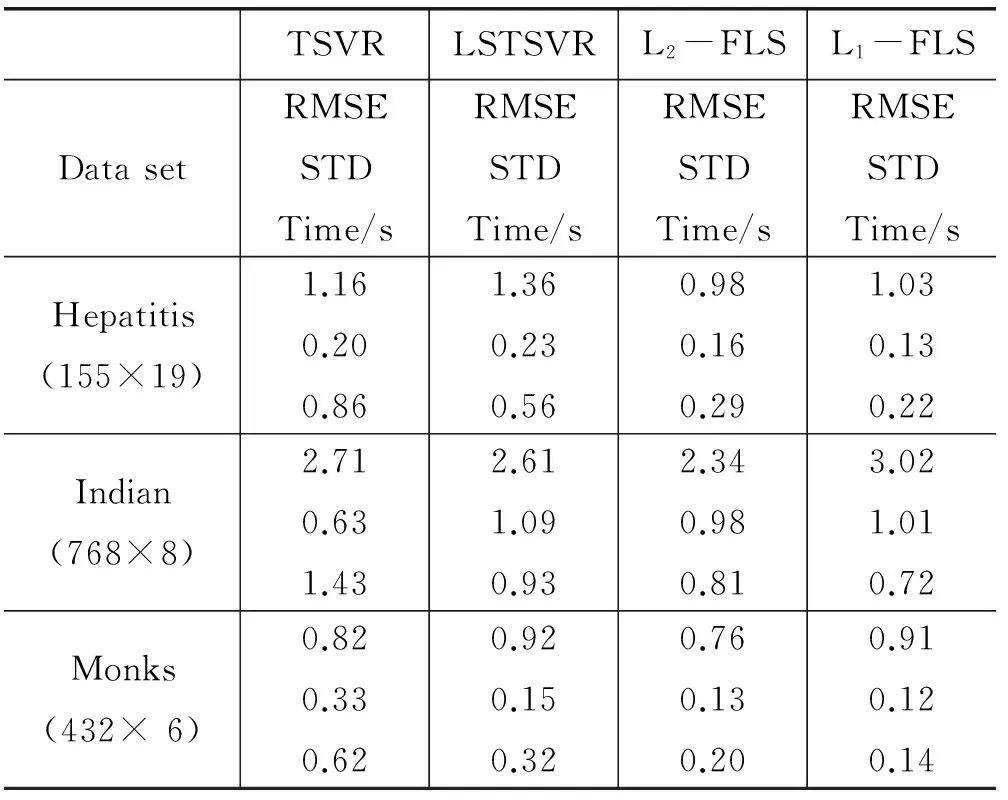
表1 FLSTSVR线性模型结果比较

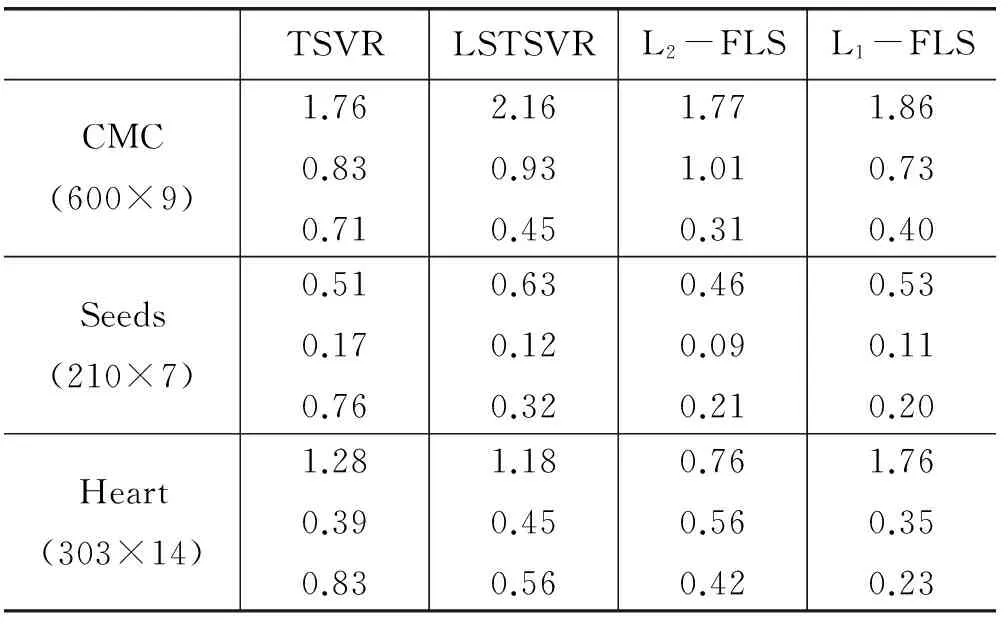
续表1

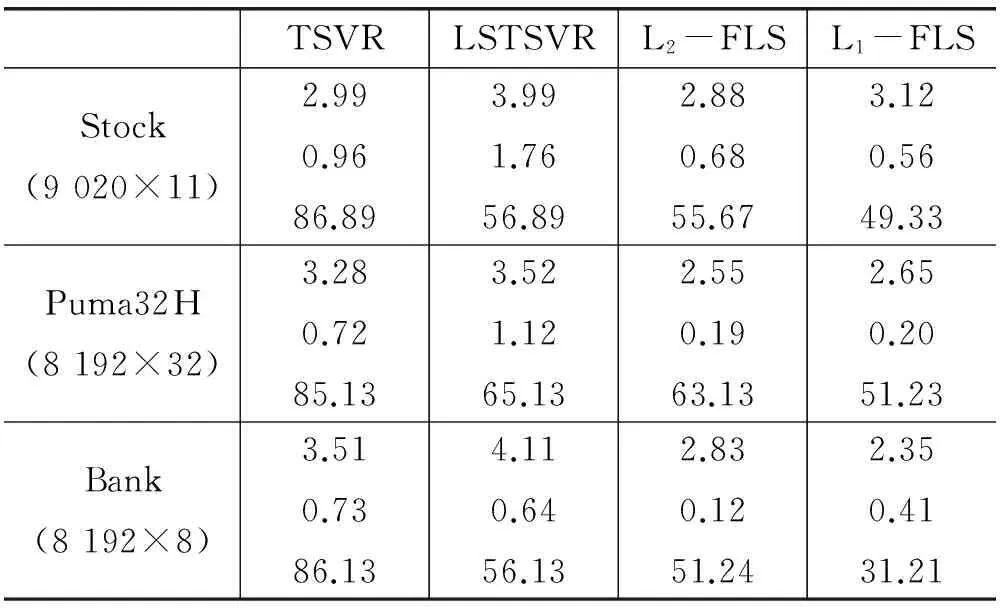
其中L2-FLS、L1-FLS分别对应了L2-FLSTSVR、L1-FLSTSVR算法。从表1中可以看出，在大多数数据集中L2-FLSTSVR从计算精度上表现出了更好的性能，运算时间也表现的较好。L1-FLSTSVR相比其他算法结果有一定的差距，但计算时间能够得到保证。

表2关注非线性情况下相关算法的计算表现，选取高斯核函数作为变换函数。其中，表1和表2中的RMSE和STD数值与实际运算时间相比放大了100倍。从表2的计算结果来看，L2-FLSTSVR 运算时间并非最优但计算误差领先于其他算法，L1-FLSTSVR相对计算速度更好，但计算精度并不理想。LSTSVR在时间上好于TSVR，但两者与L2-FLSTSVR相比，在计算精度有明显差距。

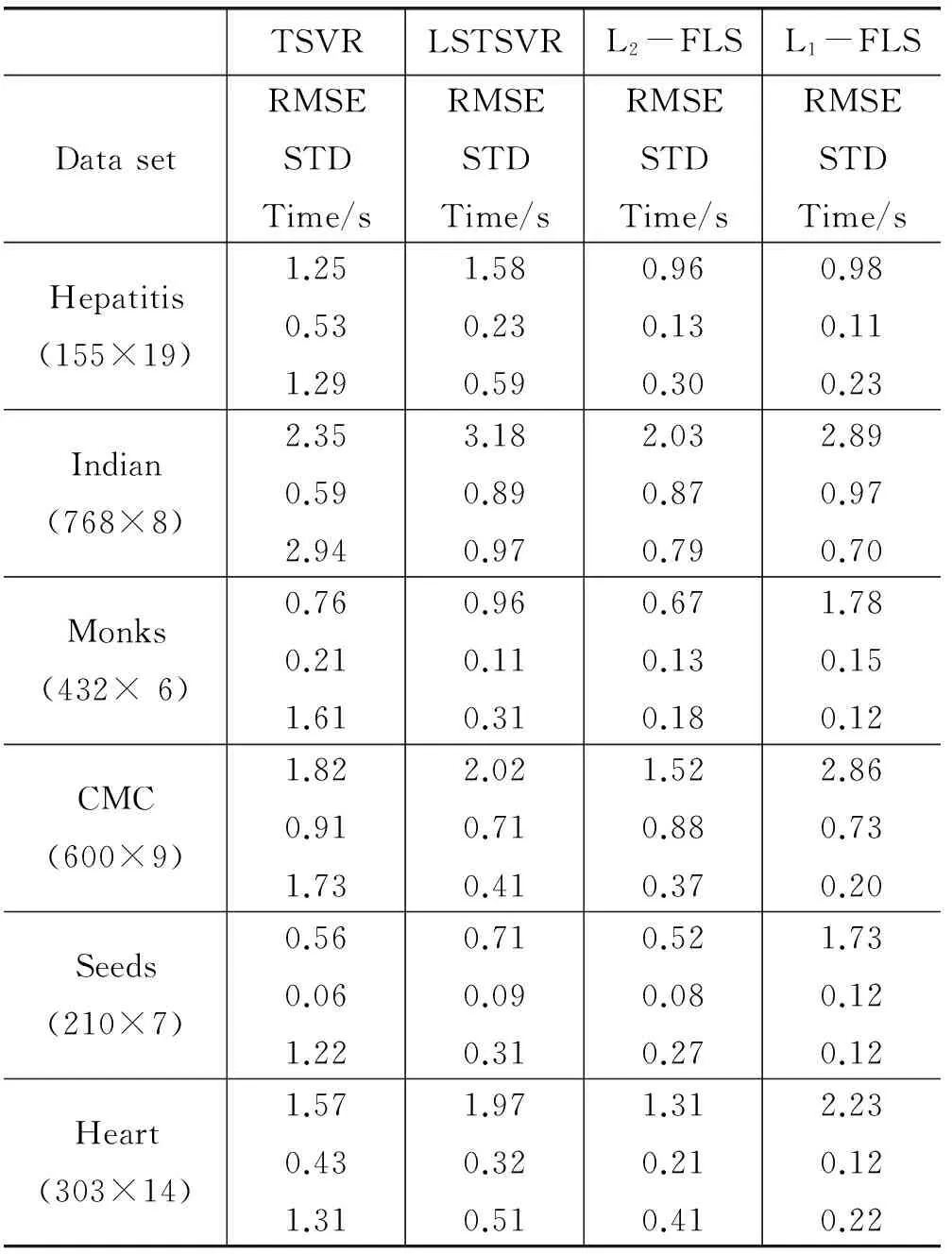
表2 FLSTSVR非线性模型结果比较

TSVR在运算时间上与其他算法有较大差距，为了更好地展现相关算法在噪声环境下的运算效率与表现，选取Sinc 函数在区间的回归结果作为验证对象。基于噪声函数随机产生50个噪声点，选择LSTSVR、L1-FLSTSVR、L2-FLSTSVR算法作为实验算法。其中噪声设置函数ei=(0.5-|xi|/2π)，xi服从均匀随机分布。图1表示无噪声数据的Sinc函数的回归结果，图2则显示有噪声情况下的回归结果。L2-FLSTSVR拟合的曲线过程表现出了较好的泛化性能，曲线几乎不受噪声影响。

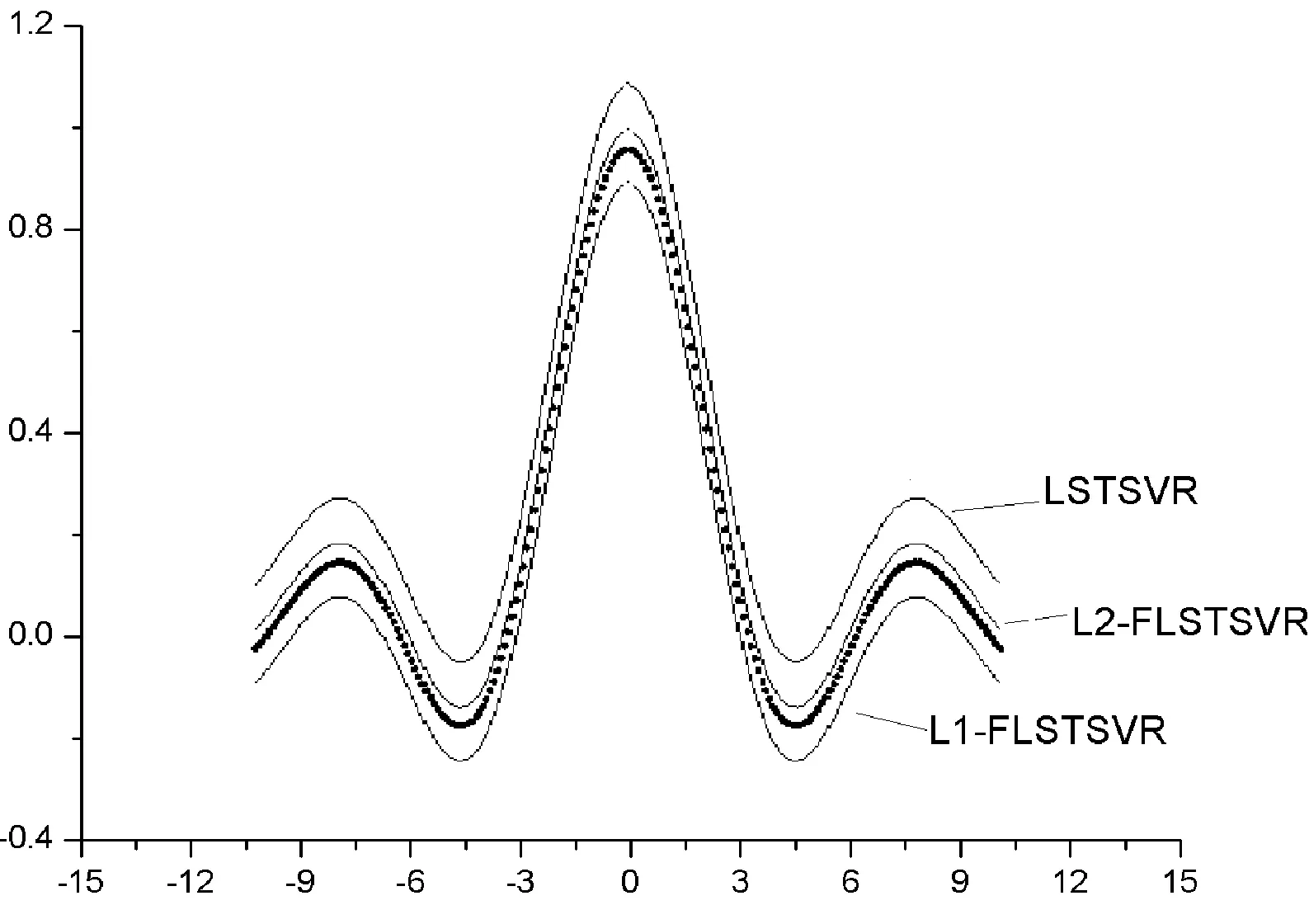
图1 无噪声情况下作用于Sinc函数回归结果

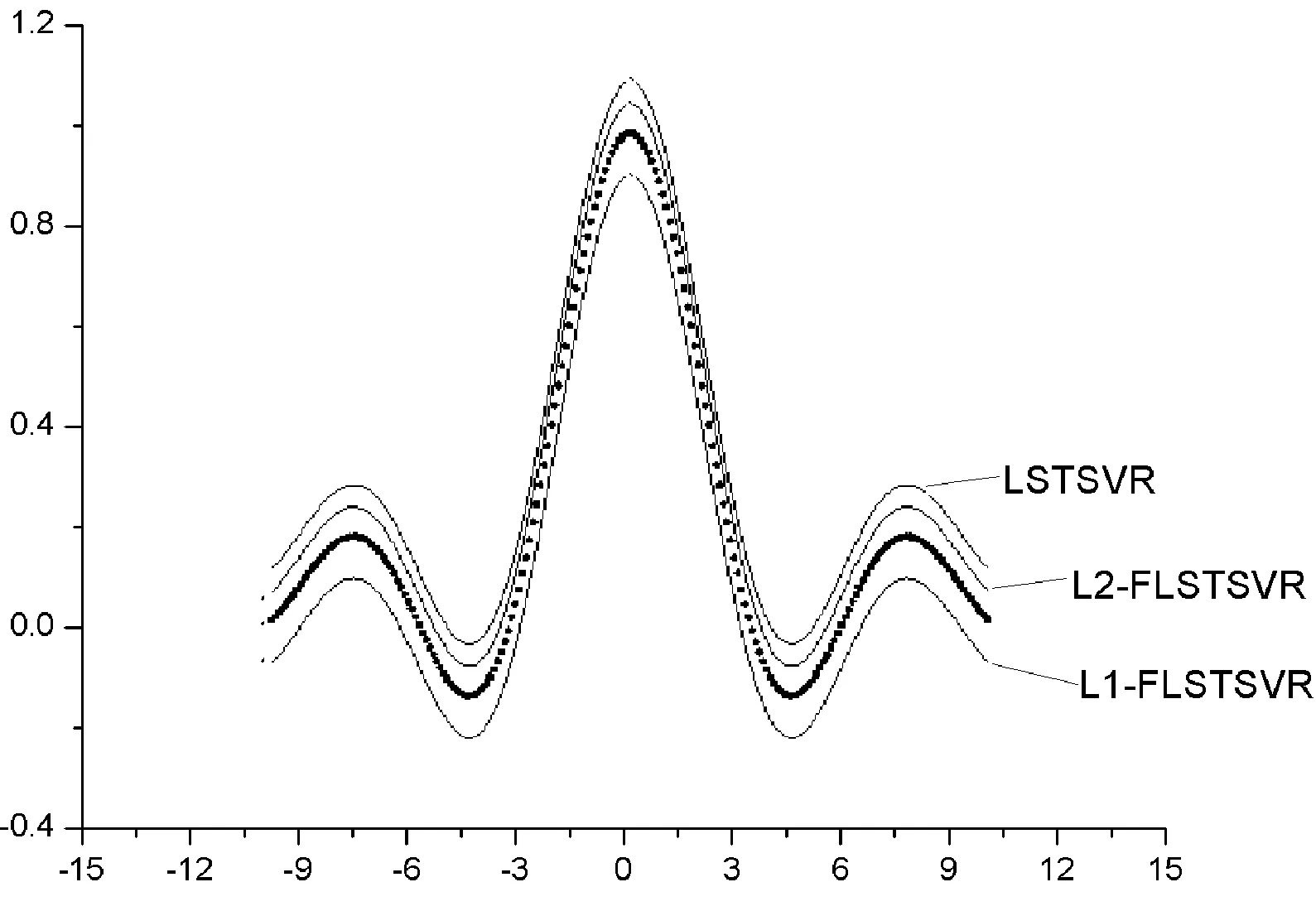
图2 有噪声情况下作用于Sinc函数回归结果

为了验证相关算法在大数据集中的良好应用结果，采用高斯核函数开展非线性数据结构实验对比计算，相关结果见表3。可以看出，L1-FLSTSVR在计算时间上有显著的效果，并且在不同数据集上取得的精度相对较好，领先于TSVR和LSTSVR。

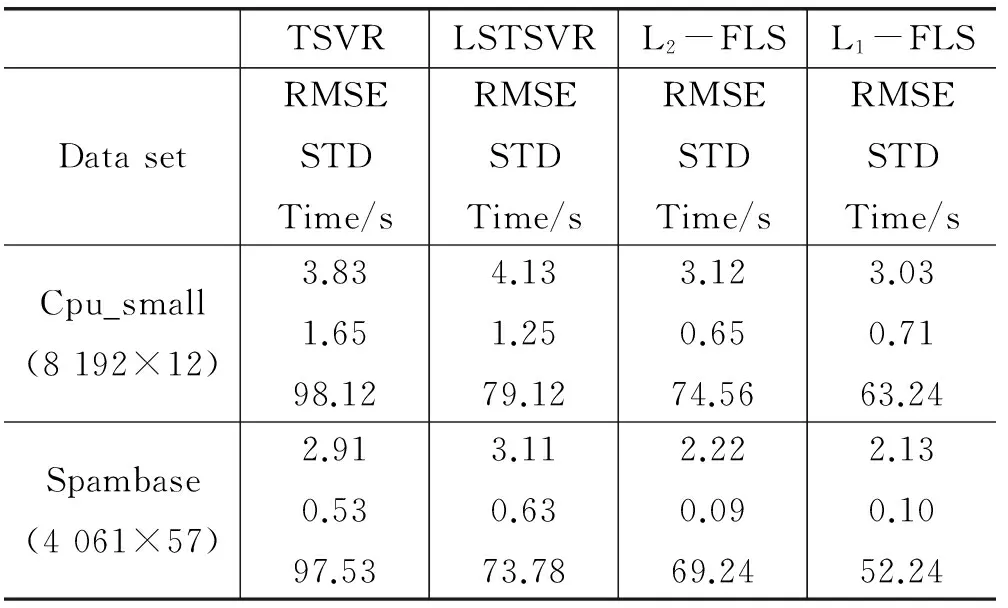
表3 大规模数据集下的运算结果

续表3

从表1-表3中可以看出，L2-FLSTSVR、L1-FLSTSVR在不同规模数据集下可以取得良好计算效果。考虑大规模数据集下其增量计算模式，结果如表4所示。

表4 大规模数据集下的运算结果

表4中L2-IS，L1-IS分别表示了L2-FLSTSVR、L1-FLSTSVR算法的增量学习模式，距离公式采用了式(20)中的角度距离公式A-Distance。从表4中可以看出，增量学习计算方法的时间效用得到了很好的体现，L1-IS在大多数数据集上的计算精度也处于领先地位。考虑式(20)提供的三种距离公式类型，应用L1-IS算法对相同的数据集进行增量选择运算，相关结果见表5。从表5可以看出，基于角度距离公式(A-Distance)的方法相对其他两类算法确实取得了较好的结果。为进一步验证其优越性，对于Sinc函数的500个数据均匀样本点，设定样本选择过程为5个部分，输出相应的训练数据的误差。实验过程数据误差可以见图3。在计算过程中可以得知，A-Distance从起点到终点的数据误差是最小的，再次说明角度距离增量学习方法具备较好的计算特性。

表5 不同距离公式下的IS-FLSTSVR运算结果

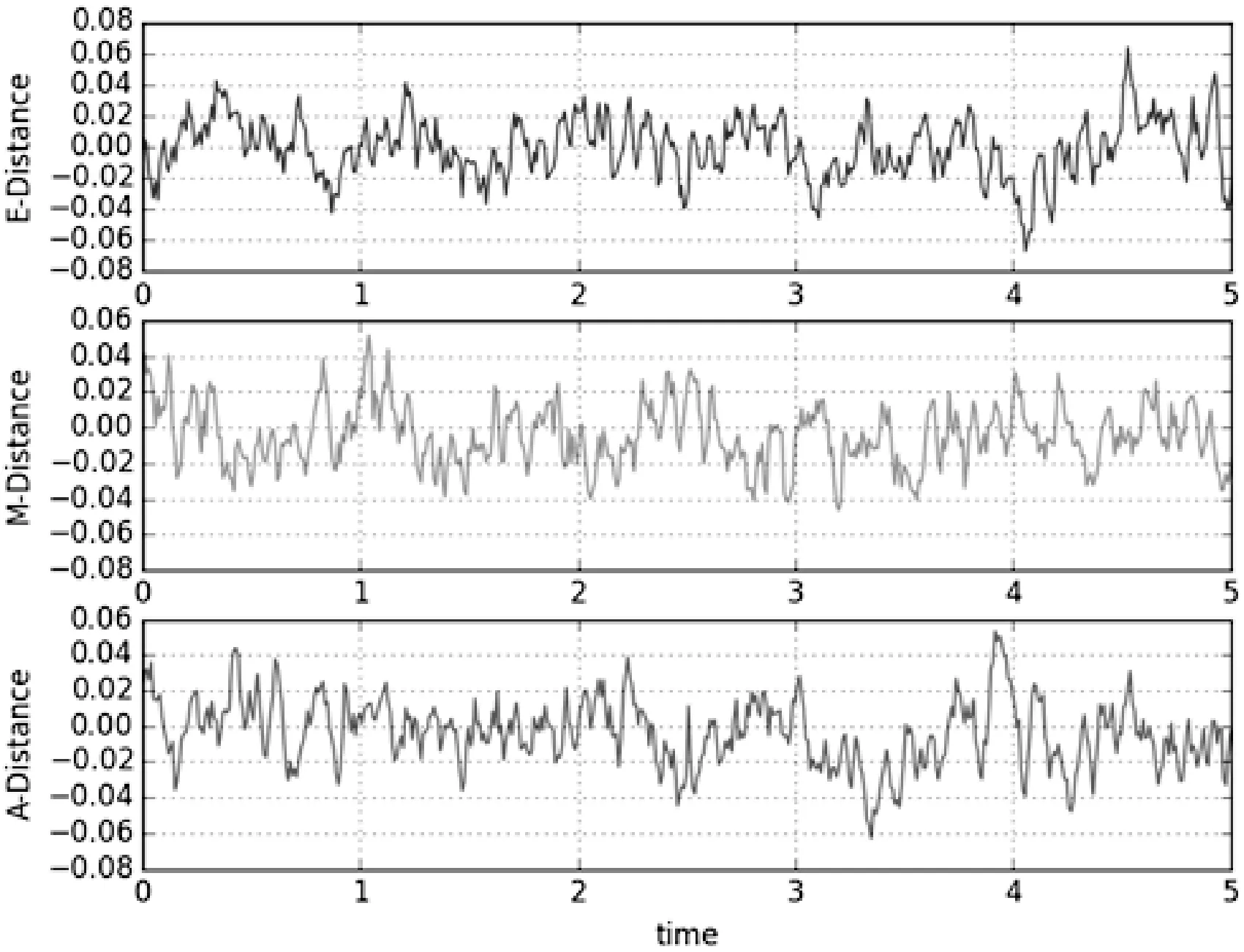
图3 不同距离公式下的Sinc函数增量学习

6 结 语

基于回归过程，在构建模糊最小二乘孪生支持向量机模型的基础上，对其进行了有效改进。通过不同范数的作用，使得模型的泛化性能和鲁棒性更好。在基于训练速度的要求上，应用了增量学习方式对模糊最小二乘孪生支持向量机模型进行了训练集迭代选择。相关实验证明，改进方法可在一定数据集上提高运算效率，提升精度误差。未来将在参数选择变化和在更广泛数据集选择上开展理论和实验应用研究，使得相关模型更具效用。

[1] Han P H,Liu Y H.Fuzzy Support Vector Machines for Pattern Recognition and Data Mining[J].international journal of fuzzy systems,2002,4(3):826-834.

[2] Li Kai,Ma Hongyan.A Fuzzy Twin Support Vector Machine Algorithm[J].International Journal of Application or Innovation in Engineering & Management,2013,2(3):459-462.

[3] Peng Xinjun.TSVR:an efficient Twin Support Vector Machine for regression[J].Neural Networks,2010,23(3):365-372.

[4] Xu Yitian,Wang Laisheng.A weighted twin support vector regression[J].Knowledge-Based Systems,2012,33(3):92-101.

[5] Shao Y H,Zhang C H,Yang Z M,et al.An ε-twin support vector machine for regression[J].Neural Computing & Applications,2013,23(1):175-185.

[6] Xu Yitian,Xi W,Lv X,et al.An improved least squares Twin Support Vector Machine[J].Journal of Information & Computational Science,2012,9(4):1063-1071.

[7] Xu Yitian,Lv X,Wang Z,et al.A Weighted Least Squares Twin Support Vector Machine[J].Journal of Information Science & Engineering,2014,30(6):1773-1787.

[8] Lin C F,Wang S D.Fuzzy support vector machines[J].IEEE Transactions on Neural Networks,2002,13(2):464-471.

[9] Lu Cunlou,Gao Shangbing,Zhou Zecheng.Maize Disease Recognition via Fuzzy Least Square Support Vector Machine[J].Journal of Information and Computing Science,2013,8(4):316-320.

[10] 黄华娟.孪生支持向量机关键问题的研究[D].中国矿业大学,2014.

[11] Li J,Cao Y,Wang Y,et al.Binary classification with noise via fuzzy weighted least squares twin support vector machine[C]//Control and Decision Conference.IEEE,2015:1817-1821.

[12] Hao P Y.Fuzzy one-class support vector machines[J].Fuzzy Sets & Systems,2008,159(18):2317-2336.

[13] 吴青,刘三阳,杜喆.回归型模糊最小二乘支持向量机[J].西安电子科技大学学报,2007,34(5):773-775.

[14] Shao Y H,Zhang C H,Wang X B,et al.Improvements on twin support vector machines[J].IEEE Transactions on Neural Networks,2011,22(6):962-968.

[15] 梁锦锦,吴德.稀疏L1范数最小二乘支持向量机[J].计算机工程与设计,2014,35(1):294-297.

[16] Ping S.Incremental Learning with Support Vector Machines[C]//IEEE International Conference on Data Mining.IEEE Computer Society,2001:641-642.

[17] Domeniconi C,Gunopulos D.Incremental Support Vector Machine Construction[C]//IEEE International Conference on Data Mining.IEEE Computer Society,2001:589-592.

[18] 蒋尔雄.数值逼近[M].上海:复旦大学出版社,2007.