利率对我国股市波动性影响的实证研究

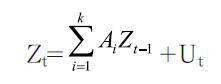
【摘要】本文选取上海银行间同业拆放利率（Shibor）和沪深300指数收盘价的时间序列数据，运用ADF检验、协整检验、Granger因果检验、建立VAR模型等实证研究利率对股市的影响，格兰杰因果检验的结果表明利率是股市收益率的格兰杰原因。通过建立VAR模型，本文发现利率变动与股市收益率整体上呈负相关关系，且VAR回归方程通过显著性检验。实证研究结果表明：利率与股市收益率存在反向变动的趋势，且利率对股市波动性的影响显著。

【关键词】利率 股市收益率 VAR模型

一、研究思路

本文选取了2015年1月5日至2016年11月16日Shibor隔夜利率与沪深300指数收盘价日数据进行实证研究，利用VAR模型、Granger因果检验、脉冲响应函数分析以及方差分解，实证分析了利率对我国股市收益率波动性的影响。

二、实证分析

（一）样本选取与数据处理

1.股市收益率数据的选取与处理。本文选用2015年1月5日至2016年11月16日间沪深300指数收盘价（文中用zs表示）的日数据作为股票收益率的样本数据，共计488个数据，数据来源于东方财富Choice数据。股市收益率通常用股票价格指数的自然对数的差分来表示，其计算表达式为：

r=ln（pt）-ln（pt-1）

其中，tp表示第t期的股票价格指数。

2.利率数据的选取与处理。本文在根据基准利率的选取原则，采用2015年1月5日至2016年11月16日上海银行间同业拆放利率（Shibor）隔夜拆借利率（文中用ll表示）数据来作为基准利率进行研究分析，样本数据共计488个样本数据，数据来源于Shibor官方网站，数据处理软件为Eviews9.0。

为了消除时间序列的异方差问题，对上海银行间同业拆放利率（Shibor）隔夜拆借利率（文中用ll表示）的原始数据取自然对数，记为lnll。

（二）实证分析过程

1.平稳性检验。

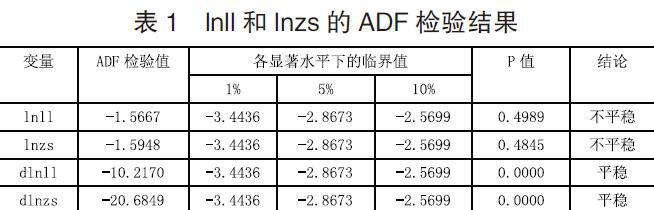
本文首先对沪深300指数收盘价的日数据序列和上海银行间同业拆放利率（Shibor）隔夜拆借利率序列进行平稳性检验。本文采用ADF检验时间序列的平稳性。对利率变量lnll进行ADF检验，检验结果（表1），显示ADF检验统计量在10%的显著水平下大于临界值，不能拒绝有单位根的原假设，这说明lnll是不平稳的时间序列，对lnll进行一次差分后得到一个新的时间序列dlnll，再对时间序列dlnll进行ADF检验，检验结果（表1），显示ADF检验统计量在1%的显著水平下小于临界值，拒绝有单位根的原假设，这说明dlnll是平稳的时间序列，因此lnll是一阶平稳时间序列。同样，对股市变量lnzs进行ADF检验，发现lnzs也是一阶平稳时间序列，检验结果如表1所示。结果表明：lnll和lnzs均为一阶单整。因此，我们先对非平稳的数据序列进行协整检验，再建立VAR模型研究变量间的关系。

2.协整检验。根据LR统计量、FPE预测误差以及AIC信息准则，最优滞后期应该为4；然而根据SC信息准则和HQ信息准则，最优滞后期应该为2。由于SC信息准则着重于构建一个更经典的模型，所以我们一般以AIC信息准则为准，而且为了使得模型中变量多些更有说服力，综合以上考虑，最终确定最优滞后期为4。

trace统计量给出的协整关系个数的检验结果显示，两组非平稳時间序列lnll和lnzs都在5%的显著性水平下存在2个协整方程，所以变量间存在2个稳定长期均衡关系。VAR模型是建立在变量间存在协整关系的基础之上的，通过证明，可以建立VAR模型。

3.向量自回归（VAR）模型。VAR模型是一种非结构化的多方程模型，它利用模型中的当期变量对当期变量的若干个滞后变量的回归来构建方程。VAR模型是把所有变量都看成是内生变量，每个方程的解释变量都是所有被解释变量的若干期滞后值所进行的回归。VAR模型的一般形式如下：

Zt=■+Ut

其中，Zt是第t期变量值构成的n维列向量；Ai表示n×n系数矩阵；k为滞后阶数；Ut则是随机误差项构成的n×1矩阵；ui为白噪声过程。

为研究利率对我国股市波动性的影响，对经自然对数调整并进行一次差分后的平稳时间序列dlnll和dlnzs建立4阶滞后期的VAR模型如下：

dlnll=0.3114dlnll（-1）+0.1701dlnll（-2）+0.0860dlnll（-3）+0.0692dlnll（-4）-0.0033dlnzs（-1）+0.0535dlnzs（-2）+0.0429dlnzs（-3）-0.0082dlnzs（-4）-0.0001.

R2=0.2478 AIC=-5.5704 SC=-5.4925

dlnzs=-0.1454dlnll（-1）+0.0297dlnll（-2）+0.0243dlnll（-3）-0.0842dlnll（-4）+0.0613dlnzs（-1）-0.0985dlnzs（-2）-0.0230dlnzs（-3）+0.1142dlnzs（-4）-0.0002.

R2=0.0479 AIC=-4.9622 SC=-4.8843

4.VAR模型稳定性检验。模型稳定性检验一般采用AR根图表检验，本文建立的VAR模型所有AR根模的倒数都小于1，位于单位圆内，说明建立的VAR模型是稳定的。

5.Granger因果检验。通过检验可以得到利率与股市收益率之间的因果关系，原假设dlnll不是dlnzs的Granger原因的概率为0.0463，小于0.05，因此可以拒绝原假设，所以dlnll是dlnzs的Granger原因；原假设dlnzs不是dlnll的Granger原因的概率为0.3293，大于0.05，因此不能拒绝原假设，所以dlnzs不是dlnll的Granger原因。即在5%的显著水平下，利率是股市收益率的Granger原因，而股市收益率不是利率的Granger原因，这表明利率可以对股票价格产生影响。

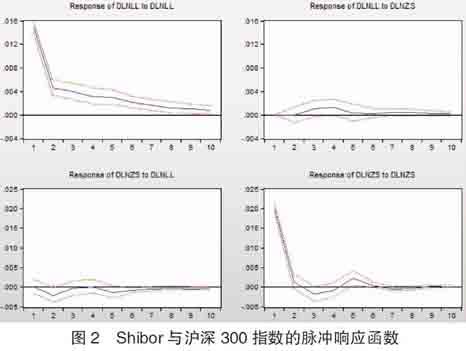
6.脉冲响应函数分析。

从图2可以看出，给利率一个负的冲击，股市收益率滞后半期出现负向的响应，但响应较小，这种负向的响应一直持续到第7期为0；而利率对来自股市收益率的冲击几乎没有响应。由此可以得出结论：利率变动与股市收益率整体上呈负相关。

7.方差分解。方差分解结果中可以看出，dlnll对dlnzs的贡献率在2%左右，dlnzs对dlnll的贡献率几乎为0。该分析结果进一步表明，利率变动会影响股市收益率，但利率变动对股市收益率的影响的贡献度很小，这与之前的Granger因果检验和脉冲响应函数分析结果一致。

三、结论

根据格兰杰因果检验，表明利率为股市收益率的格兰杰原因。说明央行调控存贷款基准利率使得市场利率发生变化，进而可以对股票价格产生影响。通过VAR模型的建立，我们得出利率变动与股市收益率整体上呈负相关，但利率变动对股市收益率的影响的贡献度很小。实证分析结果表明：利率与股市收益率存在反向变动的趋势，且VAR回归方程通过显著性检验，即利率对股市波动性的影响显著。

四、政策建议

推动货币市场和股票市场的有效联动，加快货币市场与资本市场良性关系的形成；加快各层次资本市场发展，进一步完善股票市场；进一步完善利率市场化机制，提高利率变化对股市的传导效应。

参考文献

[1]李春霞，孙笑笑.利率变动对中国股市的影响[J].经济，2016（7）：25.

[2]董维佳等.短期利率对中国股市的非对称影响[J].经济与管理研究，2016，37（6）：74-80.

[3]胡一博.基于TVP-VAR模型的利率变动与股市波动的时变关系研究[J].管理现代化，2016，36（1）：7-9.

[4]周寰宇，周开国.SHIBOR对我国股指期货市场有影响吗？——基于股指期货和SHIBOR关联性的视角[J].经济学报，2016（1）.

[5]时光，高珂.对SHIBOR作为我国货币市场基准利率的有效性检验[J].财经科学，2012（2）：20-28.

作者简介：陈浩苗（1994-），男，汉族，湖北襄阳人，四川大学经济学院硕士研究生，研究方向：金融分析。