基于移相全桥ZVS软开关的大功率变换器设计

郭双权， 李颖峰

(陕西理工大学 电气工程学院， 陕西 汉中 723000)

随着现代电力电子器件的发展，应用在通信、军工及日常生活中的大功率开关电源需求量越来越大。由于应用环境的特殊性，使得人们对开关电源数量和功率等级不断提出新的要求。目前采用开关电源并联技术，以提高较大的输出电流，而此时需要较多体积小的开关电源模块并联，既增加了成本，又增大了体积，同时也降低了电源系统的可靠性。因此，需要开发大容量大输出电流的新型开关电源产品来解决上述问题。移相全桥软开关变换器是最常用的中大功率DC-DC变换电路拓扑之一，以其开关损耗小、效率高、实现简单和高可靠性等优点，广泛应用于中大功率开关电源模块中。

本文首先对移相全桥软开关拓扑进行研究，接着推导移向全桥电路小信号模型，设计内环电流环和外环电压环的双闭环变换器控制系统，最后通过仿真试验和实验测试验证该方案的正确性。

1 移相全桥软开关电路工作原理

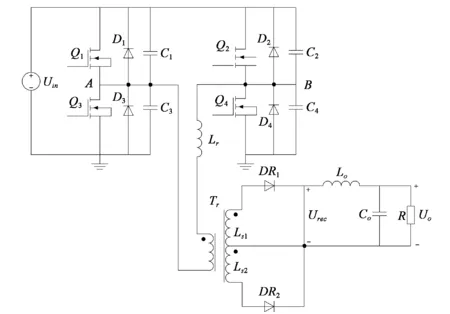
图1 移相全桥变换器主电路拓扑

移相全桥变换器主电路基本拓扑如图1所示，其中：Q1—Q4为功率开关管，D1—D4为4个功率开关管的反并联二极管，C1—C4为功率开关管的寄生电容与外部并联电容之和，Lr为谐振电感，包括变压器Tr漏感，有时也仅用变压器漏感作为谐振电感。Q1和Q3为一组桥臂，Q2与Q4为另一组桥臂，同一组桥臂的功率开关管以180°互补导通，两个桥臂导通角相差一个移相角，通过调节移相角的大小来调节输出电压。在导通时间上，Q1超前Q2，Q3超前Q4，因此我们习惯性称Q1和Q3组成的桥臂为超前臂，Q2和Q4组成的桥臂为滞后臂。Lo和Co为输出滤波电感和电容。主电路中功率开关管的漏源极两端并联的电容为Ci(i=1,2,3,4)，Ci可限制功率开关管两端电压不突变，从而实现功率开关管的零电压关断。同理，在主电路中增加谐振电感Lr，Lr可抽走将要开通的功率开关管并联电容Ci上的电荷，同时给同一桥臂上的另一个功率开关管上并联的电容Ci充电，从而实现功率开关管零电压开通。

移相全桥变换器主电路工作波形与驱动波形如图2所示，图中IP为变压器的初级电流，UAB为输入变压器一次侧的电压，电路工作过程如下[1-2]：

(1)在t0时刻以前，Q1和Q4导通，直流母线电压经变压器后使整流二极管DR1导通向负载提供能量；在t0时刻Q1关断，IP给C1充电，且C3同时放电。由于并联电容C1和C3存在，使得Q1是零电压关断。

(2)在t1时刻，C3电压放电至零，Q3反并联二极管自然导通，为零电压开通Q3创造条件。

(3)在t2时刻，关断Q4，IP给C4充电，且C2同时放电，由于并联电容C2和C4存在，使得Q4是零电压关断，且UAB电压由零变为负值，整流二极管DR2导通，此时整流二极管DR1和DR2同时导通，使输出电压为零，造成原边绕组电压也为零，输入电压全部加在谐振电感Lr上，因此这段时间Lr和C2、C4在谐振工作。

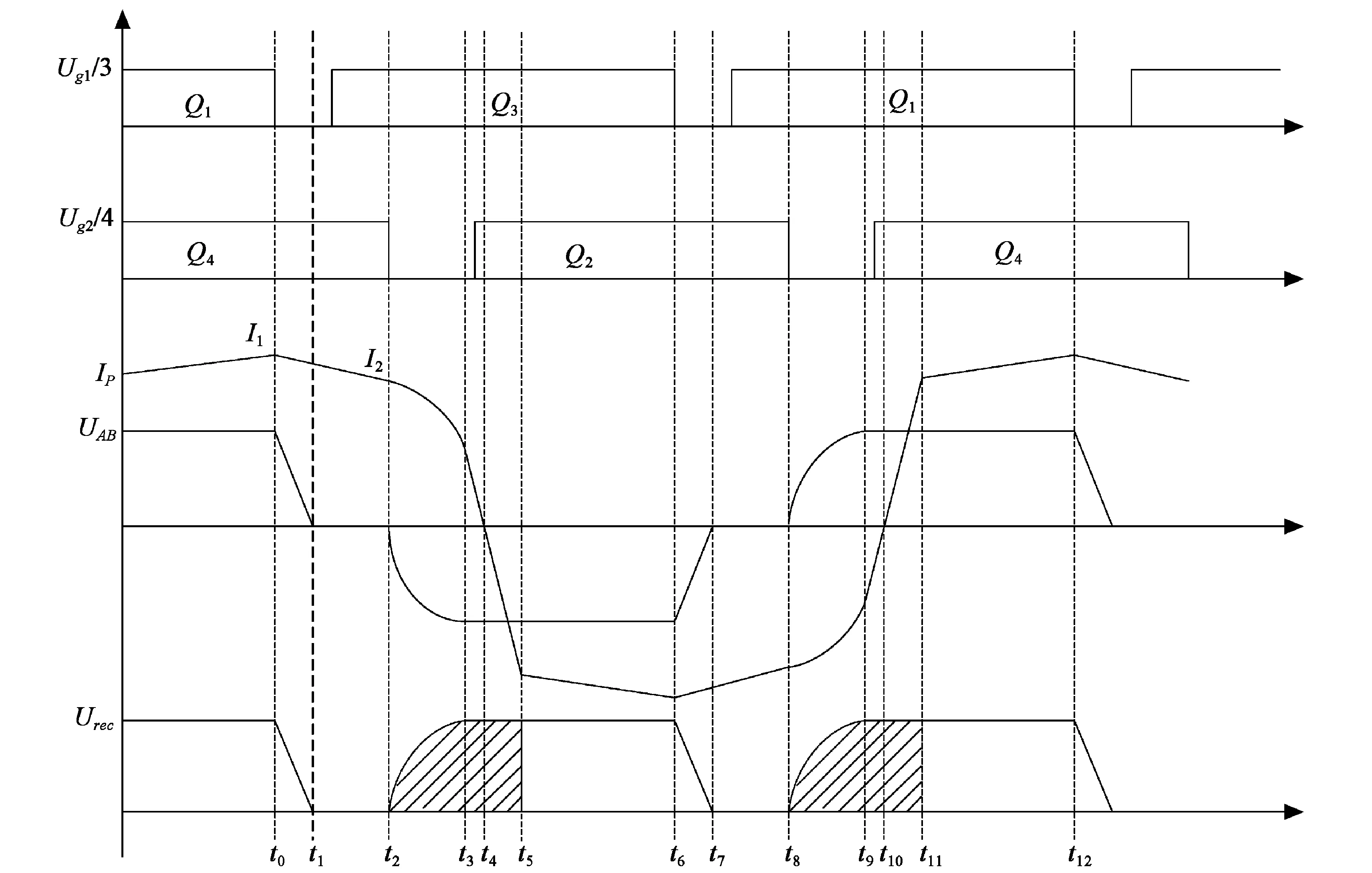
图2 移相全桥变换器主电路工作波形

(4)在t3时刻，C4电压等于输入电压，使得Q2反并联二极管自然导通，为零电压开通Q2创造条件。由于整流二极管DR1和DR2同时导通，使输出电压为零，因此原边绕组电压也为零，进而使IP电流线性下降。

(5)在t4时刻，IP电流下降为零，Q2和Q3反并联二极管自然关断，Q2和Q3有电流流过，但是由于IP负方向增长不足以向负载提供电流，所以变压器原、副变电压为零，由于输入电压作用使IP负方向线性增长，直至整流二极管DR1关断为止。

(6)在t5时刻，原边电流线性增加，使得DR1关断，DR2导通，向负载进行功率传输。

(7)在t6时刻，Q3关断，变换器开始下半个周期转换，其工作过程与上半个周期类似。

2 变换器系统结构组成及参数设计

2.1 变换器系统结构组成

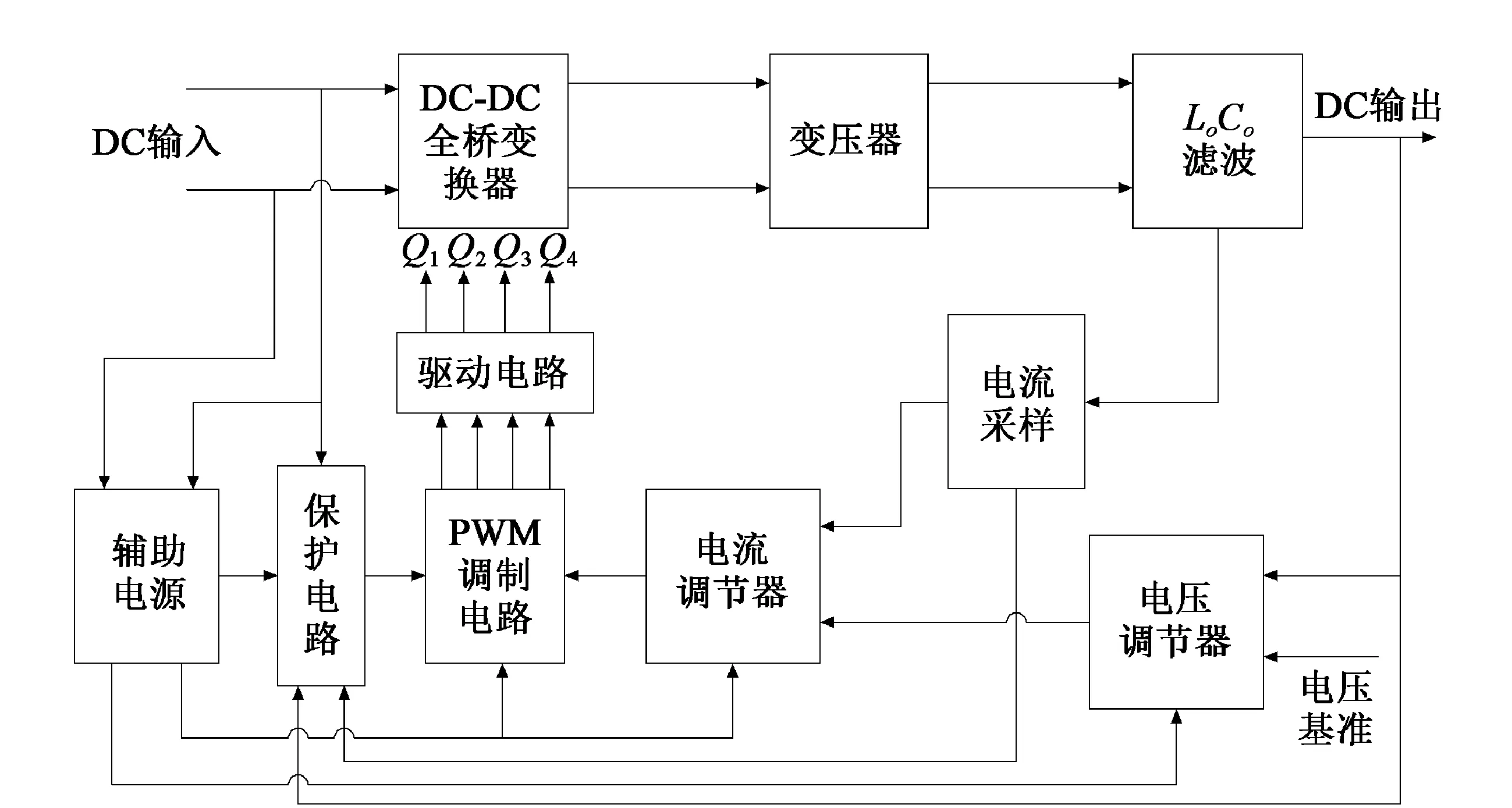
图3 移相全桥软开关变换器结构图

图3为基于移相全桥软开关拓扑的变换器结构图。变换器系统主要由主电路、整流滤波电路、PWM控制电路、辅助电源供电电路、隔离驱动电路及保护电路组成。其主电路选用移相全桥拓扑结构，移相控制方式采用模拟芯片实现，通过控制移相角使变换器输出电压维持在恒定的48 V。移相全桥电路控制功率开关管的通断，使得直流母线高压经变压器后转换成低电压交流方波；PWM控制电路采用电流内环和电压外环的双闭环控制策略[3]，且电流环采用峰值电流控制[4]，反馈电压和基准电压进行比较，然后经过PI调节器作为电流内环的给定值，此给定值与输出滤波电感电流比较后经PI调节器输出，并与三角载波信号一起控制驱动信号移相角的大小，从而实现输出电压恒定。辅助电源电路将直流母线电压转化成±15 V DC、±12 V DC和+5 V DC，为隔离驱动电路、PWM控制电路、保护电路、模拟运放器和电流霍尔传感器供电。保护电路对输入过压、输出过流及输出过压等情形进行保护。

2.2 器件选型和关键参数设计

课题拟定的开关频率f=100 kHz，最大输出功率Po=2.4 kW，满载效率拟定为η=94%，求得输入功率Pin=Po/η=2.55 kW，因输入电压Uin范围为400～420 V，求得输入电流有效值范围为6.07～6.375 A。在选取MOSFET功率开关管时，一般取大于2倍的耐压和电流应力余量，同时兼顾滞后桥臂的软开关特性，最终选取Infineon公司的CoolMOS管SPW55N80C3，额定耐压850 V，额定电流54.9 A，TO-247封装。在最大占空比和最低输入电压条件下，设计高频变压器变比，使输出电压能够达到输出电压要求。本文输出电压Uo为48 V，输出整流二极管选取ST公司的肖特基二极管STPS60SM200CW，其导通压降UD=0.64 V，输出滤波电感的压降ULo=0.4 V，副边最大占空比Deff(max)=0.85，Uo(max)=50 V为最大输出电压，计算得到副边输出电压最小值为

(1)

在输入电压Uin(min)=400 V时，计算变压器原副边匝比为

(2)

谐振电感设计时需考虑占空比丢失和轻载时能实现滞后桥臂的零电压开关，I为滞后桥臂关断时一次电流大小，功率开关管SPW55N80C3的输出电容Coss=305 pF，应满足

(3)

课题设计的电源输出满载电流为50 A，其谐振电感设计按照大于0.7倍满载电流实现零电压开关设计，输出电流最大值Io(max)=55 A，滤波电感电流ΔiLo/2脉动量为10%的最大电流，则计算一次电流I大小为

(4)

联立式(3)和式(4)，求得谐振电感Lr=3.29 μH。

3 变换器建模及双闭环控制系统设计

3.1 移相全桥变换器建模

从本质上分析，移相全桥电路属于Buck电路，对Buck电路运用状态空间平均法，并引入扰动量求其小信号模型，图4所示为Buck变换器小信号模型。而移相全桥电路较Buck电路多了一个占空比丢失状态[5]，因此移相全桥电路小信号模型异于Buck电路。在移相全桥变换器中，变压器副边有效占空比Deff=D-ΔD，占空比D由控制信号决定其大小，ΔD为占空比损失，参照文献[6]求ΔD的计算公式：

(5)

式中f为开关频率，Uin、Uo分别为输入和输出电压，IL为输出滤波电感电流，n为变压器副边与原边的匝数比，n=1/N。由式(5)可知，Uin、IL及占空比D都影响移相全桥电路的有效占空比Deff，于是得到有效占空比的扰动量表达式为

(6)

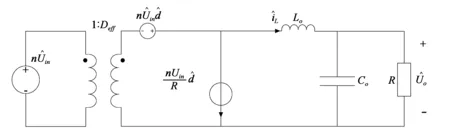
图4 Buck变换器小信号模型

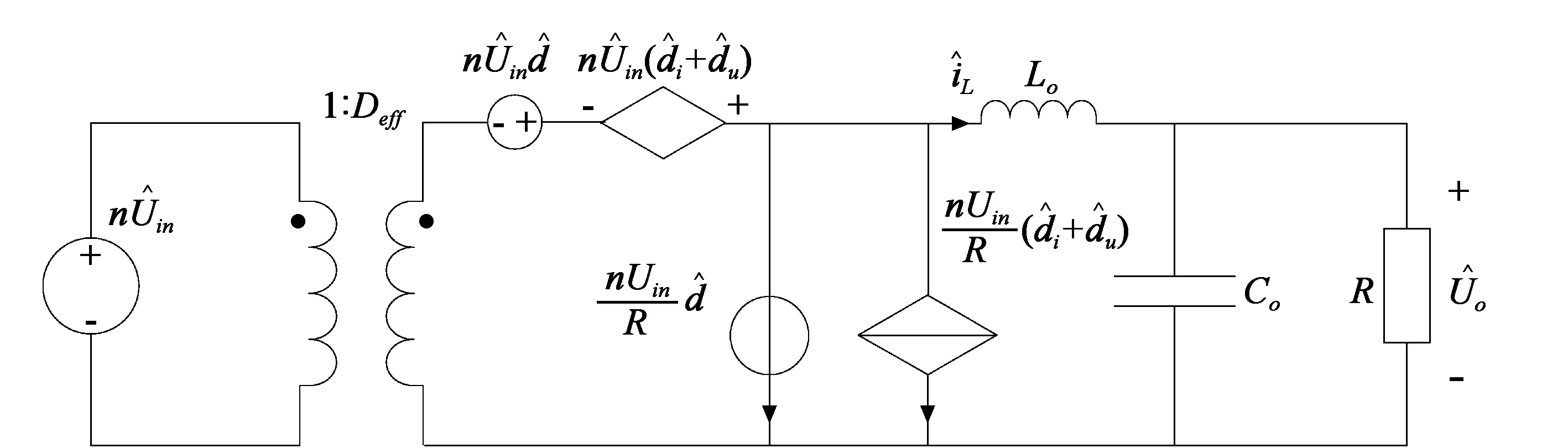
图5 移相全桥变换器小信号模型

(7)

同理，求得负载传递函数Zo(s)为

(8)

3.2 双闭环控制系统设计

以上分析了移相全桥电路系统结构组成，并建立了变换器系统数学模型，图6为实际变换器双闭环控制系统结构框图。

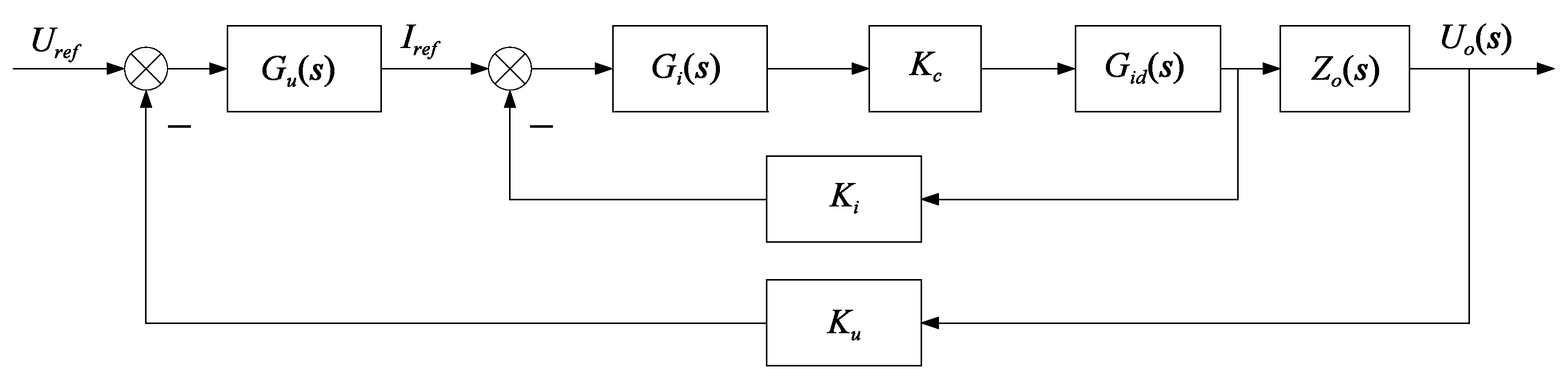
图6 实际变换器双闭环控制系统结构框图

在图6中，Gu(s)为电压环PI调节器，Gi(s)为电流环PI调节器，Kc表示PWM波的三角载波系数，Gid(s)为电感电流对占空比的传递函数，Zo(s)为输出负载传递函数，Ku为电压霍尔的反馈比例系数，Ki为电流霍尔的反馈比例系数。由于此系统为电压电流双闭环控制系统，按照工程设计方法首先从电流内环的参数开始设计，在获得稳定内环后，可得到电流内环的闭环传递函数，将其作为电压环中的一个环节，进而完成电压环调节器参数设计[8]。通过调整电流内环和电压外环的比例系数和积分时间常数，使系统的相位裕量大于45°，保证系统具有较强的稳定性[10]。为减少设计复杂性，可使用MATLAB中自带的SISOTOOL工具箱，并根据系统超调情况及希望得到的幅频特性和相频特性设计出合理的调节器参数。变换器主电路关键参数的设计应按照用户要求合理设计，不同应用场合变换器参数的设计方法[12]不尽相同。本变换器系统的主电路参数如表1所示。

表1 变换器主电路参数

将主电路参数带入式(7)，然后用MATLAB计算得到电流内环中传递函数Gid(s)，取Kc=1/2.5，最终计算得到传递函数Gid1(s)为

(9)

在MATLAB命令行中输入SISOTOOL，令G=Gid1，Ki=0.05，设电流内环和电压外环的PI调节器的一般形式为

(10)

(11)

式(10)和式(11)中Kpi和Kpu为电流调节器和电压调节器的比例系数，Ti和Tu为电流调节器和电压调节器的积分时间常数。根据其PI调节器的一般形式，在SISOTOOL的根轨迹图中加入一个零点和一个极点，且极点设置为0，然后拖动鼠标设计合理的电流内环调节器参数。完成电流环设计后，依据以上设计原则进一步设计电压外环调节器参数，取Ku=0.020 8，同理完成电压外环设计，最终设计的控制器参数如表2所示。

表2 控制器参数

将上述参数带入式(1)，参照图6所示的变换器闭环结构框图，在MATLAB中画得电流内环和电压外环的PI调节开环频率特性，如图7和图8所示。

从图7可知，经调节器补偿后的系统截止频率为9.6×104rad/s，相位裕量为88.3°，满足系统稳定性要求。图8所示为变换器系统开环频率特性，从图中可见，变换器系统相位裕量为55.3°，截止频率为6.47×104rad/s，小于电流内环的截止频率，系统能满足稳定性和动态响应要求。

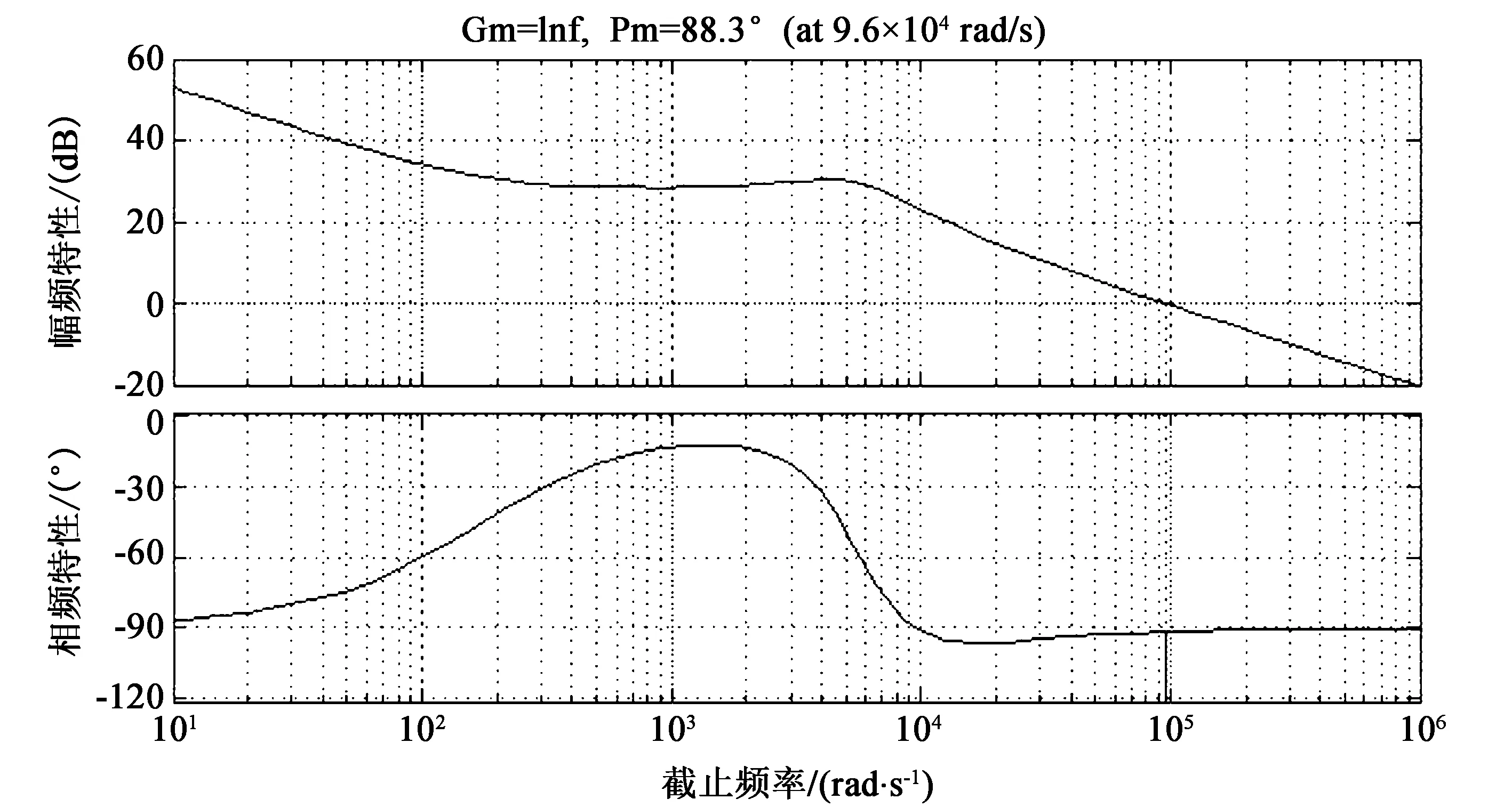
图7 调节器补偿后的电流内环开环bode图

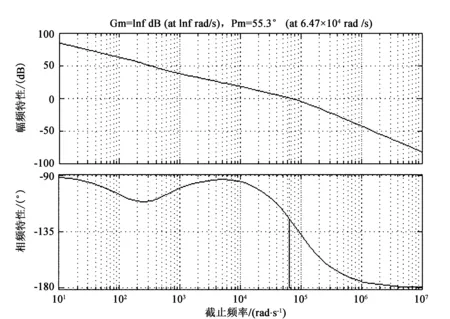
图8 双闭环系统的变换器开环bode图

4 实验结果

图9中②示出了超前臂开通和关断时MOSFET的驱动电压Ugs实验波形；③示出了满载时变压器的初级电流IP实验波形，其实验波形与图2中的理想波形基本一致；④示出了直流400 V输入时源漏极电压Uds实验波形，可见，超前臂实现了零电压开通和关断(ZVS)。接着对该变换器系统进行效率测试，结果如图10所示。由图10可知，当接入负载电流Io=40 A时，输出电压Uo=48.022 V，此时开关变换器达到最高工作效率，即η=95.2%。

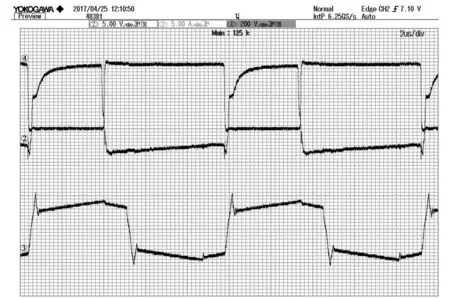
图9 额定输入满载时实验波形

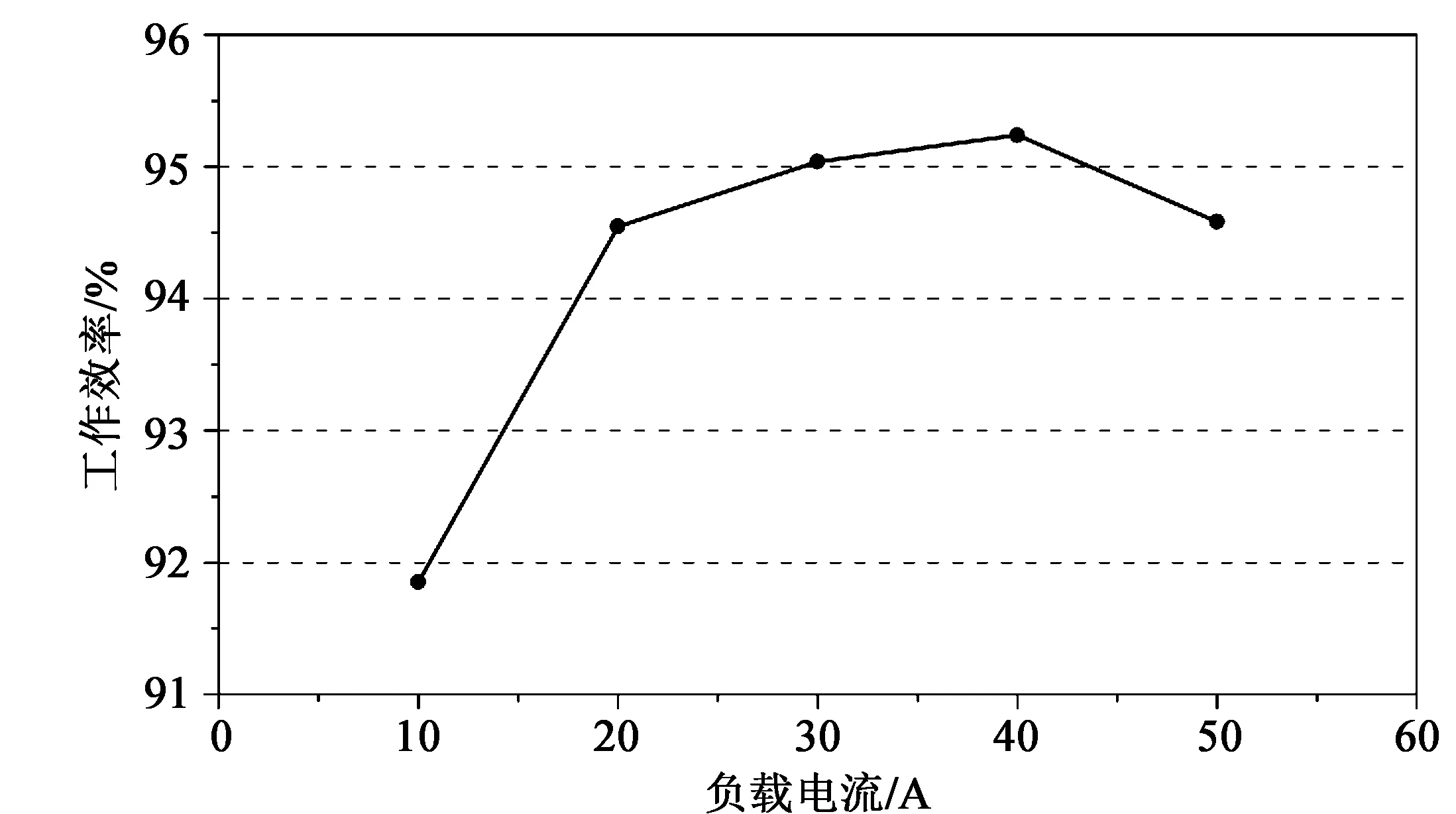
图10 变换器效率变化曲线

为探究该变换器输出电压精度，对变换器工作在额定电压工况下，不同负载电流情况下的输出电压进行了实际测量，表3给出了电压测量的实验结果。

表3 实验测量的输出电压结果

由表3实验测量的输出电压结果可知，输出电压Uo的稳压精度在0.12%以内，在规格书要求的稳压精度(≤0.5%)范围内，满足设计要求。

5 结束语

本文基于移相全桥软开关技术，设计了48 V/50 A开关电源模块，同时建立了控制电路数学模型，并进行了仿真分析，最后对实物样机完成了实验测试。仿真和实验测试结果表明，该电源设计方案可行，各项指标均满足设计要求。

[参考文献]

[1] GAO Yun,YANG Min.Design and Simulation of ZVZCS Phase-Shifted Full Bridge PWM Converter.IEEE Conference Publication[C].Xi’an:2016 International Symposium on Computer,2016:923-925.

[2] 陈坚,康勇.电力电子学-电力电子变换和控制技术[M].北京:高等教育出版社,2011:270-274.

[3] 梁永清,黄志强.双闭环控制的移相全桥软开关变换器的研究[J].现代电子技术,2014,37(8):156-158.

[4] 岳鹏,田联房.数字控制全桥软开关电源的Saber仿真分析[J].科学技术与工程,2010,10(10):2526-2530.

[5] 陈轶涵,韦徵,龚春英.平均电流控制型移相全桥DC-DC变换器输出阻抗及控制环路优化设计[J].电工技术学报,2013,28(4):43-49.

[6] VLATKOVIC V,SABATE J A,RIDLEY R B,et al.Small-signal analysis of the phase-shifted PWM converter[J].IEEE Transactions on Power Electronics,1992,7(1):128-135.

[7] HU Xue-zhi,NAN Guan-qun.The Research of Modeling and Simulation for Phase-shifted Full-bridge ZVS DC/DC Converter[C].Nanchang:International Conference on Intelligent Information Technology Application,2009:549-552.

[8] 陈国超,张昆仑.移相全桥ZVS ZCS变换器双闭环控制系统设计[J].通信电源技术,2010,27(5):20-23.

[9] 亓立博.三电平拓扑结构变换器过电压行为的抑制研究[J].陕西理工学院学报(自然科学版),2016,32(1):34-38.

[10] 陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,1997:59-88.

[11] 杜道昶,田丽,赵明敏,等.新型高增益Boost变换器设计[J].陕西理工学院学报(自然科学版),2015,31(1):22-25.

[12] 史永胜,刘言新,王喜锋,等.移相全桥ZVS变换器的优化及参数设计[J].电子器件,2016,39(3):650-654.