多场作用下含非绝缘裂纹的压电材料断裂研究❶

邢时超 (铜陵学院机械工程学院，安徽 铜陵 244061)

近年来，越来越多学者开始关注压电材料，在理论研究和实验验证的基础上使得压电理论得到健全和完善[1～3]。压电材料具有很多优良的性能，但它属于脆性材料，在工程实践中容易产生裂纹，特别当材料中存在夹杂或孔洞的情况以及外载情况复杂的时候。而一旦压电材料存在或产生裂纹之后，裂纹容易扩展，这将严重影响压电构件的性能和寿命。关于含裂纹压电材料的断裂研究，就变得很有工程实际意义。

压电构件存在裂纹是常见现象。高存法和樊蔚勋[4]研究了含裂纹压电材料的二维问题，应用Stroh公式和精确的电边界条件，得到了场强度因子和能量释放率的精确解；Guo和Noda[5]研究了含穿插界面裂纹的功能梯度层状结构的动态响应，附加平面内部的冲击载荷。热载荷对于压电材料的作用也是研究的热点之一。陈星烨和唐雪松[6]研究了均匀热流作用下含裂纹板Ⅰ型温度应力强度因子的解析解；S.Ueda[7]研究了功能梯度压电材料的热-机-电断裂问题；Wang和Gao[8]研究了含椭圆孔的压电体在孔边衍生边界裂纹时的电弹性解。目前，关于含热半穿透裂纹的压电材料断裂问题研究较少，而在实际情况下，随着构件的使用出现裂纹会越来越多，而裂纹的绝缘性不再是初始的假想状态(热绝缘或热全穿透)。下面，笔者结合复变函数法和Hilbert问题解法来研究热-电载荷作用下含非绝缘裂纹的压电材料断裂问题。

1 理论分析

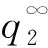
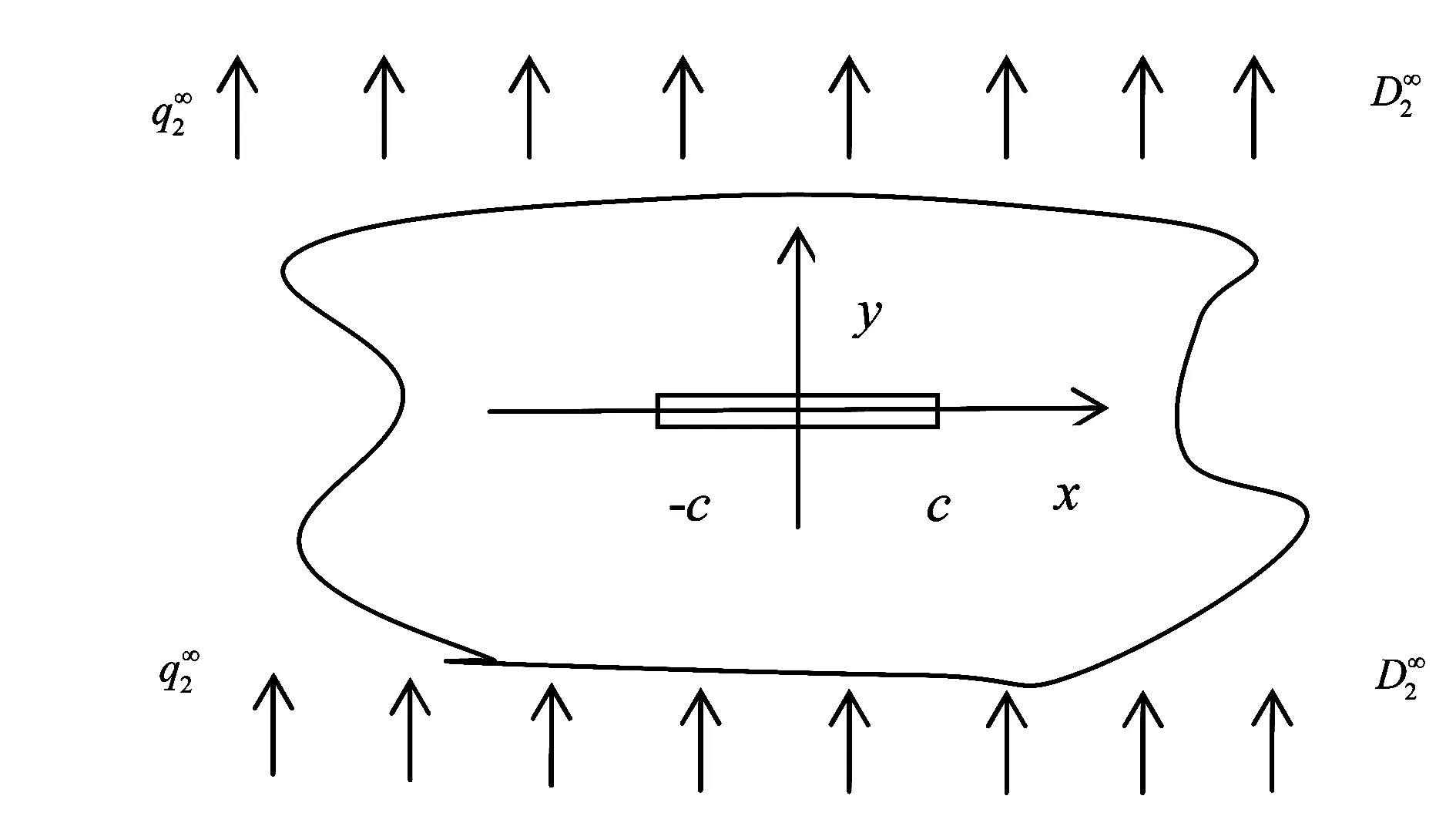
图1 压电板边界条件

1.1 基本公式

考虑压电材料在无穷远处受热-电载荷作用，其温度场和电弹性场的基本方程如下。

温度场控制方程:

qi,i=0

(1)

温度场本构方程：

qi=-αijT,j

(2)

式中，下标的逗号表示微分，并采用求和约定；qi为热流矢量；αij为热传导系数；T为温度；i、j表示直角坐标，且i、j=1、2。

由式(1)和(2)可以得到温度场表达式：

T=2Re[g′(zt)] (zt=x1+μtx2)

(3)

电弹性场本构方程：

σij=cijklεkl-ekijEk-λijT

(4)

Di=eiklεkl+∈ikEk+piT

(5)

将式(4)和(5)带入弹性场平衡方程：

cijkluk,lj+ekijφ,kj-λijT,j=0

(6)

eikluk,li-∈ikφ,ki+piT,j=0

(7)

式中，σ为应力张量；ε为应变向量；E为电场向量；D为电位移向量；u为位移向量；cijkl为材料常数；ekij为压电常数；∈ij为介电常数；pi为常数；φ为电势向量。

引入广义位移函数u=(u1,u2,u3,φ)T以及广义应力函数φ=(φ1,φ2,φ3,φ4)T，通过求解方程(6)和(7)的通解和特解，最终表示为：

u=2Re[Af(z)+cg(z)]

(8)

φ=2Re[Bf(z)+dg(z)]

(9)

式中，A、B为二维问题Stroh公式特征向量的矩阵形式；c、d为热特征向量。

1.2 温度场

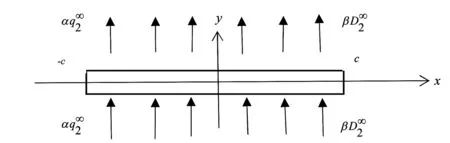
图2 裂纹表面边界条件

裂纹表面边界条件如图2所示，在裂纹界面上，热边界条件为:

(10)

式中，α为热绝缘系数；β为电绝缘系数。热复函数g′(zt)可以由下式表示：

(11)

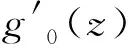
根据温度场本构方程(2)及其表达式(3)，令z→∞，可得：

(12)

(13)

根据公式(12)和(13)可得到m1：

(14)

将图2中的边界问题转化成第二类Riemann-Hilbert边值问题，得到公式：

(15)

(16)

从而得出温度场函数为：

(17)

1.3 电弹性场

由图2可知，电弹性场的边界条件为：

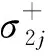
(18)

(19)

(20)

类似于热复势函数，依据位移及电势的单值条件，同样可以将电弹性场复势函数表示成多个部分组成，其形式为：

(21)

根据式(8)和(9)可以得到：

u，1=2Re[Af′(z)+cg′(z)]

(22)

φ，1=2Re[Bf′(z)+dg′(z)]

(23)

将电弹性场复势函数式(21)代入式(22)和(23)，然后令z→∞，可得：

(24)

(25)

(26)

(27)

得到:

(28)

进而求得：

(29)

式中，a0可由位移单值条件和力电平衡条件求得。

1.4 场强度因子

场强度因子的表达式：

(30)

式中，k为场强度因子；kΠ为同平面剪切型(滑移型)裂纹应力场强度因子；kⅠ为张开型裂纹应力场强度因子；kⅢ为反平面剪切型裂纹应力场强度因子；kD为电位移场强度因子。

将式(23)代入式(30)可得：

(31)

2 数值模拟

考虑材料为横观各向同性的压电板，假定x1-x2面为各向同性面，x3轴为极化方向。采用硒化镉为模型材料，由其材料常数可以求得矩阵A、B:

图3 裂纹延长线上的热流

注：红线对应括号内KⅠ数值。 图4 热流作用下应力强度因子随热绝缘系数变化 图5 KD，KⅠ随裂纹长度变化

3 结论

研究了热电载荷作用下含半绝缘裂纹的无限大压电平板的断裂问题。通过复变函数法和Hilbert问题解法，求出温度场、电弹性场以及场强度因子。通过数值模拟，得出以下结论：

1)在裂纹尖端处，热流存在奇异性，并在距尖端远处趋于入射热流；

2)强度因子场向量在裂纹长度固定时随绝缘系数α、β均成线性变化，在无电场作用的情况下，其随热绝缘系数呈线性变化；在无热流作用的情况下，其同样随电绝缘系数呈线性变化；

3)2种强度因子KD和KⅠ随裂纹长度呈椭圆线变化，绝缘系数α越大越趋于平稳；

4)应力强度因子随着热流的增加而单调增加。

[参考文献]

[1]Hetnarski R B, Ignaczak J. The mathematical theory of elasticity[M]. 2nd ed. New York：Taylor & Francis, 2011.

[2] 王保林. 压电材料及其结构的断裂力学[M].北京：国防工业出版社, 2003.

[3] 范天佑. 动态断裂力学原理与应用[M].北京：北京理工大学出版社，2006.

[4] 高存法, 樊蔚勋. 压电介质内裂纹问题的精确解[J]. 应用数学和力学, 1999, 20(1):47～54.

[5] Guo L C, Noda N. Dynamic investigation of a functionally graded layered structure with a crack crossing the surface[J]. International Journal of Solid and Structures, 2008, 45(1):336～357.

[6] 陈星烨，唐雪松. 均匀热流作用下含裂纹板I型温度应力强度因子的解析解[J]. 工程力学, 2012, 29(2):39～44.

[7] Ueda S. Transient response of a cracked piezoelectric strip under thermoelectric loading[J]. Department of Mechanical Engineering, 2006, 29(10):973～994.

[8] Wang Y J, Gao C F. Thermoelectroelastic solution for edge crack originating from an elliptical hole in a piezoelectric solid[J]. Journal of Thermal Stresses, 2012, 35(1):138～156.