库水位变动条件下岸坡渗流特性及稳定性研究
2018-05-02覃梦卿中国葛洲坝集团第一工程有限公司湖北宜昌443000
覃梦卿 (中国葛洲坝集团第一工程有限公司, 湖北 宜昌 443000)
储成龙 (江苏中南控股集团有限公司,江苏 海门 226124)
郭运华 (武汉理工大学道路桥梁与结构工程湖北省重点实验室,湖北 武汉 430070)
徐建雄 (湖北省汉江河道管理局,湖北 潜江 433100)
库水位变动是影响库岸边坡滑移破坏的一个主导因素[1,2],有统计显示,三分之二的水库在水位骤降时发生滑坡,三分之一的水库水位上升阶段发生滑坡[3]。塘岩光滑坡以及瓦依昂水库滑坡[4]发生后,库区水位变动诱发水库边坡稳定性问题才引起科研人员的空前重视。在已有的研究中大多数采用稳态渗流场作为计算依据,对于库水位变动引起的滑坡研究以均匀的水位升降速度为主[5~7]。随着对库岸滑坡更深入地研究,国内外学者发现瞬态渗流场对边坡稳定性影响更加显著,同时边坡材料非均质性的影响也得到广泛关注。当前,在库水位升降作用条件下的边坡破坏机制研究还有待进一步加强,主要体现在库岸边坡岩体物理力学参数变化,对库水位变动条件下的边坡稳定性影响尚缺乏系统深入的研究[8],也较少考虑瞬态饱和非饱和区对库岸边坡稳定性的影响[9,10]。下面,笔者以大岗山右岸坝肩枢纽区边坡作为研究对象,采用更符合库区形态的正弦余弦函数作为水头边界函数,分析库岸边坡在水位变化过程中,渗流场影响范围的边坡局部稳定性与边坡全局稳定性演化规律,并确定水库水位升降的速度控制标准。
1 库水位变动条件下的边坡稳定性分析原理
1.1 库水位变动条件下的水岩作用原理
水岩作用首先由前苏联A.M.O Bynhhnkob于20世纪50年代提出,库水位变动过程中水与岩土体的物理作用包括侵蚀作用和软化作用,主要包括库水位升降过程中水对岩体的静、动水渗透压力作用,超孔隙水压力效应以及岸坡淹没部分的浮力作用。当库水位上升和下降时,分别形成指向坡内坡外的动水渗透压力。动水渗透压力越大,越容易导致岸坡失稳破坏;较大的超孔隙水压力,使压密区抗剪强度急剧减小,岸坡失稳概率提高;浮力会提高滑坡体的失稳可能性。
1.2 饱和-非饱和渗流控制方程
二维渗流的一般控制微分方程如下:
(1)
式中,h为水头;kx为x方向饱和渗透系数(x为水平方向);ky为y方向饱和渗透系数(y为垂直方向);Q为边界上的流量;θ为单位体积含水量;t为渗流时间。
饱和-非饱和情况下的有限元控制方程为[11]:
(2)
式中,mw为储水曲线的斜率;γw为水的容重;H为总水头。
1.3 边界条件
在瞬态分析中,边界条件可以是时间的函数,也可以是存在于流动区域或者进入流动区域流量的函数。假定库水位上升与下降互为逆过程,可选用正弦或余弦函数来描述库水位升降条件下总水头与时间的函数关系[12~14]。当库水位上升时,边坡边界总水头与时间的正弦函数表达式为:
(3)
式中,h(t)为总水头,是时间t的函数;Δh为正常蓄水位与枯水位的差值;T为库水位上升的总时间;t为库水位上升时的各时间节点;h0为枯水位高度。
当库水位下降时,定义的岩坡体边界总水头与时间的余弦函数关系式为:
(4)
1.4 裂隙岩体非饱和渗流特性及等效化
对于裂隙饱和渗流规律可用立方定理描述,对于裂隙网络中的非饱和渗流,一般认为节理的几何特征、裂隙中水的饱和度、流体性质等均对裂隙的非饱和渗透性质有影响。胡云进等[15]通过实验认为岩石裂隙非饱和排水及吸湿过程具有非饱和土类似的特征,因此,将裂隙的非饱和渗流过程等效为连续多孔介质具有可行性,其中关键在于其REV(表征单元体体积)尺度的确定[16]。M.Wang et al[17]研究了4组节理迹长0.88~2m的随机节理岩体的三维渗流特征,其REV尺度为12m,这与张莉丽[18]的研究结果基本一致。陈亮[19]通过随机裂隙网络计算了大岗山边坡渗透系数张量,认为REV尺度为8m×4m。笔者研究对象满足连续介质的等效条件,因此采用Van Genuchten模型拟合非饱和渗透系数曲线[20,21]:
(4)
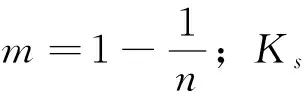
1.5 稳态与瞬态渗流分析
在进行瞬态渗流分析之前,首先确定各类岩体的非饱和渗透系数函数,然后定义渗流岩质边坡边界上所有结点的初始总水头。当库水位上升时,以初始地下水位线作为初始条件,作稳态渗流分析,在此基础上再作瞬态渗流分析;当库水位下降时,以正常蓄水位时稳态情况下的浸润线作为初始水位线,进而分析瞬态渗流情况。
1.6 边坡稳定性分析
由于大岗山水电站西部高山峡谷边坡地质条件复杂,由坡顶自然边坡残、坡积层逐步过渡到峡谷底部人工边坡的Ⅲ、Ⅳ类强卸荷岩体。同时顺坡面走向的卸荷裂隙发育带构成的潜在底滑面,使得边坡稳定性分析不仅要考虑水位变化影响强烈的局部稳定性,也需要分析边坡全局的稳定性演化,以全面评估水位变动对边坡稳定性的影响,稳定性分析采用极限平衡的Morgenstern-Price方法计算。
2 水位变动条件下大岗山水电站右岸边坡渗流特性
2.1 工程概况
大岗山水电站位于大渡河中游,是四川近期开发的大型水电工程之一,坝址处控制流域面积达6.27×104km2,占全流域的五分之四。右岸边坡约1200~1300m高程以上为块碎石土,基岩岩性为灰白色、微红色中粒黑云二长花岗岩(γ24-1),局部出露辉绿岩脉(β)、花岗细晶岩脉(γL)等。据勘探揭示,右岸发育78条辉绿岩脉,8条主要花岗细晶岩脉,主要有β4、β97(f93)、β146、β168(f154)、β170(f244)、β202(f191)、β203(f194)等岩脉破碎带,岩脉破碎带呈块裂-碎裂结构。大岗山右岸边坡地形及地质剖面如图1所示,节理、裂隙统计规律如表1所示。

图1 大岗山右岸边坡地形及地质剖面图
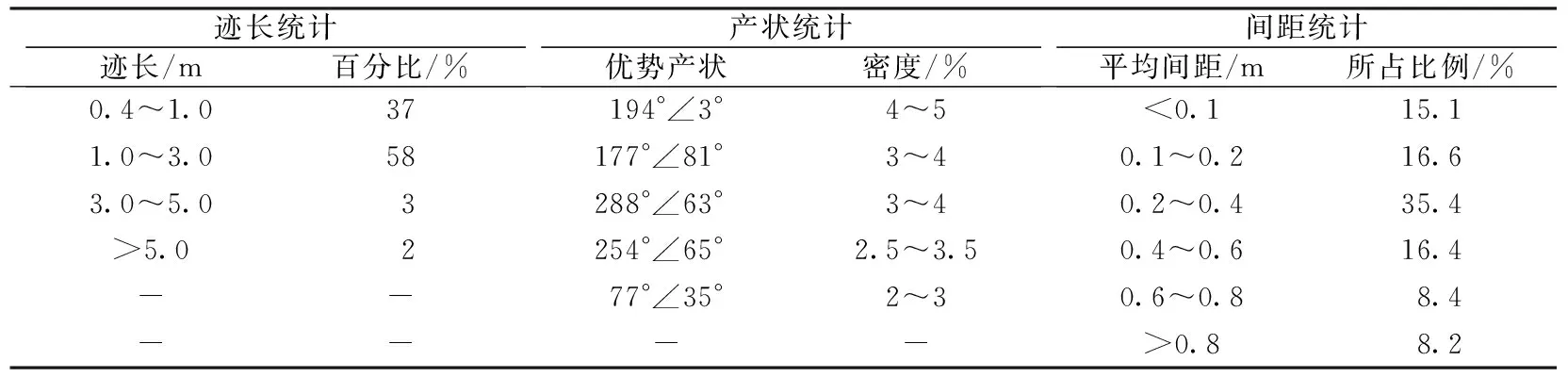
迹长统计迹长/m百分比/%产状统计优势产状密度/%间距统计平均间距/m所占比例/%0.4~1.037194°∠3°4~5<0.115.11.0~3.058177°∠81°3~40.1~0.216.63.0~5.03288°∠63°3~40.2~0.435.4>5.02254°∠65°2.5~3.50.4~0.616.4--77°∠35°2~30.6~0.88.4---->0.88.2
2.2 计算参数
根据勘察设计单位推荐的各分区岩体力学参数取值如表2~表4所示。

表3 主要结构面抗剪强度参数表

表3 坝址区各类岩体和结构面的渗透系数建议值
2.3 水位变动条件下渗流场演化规律
根据大岗山水电站的水文地质资料,从枯水位蓄水至正常蓄水位时间长短分为4个方案进行研究,分别为30d蓄满、90d蓄满、150d蓄满、270d蓄满;放空方案依据从正常蓄水位降至枯水位分为4个方案进行研究,分别为30d放空、90d放空、150d放空、270d放空,不同水位变动速率条件下坡内渗流场演化规律如图2所示。

图2 不同水位变动速率条件下坡内渗流场演化规律
由图2(a)~(d)可知,浸润线从初始地下水位线逐渐上移,浸润线在库岸边坡的较深部区域的变动幅度较弱,在边坡较浅层区域的变动幅度更加明显。30d快速蓄满方案中,随着库水位的不断上升,滑坡体内逐渐形成“倒流”现象,坡体浸润线上升滞后于库水位上升,形成库区水体向坡内的补给。当蓄水速度降低到90d蓄满时,浸润线的形成基本为库水位抬高坡内地下水位。对比4个方案可知,蓄水速度越快,地下水位变化滞后越明显,曲线下凹程度越严重;反之,水库蓄水时间越长,浸润线向下凹的程度越小,库水位变化的滞后效应越低,且地下水渗流场的影响范围更广。
由图2(f)~(i)可知,最下部分的浸润线是库水位从正常蓄水位下降至枯水位时的浸润线。浸润线在库岸边坡较深区域变动幅度更弱,较浅层区域变化幅度更加明显。从4个方案计算结果对比可以判断,浸润线在库水位下降时呈现上凸状,库水位下降时,坡体中的浸润线总是滞后于库水位边界水头的下降速度,坡内水体向库区补给;当库水位下降速度较快时,边坡内水位线下降滞后于库水位下降。降水速度越快滞后效应越明显,曲线上凸程度则越严重;由于断层渗透系数远大于周围岩体,快速放空时,出现了断层部位,浸润线产生突变。
3 水位变动条件的下边坡稳定性
3.1 局部稳定性分析
水位变动条件下的岩质边坡局部分析,也就是分析水位变化影响区在水位变动过程中的稳定性演化规律,分析方法是利用剪入剪出法在该特定区域搜索滑移面,分析库水位变动条件下库岸岩质边坡的渗流特性及其稳定性。局部边坡的滑移面的位置关系如图3、图4所示。
水位变化影响区的坡体渗流场浸润线与局部滑移面大部分情况都有交集,在库水位上升的后半段,由于坡体的形态滑移面浸没在水体中,浸润线随着库水位的上升而位于滑移面的上段。局部边坡的分析能够更直接将瞬态渗流场与边坡稳定性分析结合考虑,在分析库水位变动与边坡稳定性之间的关系具有针对性。以库区水位调控周期30d为例,得出库水位变动与边坡稳定性之间的关系,如图5和图6所示。由图5和图6可知,库水位上升时,局部安全系数先减小至最小值随后不断增大,高水位时略有减小;库水位下降时,安全系数起初有波动,随后不断减小至最小值后略有抬升。从安全系数的波动曲线可以确定水变化影响区的最危险水位,该水位在高程980.7m位置处。
3.2 全局稳定性分析
大岗山右岸边坡全局稳定性分析基于2点考虑:①坝顶以上边坡岩体风化卸荷强烈, V类强风化岩体内可能形成均质材料的潜在圆弧滑动破坏;②由断层f218、f231(见图1)形成另一种可能的深部滑动面。边坡全局稳定性控制区域如图7所示,库水位变动期边坡全局稳定性演化如图8所示。由图7和图8可知,蓄水前,f218、f231已完成预应力锚索与抗剪锚固洞结合的加固施工,计算结果表明,加固后的第2种破坏模式安全系数已达到1.4,第1种破坏模式安全系数更小。同时,在库水位变动条件下,无论第1种还是第2种破坏模式,库水位变动后坡体内的渗流场对边坡总体安全系数没有影响,原因是水位变动影响范围的边坡具有足够的稳定性,没有影响到上部坡体的稳定性。
4 结论
1)库水位上升时,浸润线呈下凹状,升速越大下凹程度越显著,渗流场影响范围越小;库水位下降时,浸润线呈上凸状,降速越大上凸程度越显著,渗流场影响范围越小。
2)无论是库区水位升高还是降低,水位变动影响区的局部库岸边坡稳定性都会产生变化。库水位上升时,安全系数先小幅减小随后不断增大,最后趋于一个稳定值;库水位下降时,安全系数先大幅减小到最小值,随后小幅抬升。如果水位变动影响区局部边坡稳定性足够,则边坡全局安全性可能不受水位变动的影响,因此水位变动条件下的库岸边坡稳定性需要综合评价,否则可能得出错误的结论。
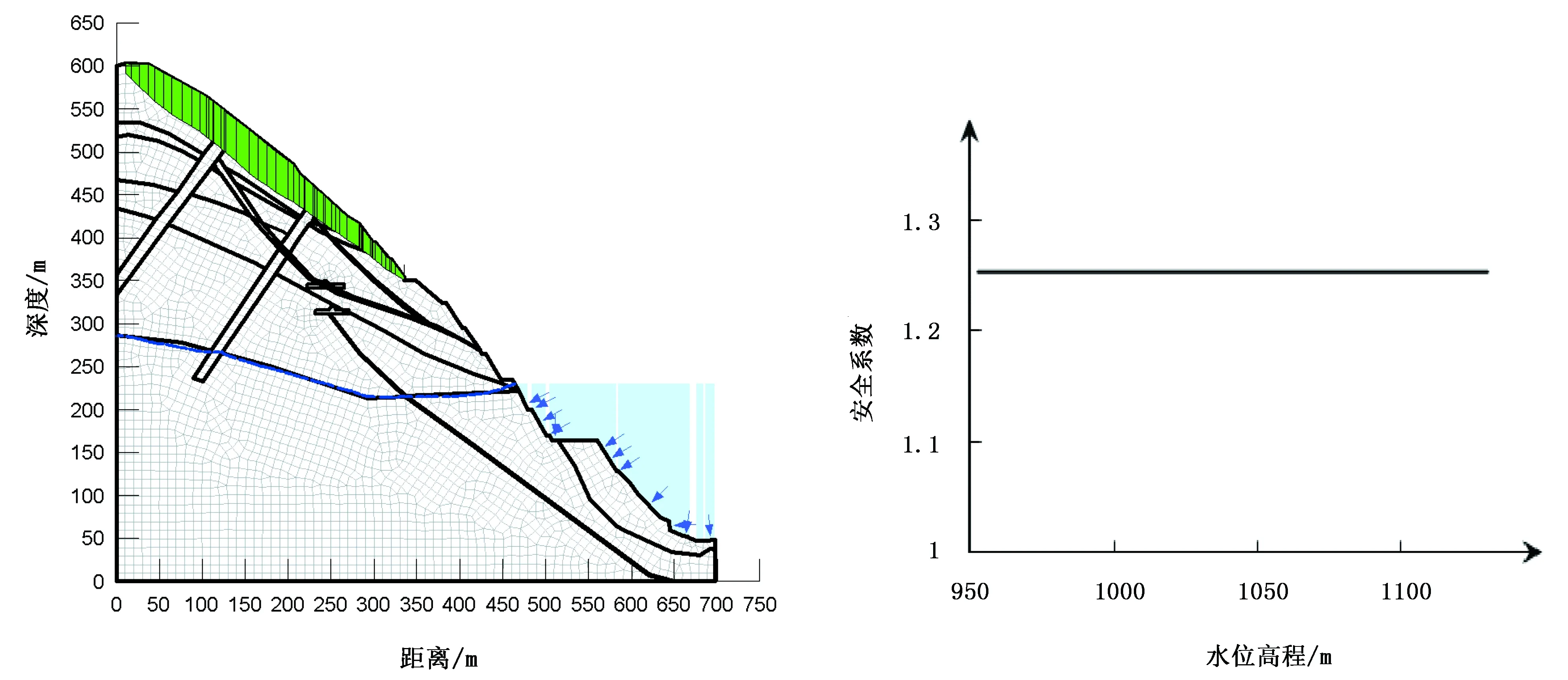
图7 边坡全局稳定性控制区域 图8 库水位变动期边坡全局稳定性演化
3)库区蓄水速度不是越慢就越安全,而是存在一个明显危险水位高程;水库放空过程中,边坡稳定性对降水速率更加敏感,需要严格控制水位下降速率。
[参考文献]
[1]朱冬林, 任光明, 聂德新,等. 库水位变化下对水库滑坡稳定性影响的预测[J]. 水文地质工程地质, 2002, 29(3):6~9.
[2]Louis C. Rock hydraulics in rock mechanics [M]. New York: Verlay Wien,1974.
[3]廖红建,高石夯. 渗透系数与库水位变化对边坡稳定性的影响[J]. 西安交通大学报,2006,40(1):88~92.
[4]Morgenstern N R. Stability Charts for Earth Slopes During Rapid Drawdown[J]. Geotechnique, 1963(13):121~131.
[5]柳群义,朱自强,何现启,等. 水位涨落对库岸滑坡孔隙水压力影响的非饱和渗流分析[J]. 岩土力学,2008,29 (增):85~89.
[6]郑颖人,时卫民,孔位学. 库水位下降时渗透力及地下水浸润线的计算[J]. 岩石力学与工程学报,2004,23(18):3203~3210.
[7]刘新喜, 夏元友, 练操, 等. 库水位骤降时的滑坡稳定性评价方法研究[J]. 岩土力学, 2005, 26(9): 1427~1432.
[8]钟声辉. 水岩体系中地下水效应与边坡稳定性研究[J]. 铁道工程学报, 1999, 16(4):86~90.
[9]莫伟伟,徐平,丁秀丽,等. 库水位涨落对滑坡稳定性影响研究进展[J]. 地下空间与工程学报,2006,2(6):997~1002.
[10]中村浩之.论水库滑坡[J]. 水土保持通报,1990, 10(1):53~64.
[11]储呈龙. 蓄水期坝肩枢纽区边坡渗流特性及稳定性研究[D]. 武汉:武汉理工大学, 2014.
[12]Nakamra H. Discussions on reservoir landslide[J].Bulletin of Soil and Water Conservation,1990, 10(1):53~64.
[13]雷红军, 冯业林, 刘兴宁. 糯扎渡水电站蓄水速度对心墙堆石坝安全的影响研究[J]. 大坝与安全, 2012(5):1~5.
[14]苏爱军. 湖北省三峡库区滑坡防治地质勘查与治理工程技术规定[M]. 北京:地质出版社,2003.
[15]胡云进, 钱锐, 速宝玉. 一种确定裂隙非饱和水力参数的数值模拟法[J]. 岩土工程学报, 2001, 23(3):284~287.
[16]Long J C S, Witherspoon P A. The relationship of the degree of interconnection to permeability in fracture networks[J]. Journal of Geophysical Research Solid Earth, 1985, 90(B4):3087~3098.
[17]Wang M, Kulatilake P H S W, Um J, et al. Estimation of REV size and three-dimensional hydraulic conductivity tensor for a fractured rock mass through a single well packer test and discrete fracture fluid flow modeling[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(7):887~904.
[18]张莉丽. 裂隙岩体渗透典型单元体存在性[D]. 北京:中国地质大学(北京), 2011.
[19]陈亮. 雾化条件下裂隙岩体水力学特征及对边坡变形的影响[D]. 成都:成都理工大学, 2013.
[20]Genuchten M T V. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils 1[J]. Soil Science Society of America Journal, 1980, 44(44):892~898.
[21]Fredlund D G, Xing A. Equations for the soil-water characteristic curve [J]. Canadian Geotechnical Journal, 1994, 31(4):521~532.
