基于鲁棒可靠性方法的机器人鲁棒镇定控制研究

张义辰

(上海理工大学 机械工程学院，上海 200093)

0 引 言

参数不确定性摄动是机器人有界摄动中的一种，它主要以有界函数的形式存在于机器人动力学模型的惯量矩阵、科氏力与离心力矩阵和重力矩阵中，是影响机器人轨迹跟踪稳定性的内在因素。这种不确定摄动通常是强耦合、非线性的，一般的方法很难将其分离，因此给后续稳定系统、改善其他性能带来了困难。为了减少这一类不确定因素的影响，学术上通常采用鲁棒控制的策略，考虑对参数摄动的最坏情况进行控制。然而对于具有不同特征的参数不确定摄动，仅仅依靠鲁棒控制不能发挥出很好的控制效果。

针对参数不确定系统的控制问题，国内外研究人员进行了大量的研究。郭书祥[1-2]提出了利用鲁棒可靠性的方法设计鲁棒镇定控制器优化系统；王恩平等人[3]讨论了带有分母多项式摄动的参数不确定性系统的鲁棒控制问题，设计了具体的控制器；谢蓉等[4]研究了范数有界型参数不确定性系统的鲁棒控制问题，并提出运用一种基于概率估计的鲁棒H∞控制方法，该方法经仿真实验验证合理有效；XU S J等[5]研究了带有非线性不确定参数的线性系统的简化和鲁棒性问题，通过等效变换和运算律，将非线性不确定参数与固定参数分离开来，变成等效的线性不确定参数，再研究其鲁棒特性；RIGATOS G等[6]提出了多自由度机器人的非线性H∞方法；黄文超等[7]将SOS理论和S过程相结合设计H∞控制器；RIGATOS G[8]应用H∞控制方法解决了多自由度机器人的最小最大微分博弈问题，使得机器人在干扰影响作用最大的时候状态变量误差达到最小；HWANG C L等[9]提出了一种混合H2/H∞离心离散变结构控制，用以解决不确定系统的鲁棒控制问题；JABALI M B A等[10]提出了一种将机器人模型转化为不确定凸多面体LPV模型的方法来稳定和优化机器人系统跟踪性能的方法。

本文将鲁棒可靠性的方法应用于机器人系统当中，设计鲁棒镇定控制器。

1 非线性不确定参数对机器人系统的影响

以平面两杆的机器人为模型，根据拉格朗日动力学原理建立机器人的动力学模型，该模型形如下式所示：

(1)

在机器人进行轨迹跟踪的场合，输入转矩通常是利用将轨迹代入式(1)中计算而得，计算的力矩表达式为：

(2)

式中：qd—期望轨迹；uc—控制输入；τd—理论输出转矩。

将式(2)代入式(1)，得到控制输入与轨迹误差之间的关系式如下：

(3)

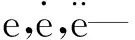
将式(3)改写为状态空间形式，为此设状态变量：

(4)

另有：

(5)

其中：

(6)

式中：I，0—2维的单位矩阵和全零矩阵；z—被调输出。

A、B当中最后一个矩阵块包含非线性函数，这些非线性函数高度耦合，并且以不确定参数q和q(·)为自变量，这些不确定参数会通过摄动影响机器人系统的稳定性和跟踪特性，需要运用有效的方法加以控制。然而在进行控制之前,必须先将它们从与固定的数值分离开来,一般的线性理论很难进行这一过程，即便分离出来,其形式也是相当复杂,不便于计算和整理。不过有一点可以确定，它们都是有界函数，需要运用一些技巧将它们作等效处理，再进一步确定界限值。

为了研究非线性不确定参数如何影响机器人的稳定性和跟踪性能，特给定一条确定的关节角轨迹：

(7)

式中：t—时间，s。

本研究通过Matlab/Simulink的仿真可得到两个关节角轨迹的跟踪效果，非线性不确定参数对轨迹跟踪效果的影响如图1所示。

可以看出：实际轨迹完全脱离期望轨迹，跟踪失败，并且就实际轨迹本身来看，其走势发散，呈现出比较大的振荡，说明系统不稳定。因此在保证系统稳定的条件下，设法控制非线性不确定参数的影响，兼顾稳定性与跟踪特性，是改善系统性能的有效方法，而欲实现这一点，就必须先对系数矩阵和输入矩阵中的不确定参数摄动项进行等效的处理，为确定该项的摄动上界提供便利。

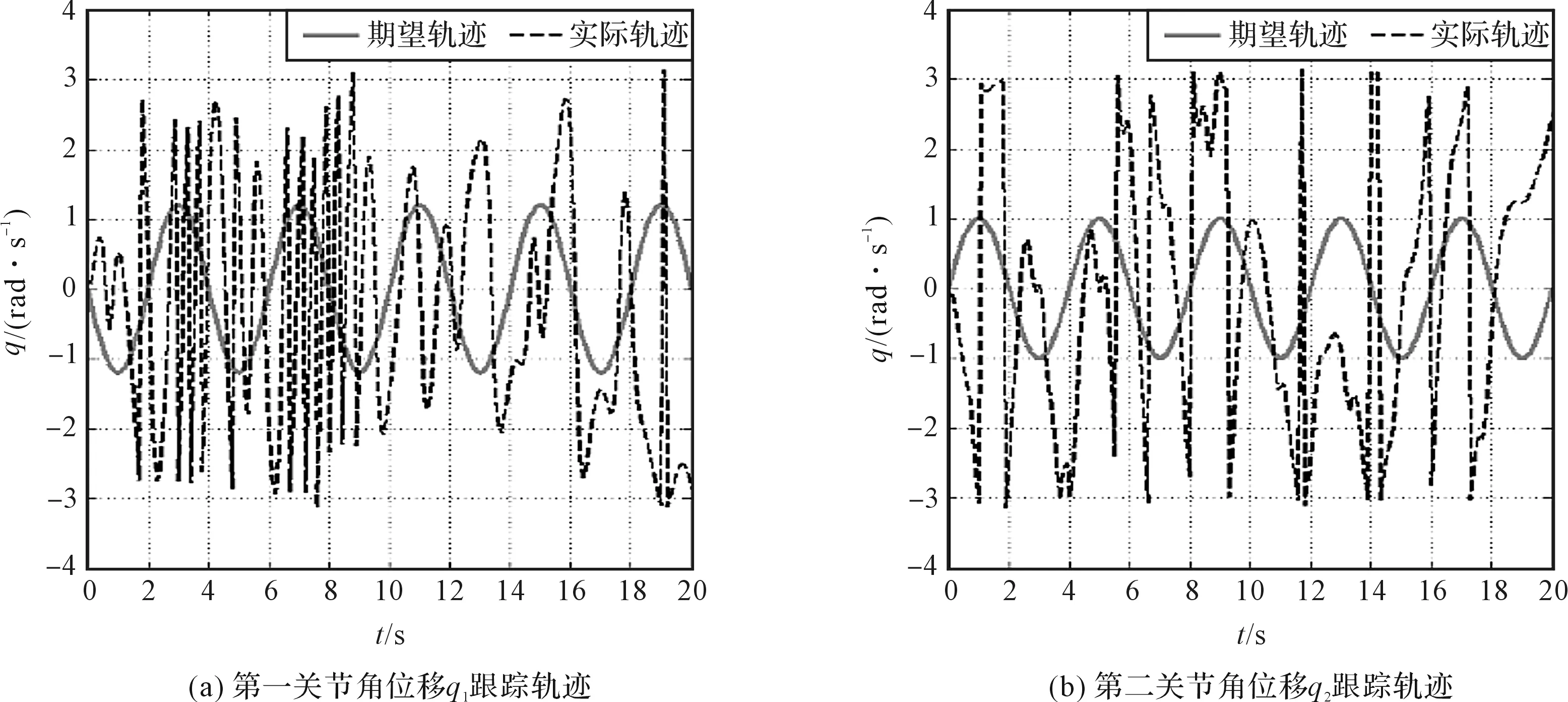
图1 非线性不确定参数对轨迹跟踪效果的影响实线—期望轨迹；虚线—实际轨迹

2 非线性参数的等效处理

对于式(3)所呈现的形式：

(8)

(9)

式中：M0,C0—惯性矩阵、科氏力离心力矩阵的标称量；ΔM,ΔC—惯性矩阵、科氏力离心力矩阵的摄动量。

则式(8)可以写为：

(10)

将式(10)写成状态方程的形式，即：

(11)

其中：

(12)

(13)

(14)

式中：0，I2——2×2的全零矩阵和单位矩阵。

根据公式：

(A+BCD)-1=A-1-A-1B(DA-1B+C-1)DA-1

(15)

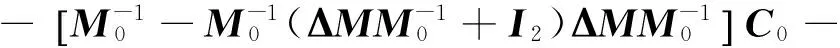
(16)

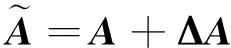
(17)

(18)

那么：

(19)

(20)

另一方面，由于：

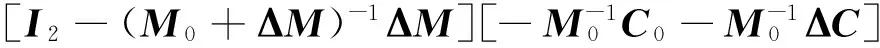
(21)

因此：

(22)

其中：

(23)

3 鲁棒可靠性与鲁棒控制器设计

3.1 鲁棒可靠性相关理论

对于如下所示的不确定时变系统

(24)

式中：x(t)—状态向量变量；uc(t)—输入向量变量；P(r)—状态矩阵；Q(r)—输入矩阵。

它们均随着不确定参数r的变化而变化。定义以状态反馈控制器：

uc(t)=-Wx(t)

(25)

系数矩阵W为需要设计的控制律，将控制器式(25)代入到系统式(24)中，原系统变为：

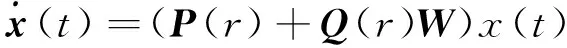
(26)

定义如果存在适当维数的对称正定矩阵P和矩阵K，使得对所有容许的不确定性有如下不等式成立：

(A(ρ)+B(ρ)K)TP+P(A(ρ)+B(ρ)K)<0

(27)

则系统可通过状态反馈二次镇定。

对于系统式(24)和控制器式(25)，显然应该保证：

(P(r)+Q(r)W)TY+Y(P(r)+Q(r)W)<0

(28)

成立。而对于有界的不确定参数r，可以通过固定量和摄动量的分离化为标准形式：

r=r0+dr·σ

(29)

式中：r0—r的名义值；dr—r的摄动值；σ—标准化的区间变量，σ∈[-1,1]。

据此，系统式(24)的系数矩阵P(r)和Q(r)可表示为随σ的变化而变化的值。

本研究定义以对称矩阵D(σ,Y),Y为式(11)中的可行矩阵，具体值未知，那么系统式(24)的稳定性问题可以归结为求矩阵不等式的可行解Y*：

D(σ,Y)<0

(30)

矩阵D(σ,Y)为鲁棒可靠性的功能函数，相应地有功能函数的鲁棒可靠度，其具体形式为：

(31)

式中：‖σ‖∞—σ的无穷范数，而区域Θ={σ:D(σ,Y)<0}和Θ={σ:D(σ,Y)≥0}分别对应标准化区间构造的无限拓扑空间中的可靠域和失效域。

从可靠性这一层面来看，β>0时系统的波动域和失效域无交集，判断系统为可靠的，如果随着β值的增加系统波动域与失效域相隔越远，系统在失效之前所能容许的不确定摄动越大，从而使系统在这些不确定量影响下的鲁棒性得到提高，系统可靠性更好。因此，鲁棒可靠度可以用来衡量系统鲁棒可靠性的好坏，并可以此为依据进行进一步系统的稳定化控制。

进一步地，对于系统式(24)，按分离不确定参数的步骤，系统中的矩阵P(r)和矩阵Q(r)可以写成：

P(r)=P0+ΔP=P0+S1Δ1S2,Q(r)=

Q0+ΔQ=Q0+T1Δ2T2

(32)

式中：S1,S2,T1,T2—权重矩阵；Δ1,Δ2—不确定摄动函数。

对于满足式(32)的系统式(24)，令k=||σ||∞,则矩阵不等式(30)对所有允许的不确定性成立，当且仅当存在适当维数的对称正定矩阵E,矩阵F和W，以及正定对角矩阵G1和G2，使得如下矩阵不等式成立：

(33)

其中：

(34)

相应地，基于鲁棒可靠性并考虑控制代价的控制器增益矩阵可由以下矩阵不等式求得，即有以下鲁棒可靠性优化问题：

(35)

式中：矩阵N与矩阵E同阶，且对称正定。

同时，由上述优化问题中参数k，可以进一步算出系统式(24)的鲁棒可靠度β=r-1，再由式(29)计算，即可求出使系统保持稳定的不确定参数r的最大鲁棒界限：

r∈[r0-(β+1)·dr,r0+(β+1)·dr]

(36)

3.2 鲁棒控制器设计

考虑了鲁棒可靠度的鲁棒控制器，可以根据不等式组(35)来求出，但在此之前，必须先计算出式(32)中两参数有界摄动量ΔP和ΔQ的上界，具体到本文研究的机器人系统式(22)，必须首先计算出附加项(ΔmA+Δa+ΔmΔa)和ΔmB的上界，因此：

|ΔmA+Δa+ΔmΔa|=|Δm||A|+|Δa|+|Δm||Δa|=
‖Δm‖∞×‖A‖∞+‖Δa‖∞+‖Δm‖∞×‖Δa‖∞=γ1

(37)

|Δm|=‖Δm‖∞=γ2

(38)

式中：γ1，γ2——正实数。

同时由式(37，38)所给出的上界的形式可以推断出左、右两边的系数矩阵，它们分别是：

S1=S2=I4,T2=B

(39)

对于式(33)中的参数k，可以通过计算：

k=‖(γ1,γ2)‖∞

(40)

至此，再利用Matlab的LMI函数包和可行性算法函数feasp()求出可行解E*和F*，最后利用下式：

W=F*E*-1

(41)

进一步地，使系统保持稳定的鲁棒可靠度和最大鲁棒界限：

βr=k-1

(42)

q∈[q0-(βr+1)·Δq,q0+(βr+1)·Δq]

(43)

4 实验及结果分析

本研究以提供的已知参数机器人为模型，数值验证将从优化前后、输入相同轨迹后的跟踪输出信号的时间序列出发进行比较，重点关注二者的瞬时值、误差值和H∞范数。

4.1 仿真验证

特以一两杆的机械臂为实例进行仿真验证，机械臂的已知参数如表1所示。

表1 两杆机械臂已知参数表

将已知数据代入上述机器人系统中，首先由式(37，38)算得：

γ1=2.578 8,γ2=5.158

(44)

计算：

k=‖(γ1,γ2)‖∞

(45)

得：

k=5.158

(46)

将k代入式(33)，计算式(35)的可行解[11]，最后由式(25)解得控制器的增益矩阵：

(47)

另求出使系统稳定的鲁棒可靠度：

βr=4.158

(48)

为了更直观地显示优化前后控制器的效果，笔者使用simmechanics模块建立两杆机械臂的物理模型，机器人的simmechanics结构如图2所示。

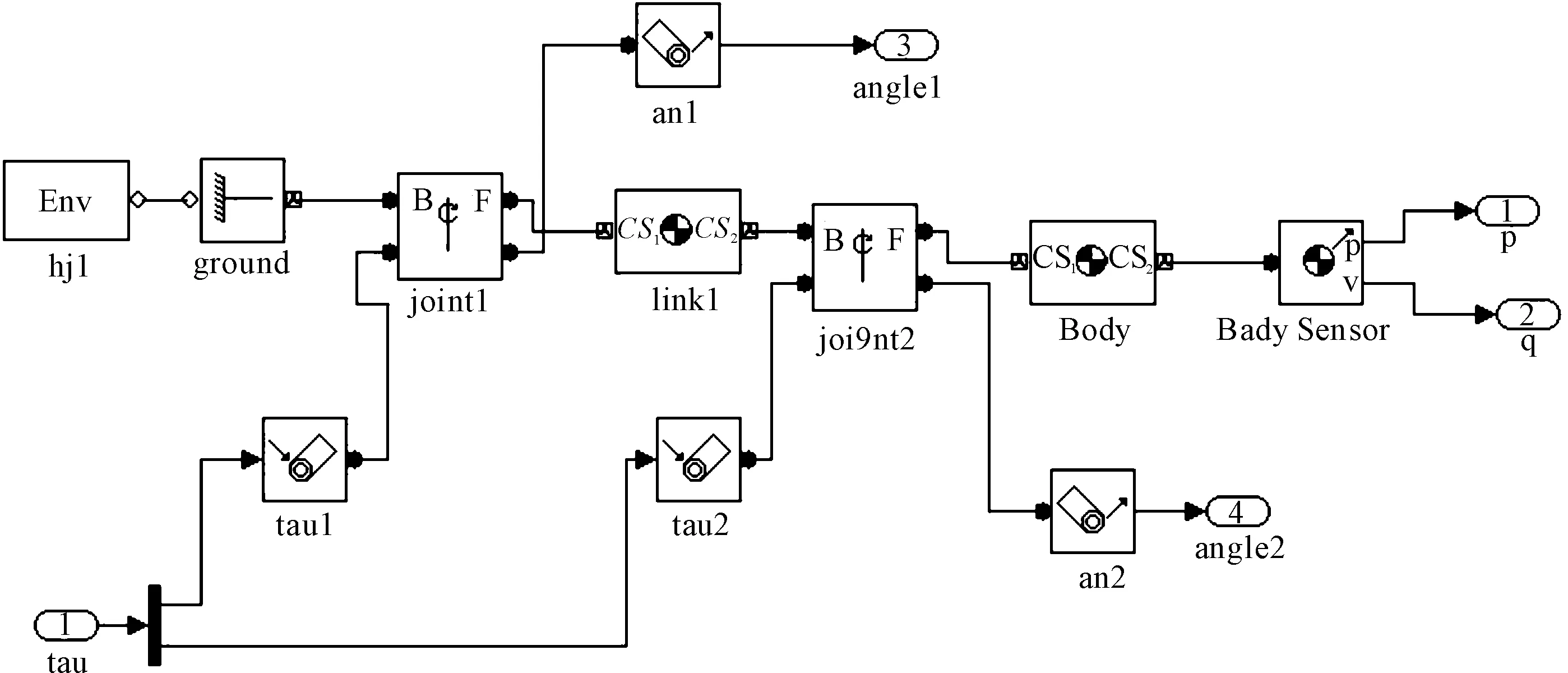
图2 机器人的simmechanics结构

机器人物理结构如图3所示。

图3 机器人的物理结构

本研究再将控制器接入机器人的跟踪系统模型中，通入形如式(7)的信号，并规定q(·)1=q(·)2=1 rad/s,观察优化前后的两个关节角轨迹的跟踪情况。为了更方便地观察优化前后控制效果的变化，笔者特将优化前的实际轨迹与误差、优化后的实际轨迹与误差合并画在同一坐标系当中，优化前后的控制效果对比如图4所示。

从跟踪效果的角度来验证，观察图4可以看出：优化前，虚线表示的实际轨迹和点划线表示的期望轨迹基本背离，对应的误差曲线(点划线)振幅较大，跟踪失败；优化后，图4(a，b)中的实践表示的实际轨迹与期望轨迹相当接近，但在靠近波峰和波峰下沿的部位有少许误差，这一规律通过图4(c，d)中的实践表示的误差曲线可以更直观的呈现，表明优化后的实际轨迹跟踪效果较优化前有明显的改善。

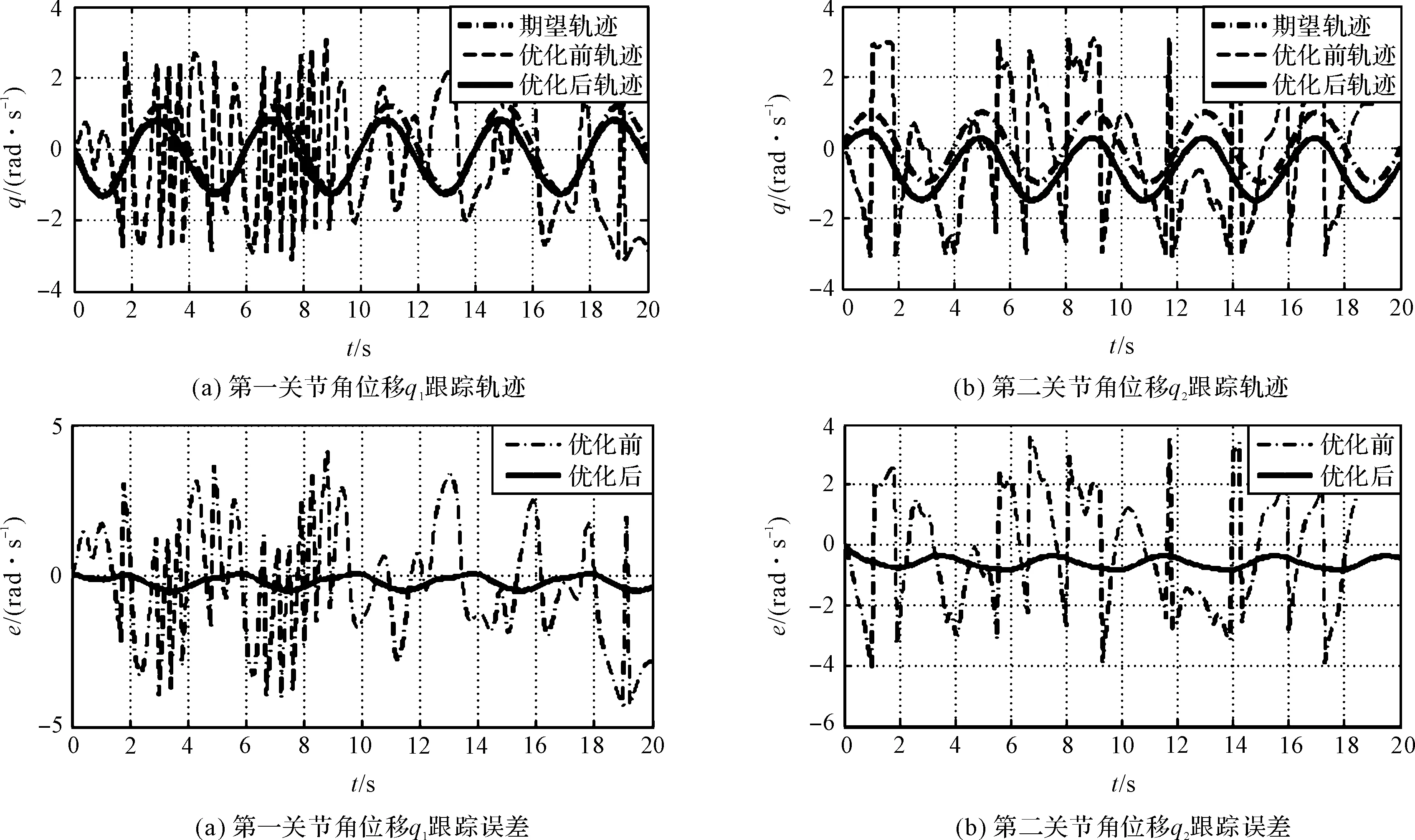
图4 优化前后的控制效果对比

从对控制力矩的改善效果来验证，优化前后的控制力矩对比如图5所示。

图5 优化前后的控制力矩对比

从图5可以看出：优化后的关节转矩较优化前提高了一部分，其中第一关节提高的幅度最大，说明随着系统性能的优化，机器人的控制力矩相应增加。

两方面的仿真验证结果都表明：经过新方法优化之后，机器人系统的稳定性得到了提高，跟踪性能得到了改善，控制力矩的控制作用也得到了相应的增加，新方法仿真层面可行。

4.2 数值验证

从数值角度验证系统在优化前后的变化效果，主要从两个方面入手，一方面比较优化前后两关节角实际轨迹和对应期望轨迹的时间序列，以及实际轨迹与期望轨迹的误差；另一方面比较优化前后系统的H∞范数。

首先，比较时间序列，为此笔者提取仿真试验采集到的输出角序列、参考输入角序列中从0～10 s的角度值，如表2所示。

表2 优化前后的角度时间序列对比

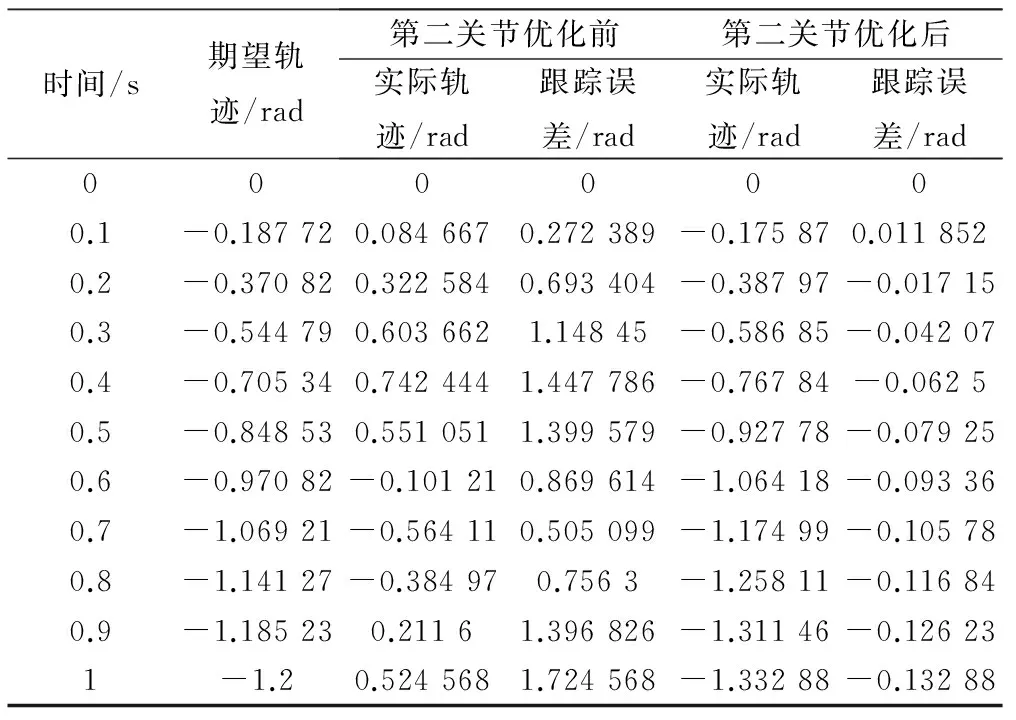
续表

对比第一关节中的期望轨迹、优化前的实际轨迹和优化后的实际轨迹，可以发现优化后轨迹的瞬时值比优化前更接近期望轨迹，并且优化后的误差值比优化前更接近0；同理，对比第二关节中的期望轨迹、优化前的实际轨迹和优化后实际轨迹，可以发现优化后轨迹的瞬时值比优化前跟接近期望轨迹，并且优化后的误差值比优化前也更接近0。这说明了新方法优化了跟踪轨迹的瞬时值，减小了误差，在稳定系统的同时改善了跟踪特性。

其次，比较优化前后系统的H∞范数。H∞范数是系统在环境最坏条件下的最大奇异值，它反映了系统的抗干扰能力。经计算，优化前系统的H∞范数：

V1≈1.91

优化前系统的H∞范数：

V2≈0.19

显然，V1>1,V2<1,V2

两方面的数值验证也表明：鲁棒可靠性方法对于改善系统的稳定性、跟踪特性、鲁棒性是十分有效的。

5 结束语

针对不确定参数摄动对机器人系统稳定性和跟踪特性的影响问题，本文采用鲁棒可靠性方法解决机器人的鲁棒镇定控制问题，效果可靠，将不确定因素的影响限制在了合理的范围内，稳定了系统，最大限度地保证了系统对给定轨迹的精确跟踪，改善了系统性能。

本文提出了运用鲁棒可靠性的方法来解决机器人系统的鲁棒镇定问题，把不确定参数的划定在一个具有足够可靠度的区间内；同时，本文也详细阐述了处理非线性摄动参数的简便方法,即分离固定值与摄动值后进行多项式的拆分与重组。

对于鲁棒可靠性方法，本文从仿真实验和数值比较的角度进行了验证，结果表明,该方法是有效的。

参考文献(References):

[1] 郭书祥.基于鲁棒可靠性方法的不确定系统最优二次鲁棒镇定控制器设计[J]航空学报,2007,28(6):1438-1442.

[2] 郭书祥.参数不确定系统鲁棒镇定控制器设计的鲁棒可靠性方法[J]系统工程与电子技术,2007，29(10)：1699-1703.

[3] 王恩平，黄 琳.一类参数不确定系统的鲁棒控制[J].自动化学报，2001,27(1):70-74

[4] 谢 蓉，王新民.范数有界型参数不确定系统的概率鲁棒H∞控制方法[J]控制与决策，2014，29(7):1-5

[5] XUA S J，DAROUACH M. On the robustness of linear system with nonlinear uncertain parameters[J].TechnicalCommuniques.1998,34(8):1005-1008.

[6] RIGATOS G,SIAO P. A nonlinear H-infinity control method for multi-DOF robotic manipulators[J].NonlinearDynamics,2016(1):1-20.

[7] 黄文超，孙洪飞.一类多项式非线性系统鲁棒H∞控制[J]控制理论与应用,2012,29(12):1587-1593.

[8] RIGATOS G, SIANO P. An H-infinity nonlinear control approach for multi-DOF Robotic manipulators[J].IFAC-Pape-rsOnline.2016,49(12):1406-1411.

[9] HWANG C L, HAN S Y. H∞design for a decentralized discrete variable structure control with application to mobile robots[J].IEEETransactionsonSystems,Man,andCybernetics-partB:CY-Bernetics,2005,35(4):736-750.

[10] JABALI M B A, KAZEMI M H. Uncertain polytopic LPV modelling of robot manipulators and trajectory tracking[J].InternationalJournalofControl,AutomationandSystems,2017,15(2):883-891;

[11] 俞 立.鲁棒控制—线性矩阵不等式处理方法[M].北京：清华大学出版社,2002.