基于最优控制迭代学习算法的收敛性研究*
2018-05-02杨亮亮
杨亮亮,胡 建
(浙江理工大学 机械与自动控制学院,浙江 杭州 310018)
0 引 言
迭代学习控制适用于执行重复任务的控制系统,不需要被控对象的精确数学模型,利用信息改善当前的控制输入信号,就可以实现有限区间内的完全跟踪[1-2]。文献[3-4]对迭代初态与期望初态存在固定偏移情形下的迭代学习控制问题进行了讨论,提出带有反馈辅助项的PD型迭代学习控制算法,可实现系统输出对期望轨迹的渐近跟踪。
李岩等[5]将传统的迭代学习控制时域和频域分析方法扩展到一类分数阶非线性系统,提出了一类新的分数阶迭代学习控制框架并简化了收敛条件,且证明了常增益情况下两类分数阶迭代学习控制收敛条件的等价性问题;文献[6-7]提出了基于当前误差和前次运行误差信息的P-D型开闭环迭代学习控制律,采用了λ范数和一系列不等式技术,通过建立精确数学模型给出了该学习律收敛的充分条件,证明了它的收敛性;LUO Z等[8]采用P型迭代学习控制率,对算法收敛性和收敛速度进行了分析,并通过实验对其进行了验证;童少伟[9]以线性系统为模型,以系统响应与期望响应的差值为反馈,以二次型性能泛函为目标函数,通过迭代学习修正主动控制器控制信号,并给出了该方法收敛的充分条件,但是缺少对算法收敛速度的分析与研究。
本文将在上述文献的基础上,基于最优控制理论以误差最小和驱动能量最小为性能目标函数,通过引入一个加权系数矩阵,以提高迭代学习算法的收敛速度。
1 迭代学习控制
本文将迭代学习控制算法运用到直线伺服系统进行分析,假设直线电机在每次迭代时执行时间长度t∈[0,T],采样周期为Ts,输入理想轨迹指令为rset,将信号进行离散化处理,取N=T/Ts,如第k次输出信号为yk=[yk(0),yk(1),…,yk(N-1)]T。其中,yk(j)—第k次迭代时,输出信号yk的第j+1个元素;yk—时域离散化向量。不考虑非线性因素的影响,则直线电机运动控制系统的时不变离散状态空间表达式为:
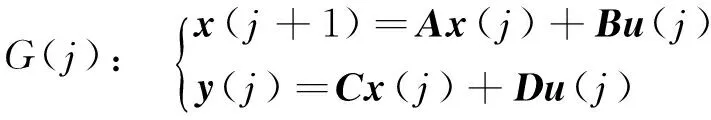
(1)
则第k次迭代时输入输出关系为:
(2)
式中:H—脉冲传递函数矩阵,H∈RN×N;uk—有限离散控制输入指令,uk=[u(0),…,u(N-1)]T;yk—有限离散系统输出信号,yk=[y(0),…,y(N-1)]T,k代表迭代次数。
若控制系统误差为:
ek=rset-yk
(3)
采用如下迭代学习算法:
uk+1(t)=Q[uk(t)+Lek(t)]
(4)
式中:Q∈n×n,L∈n×n,uk∈n,ek∈n。
基于式(4)迭代学习控制结构如图1所示。

图1 迭代学习控制框图
2 控制器的设计
2.1 稳定性和收敛性分析
假设矩阵A∈n×n,则矩阵谱半径定义为:
(5)
式中:ζi(A)—矩阵A的第i个特征值。
矩阵A最大奇异值定义为:
(6)
由式(3,4)可得出:
uk+1=Q(I-LH)uk+QLrset
(7)
根据线性系统理论及迭代学习控制系统的稳定性及渐进收敛条件可知,图1所示的迭代学习控制结构的稳定性条件为:
ρ(Q(I-LH))<1
(8)
渐近收敛条件为:
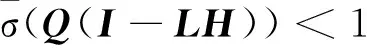
(9)
根据矩阵论知识可知,结合式(8,9)可得出:
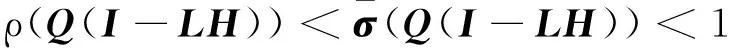
(10)
其在频域的收敛性条件也可表达为:
|1-L(ejω)H(ejω)|<|Q-1(ejω)| ∀ω
(11)
此时迭代学习控制系统是稳定且渐进收敛的。
2.2 控制器的设计
采用前馈及反馈二自由度控制结构如图2所示。
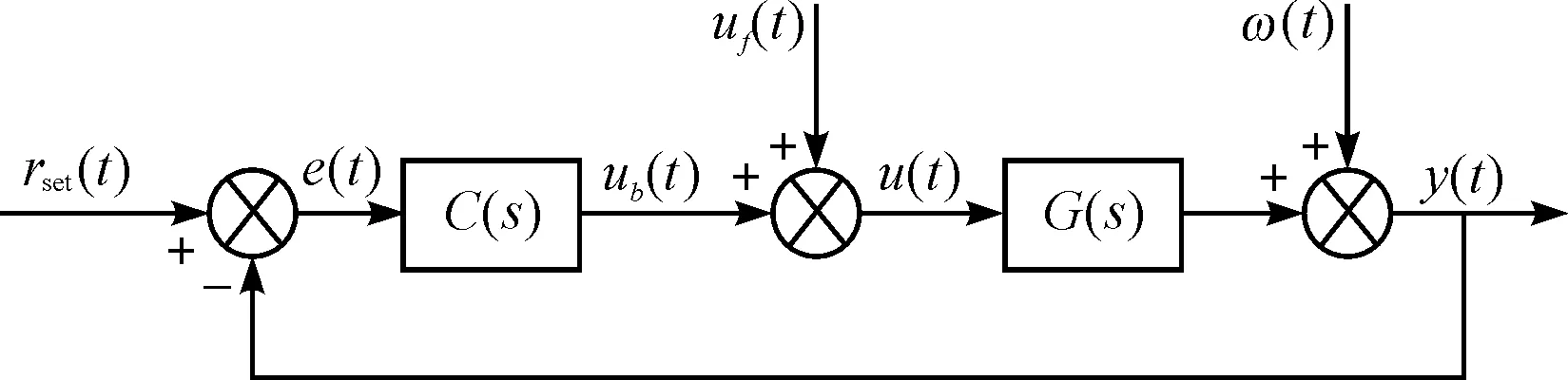
图2 二自由度控制系统结构图C(s)—反馈控制器保证系统闭环稳定;G(s)—被控对象;rset(t)—理想轨迹;e(t)—轨迹跟踪误差;ub(t)—反馈控制器输出指令;uf(t)—前馈控制指令;u(t)—被控制对象G(s)指令信号;ω(t)—扰动信号;y(t)—系统输出
本研究在反馈控制器设计稳定的基础上加入迭代学习控制算法,对前馈控制信号进行迭代修正,采用二自由度控制策略及迭代学习控制双回路控制系统结构如图3所示。
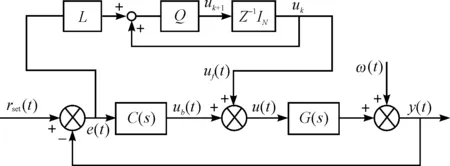
图3 迭代学习控制系统结构图
根据最优控制理论设定迭代学习控制算法的性能目标函数为:
(12)
式中:We,Wu—两个半正定加权矩阵。

(13)
经推导求得:
-HTWeek+1+Wuuk+1=0
(14)
将式(3)代入式(14),可得:
uk+1=(Wu+HTWeH)-1(HTWeH)×
(uk+(HTWeH)-1HTWeek)
(15)
结合式(4)和式(15)可得出Q,L的表达式如下所示:
(16)
令We=I,Wu=ρ·I(ρ>0),则式(16)在频域的表达式为:
(17)
式中:P(z)—输入为uf(t),输出为y(t)的系统对象模型(P(z)=G(z)/(1+C(z)G(z)))。
结合式(3)和式(14),经推导可得出:
(18)
式中:E0—未迭代前的轨迹误差。
由式(18)可知,ρ的值会对迭代学习算法收敛误差有所影响,随着ρ的增加,E∞的值逐渐增加。
3 仿真与实验
3.1 仿真分析
本研究采用Matlab/simulink对上述迭代学习控制算法进行仿真。仿真时理想轨迹采用三阶S型点到点轨迹规划进行轨迹规划,生成位移轨迹为加速度连续变化三阶位移曲线。规划参数分别为:s=0.05 m,vmax=0.2 m/s,amax=10 m/s2,jmax=3 000 m/s3验证算法性能。
轨迹规划曲线如图4所示。

图4 仿真所用三阶S型点到点轨迹
仿真对象采用通过对直线电机平台辨识的模型,如下式所示:
(19)
反馈控制器采用PID控制器构成闭环系统,其参数分别为:Kp=453 677,Ki=56 807 678,Kd=0,We=I,采用图3所示的迭代学习控制结构进行仿真,此处不考虑外界干扰对系统的影响(即默认ω(t)=0)。
加权矩阵系数ρ对迭代学习控制算法收敛速度的影响曲线如图5所示。
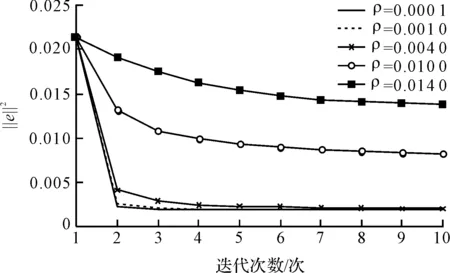
图5 ρ对收敛速度的影响曲线
从图5中可以看到:当ρ=0.001,收敛速度最快,收敛误差二范数为0.011,随着ρ的增加迭代学习算法收敛速度逐渐减小,同时迭代终值收敛逐渐增大。
ρ对迭代学习控制算法稳定性的影响曲线如图6所示。

图6 ρ对迭代学习稳定性的影响曲线
从图6中可以看到:当ρ=0.001时,|Q(1-LH)|幅值最大,其对应的稳定性范围越小,随着ρ的增加,算法的稳定性范围越大,即算法鲁棒性越强。综上分析可知,当ρ=0.000 1时,对收敛速度的影响与ρ=0.001时的结果相似,同时为了保证迭代学习算法的鲁棒性,因此,ρ的选择是算法鲁棒性与收敛速度之间的一种折衷,仿真时参数选择为We=I,Wu=10-3·I。
迭代前后误差曲线对比图如图7所示。
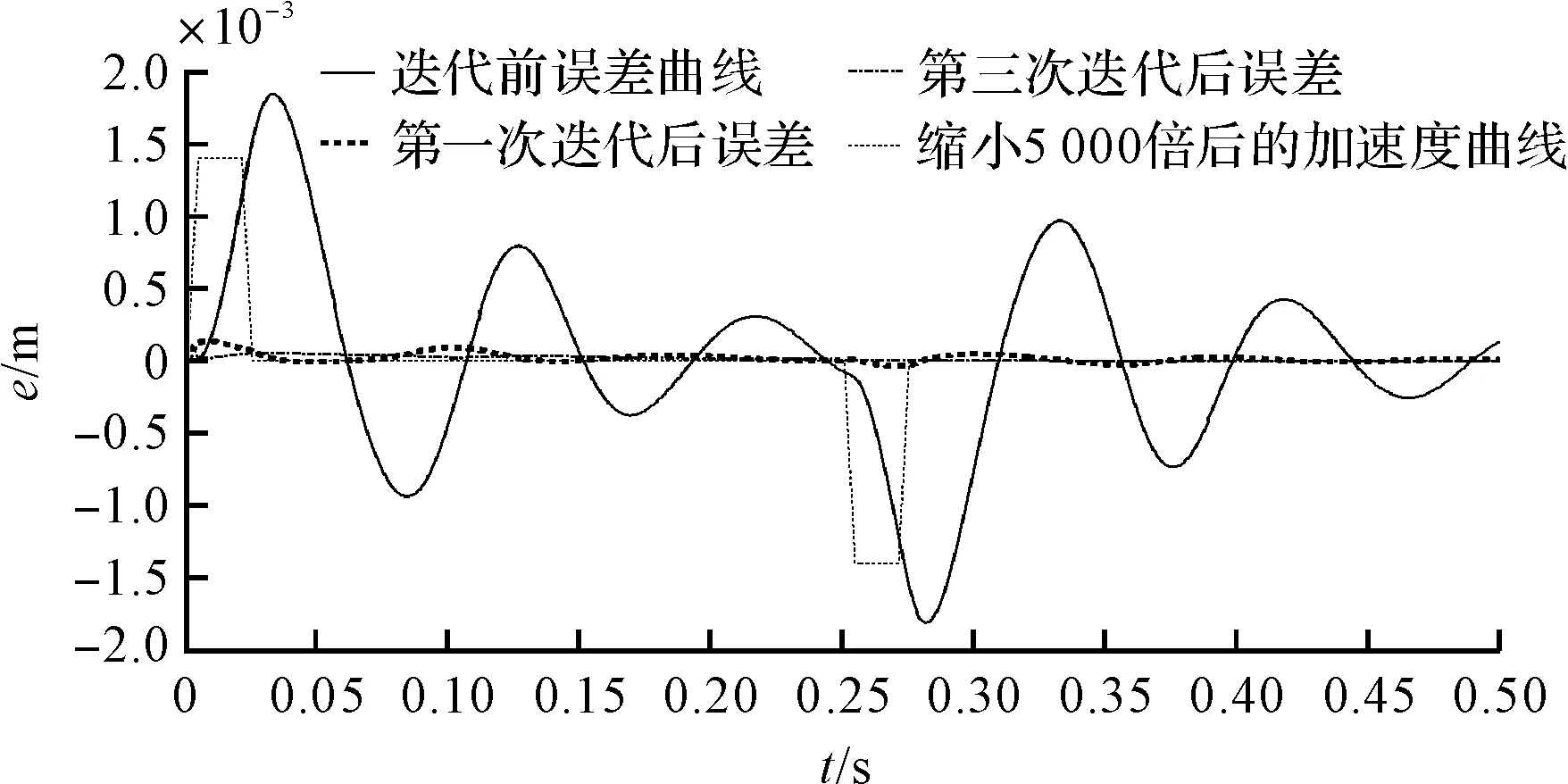
图7 迭代前后误差曲线对比图
图7中实线为未采用迭代学习控制之前的轨迹误差曲线,点线、点画线分别为第一次迭代、第三次迭代后的轨迹误差曲线(图中虚线为按一定比例缩小的加速度曲线)。从图7中可以看出:没有进行迭代时,轨迹误差数量级为10-3m,第一次、三次迭代之后误差数量级分别为10-4m和10-6m。
误差的目标函数曲线随迭代次数的变化曲线如图8所示。
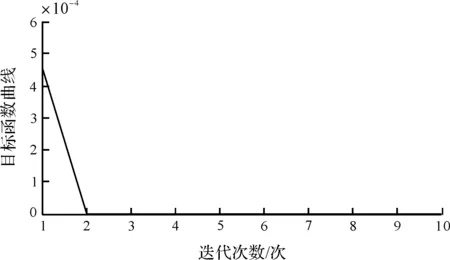
图8 迭代目标函数曲线
从图8中可以看出第二次迭代之后目标函数基本不变,与图7的结论一致,收敛效果显著。
3.2 实验验证
本文的试验平台为两个直线电动机构成的X-Y运动平台,如图9所示。

图9 直线电机实验平台
两个直线电动机均采用Baldor公司的LMCF02C-HCO,电动机的连续推力为58 N,峰值推力为173 N,直线电动机的运动位置由GSI公司分辨率为0.5 μm的光栅尺测量,读数头型号为MII1600-40。伺服驱动器为Baldor公司的FMH2A03TR-EN23,采用电流控制方式。由于位于上层直线电动机具有相对较低的惯量,为了验证高速高精性能,实际试验时采用下层直线电动机锁死,只对上层直线电动机进行试验。
实际直线伺服平台控制器与仿真结构相同,实验所采用和仿真相同三阶S型点到点轨迹。运行时间为0.5 s,伺服周期为0.000 5 s,迭代次数为10次,实验采用和仿真相同控制结构。
本文采用Matlab与C混合编程模式,利用白噪声获得闭环对象的输入输出响应,再通过Matlab系统辨识工具箱进行滤波之后经过辨识获得P(z)的ARX模型[10]:
A(z)y(t)=B(z)u(t)+e(t)
(20)
其中,
(21)
反馈控制器采用PID控制器,其参数如表1所示。

表1 控制器参数
此时令We=I,则ρ对迭代学习收敛速度的影响曲线如图10所示。

图10 ρ对收敛速度的影响曲线
图10为加权矩阵系数ρ对迭代学习控制算法收敛速度的影响曲线,从图10中可以看到:当ρ=0.001时,收敛速度最快,收敛误差二范数约为0.001,随着ρ的增加迭代学习算法收敛速度逐渐减小,同时迭代收敛误差逐渐增大。
ρ对迭代学习控制算法稳定性的影响曲线如图11所示。
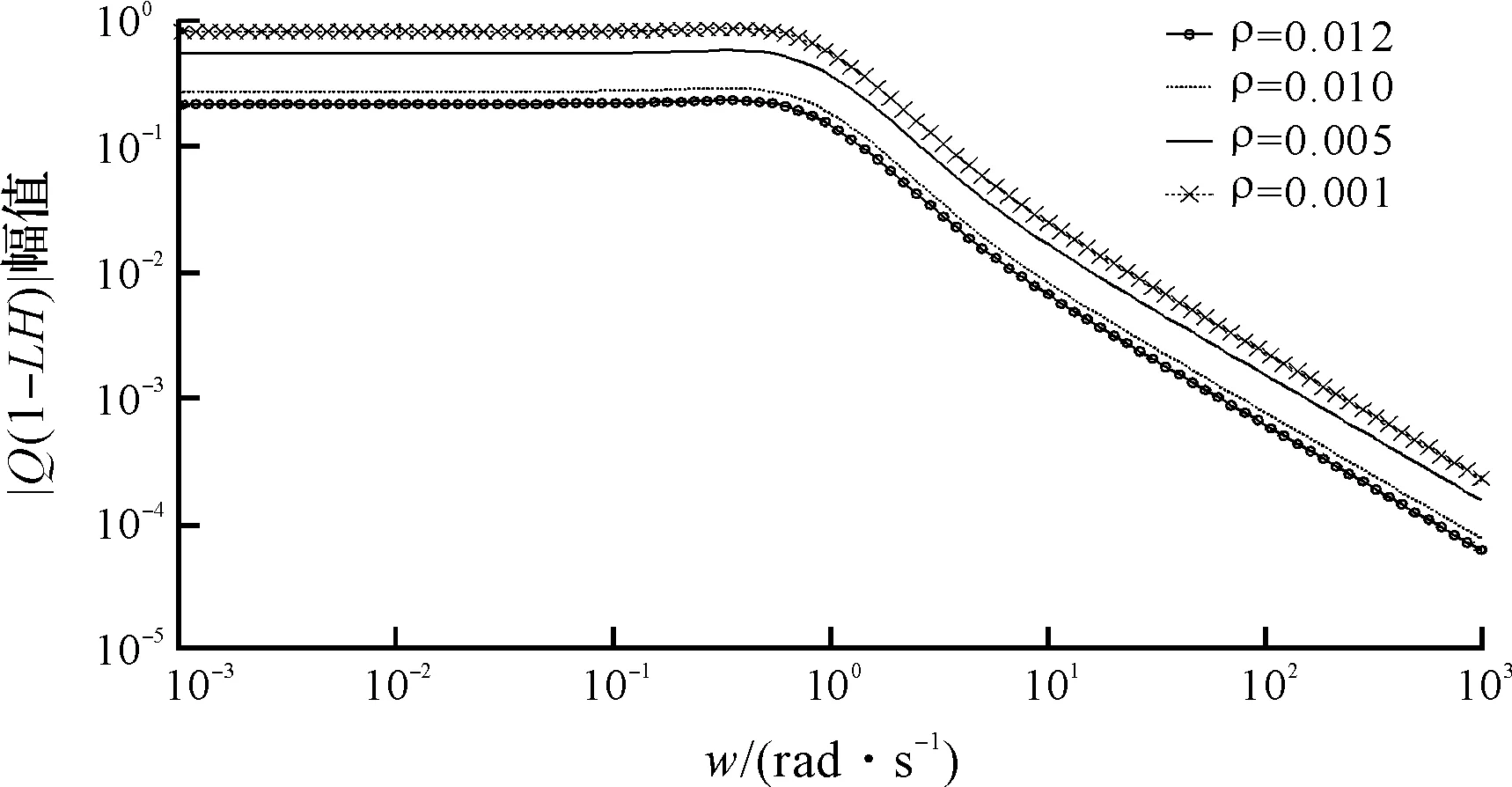
图11 ρ对迭代学习稳定性的影响曲线
从图11中可以看到:当ρ=0.001时,|Q(1-LH)|幅值最大,其对应的稳定性范围越小,随着ρ的增加,算法的稳定性范围越大,即算法鲁棒性越强。
迭代前后误差曲线对比图如图12所示。

图12 迭代前后误差曲线对比图
图12中实线为未进行迭代之前的轨迹误差曲线,点画线、虚线分别为第三次迭代、第五次迭代后的轨迹误差曲线(图中点线为按一定比例缩小的加速度曲线),在进行迭代5次之后,匀速期(即:0.05 s—0.27 s期间)误差得到了明显的收敛。
迭代目标函数曲线图如图13所示。
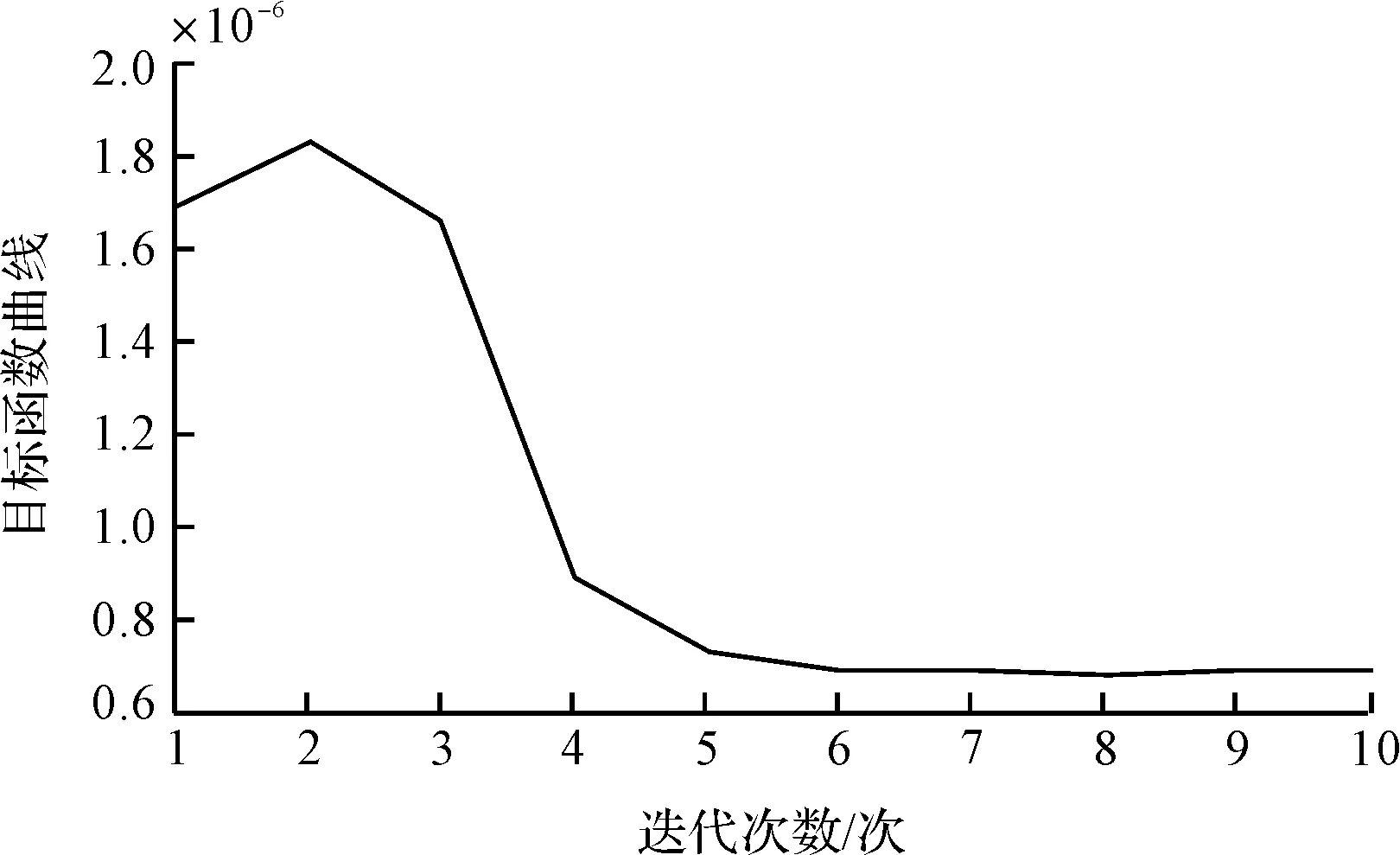
图13 迭代目标函数曲线图
从图13的目标函数曲线可以看出,误差在进行5次迭代之后基本上保持不变的趋势。由于实际直线电机平台存在一些非周期性扰动、辨识误差以及摩擦力等非线性因素的影响,误差没有完全收敛到零,但是通过实验充分验证了将本文提出的迭代学习控制算法运用到直线电机中,并且通过引入加权矩阵系数提高了算法的收敛速度。
4 结束语
基于最优控制理论,本文对迭代学习控制的收敛性进行了分析,引入加权矩阵系数,增强了算法的鲁棒性和收敛速度,并通过仿真和实际电动机平台试验,验证了本文算法的正确性;
实验结果表明:本文算法针对匀速段的收敛效果显著,提高了直线电机的运动精度。但是加减速段的收敛效果并不理想,经过对其轨迹误差频谱进行分析发现,直线电机在加减速阶段存在一个36 Hz左右的扰动信号,因此,关于加减速段的收敛效果有待进一步研究。
参考文献(References):
[1] 马 航,杨俊友,袁 琳.迭代学习控制研究现状与趋势[J].控制工程,2009,16(3):286-290.
[2] NORRLÖF M. Iterative learning control-analysis, design, and experiments[D]. Linköping: Department of Electrical Engineering, Linköpings universitet,2000.
[3] MA F, LI C. Open-closed-loop PID-type iterative learning control for linear systems with initial state error[J].JournalofVibrationandControl,2011,17(12):1791-1797.
[4] 孙明轩,毕宏博,周国良,等.反馈辅助PD型迭代学习控制:初值问题及修正策略[J].自动化学报,2015,41(1):157-164.
[5] 李 岩,陈阳泉,安孝晟.分数阶迭代学习控制的收敛性分析[J].控制理论与应用,2012,29(8):1031-1037.
[6] 刘长良,贾万根.一般非线性离散系统P-D型迭代学习收敛性研究[J].电力科学与工程,2012,28(6):69-73.
[7] 叶 腾,李传东.一类非线性时滞系统的迭代学习控制设计[J].机电工程,2010,27(2):68-70.
[8] LUO Z, WEI W, WANG J R. Robust convergence analysis of iterative learning control for impulsive Riemann-Liouville fractional-order systems[J].AdvancesinDifferenceEquations,2016(1):256.
[9] 童少伟.迭代学习型瞬时最优控制及其收敛性分析[J].力学与实践,2015,37(6):698-703.
[10] 倪博溢,萧德云.MATLAB环境下的系统辨识仿真工具箱[J].系统仿真学报,2006,18(6):1493-1496.
