直剪试验下非贯通节理岩体扩展研究

李汝嘉 齐西力 刘远明 余 洋

(1.贵州大学土木工程学院，贵州 贵阳 550025；2.贵州建设职业技术学院，贵州 贵阳 551400；3.中国地质环境监测院,北京 100081)

岩体是经受过变形、遭受过破坏的地质体,存在于一定的地质环境中，地应力、地温、地下水等因素对岩体的物理力学性质有很大影响，造成岩体内应力分布状态的复杂性[1]。节理岩体可分为贯通节理岩体和非贯通节理岩体[2-3]。节理端部应力高度集中，导致脆性断裂破坏，非贯通节理岩体整体的破坏特征表现为由原生节理和自节理端部扩展的岩桥断面所组成的复合破坏面。在非贯通节理岩体中，岩桥的贯通破坏及其变形和强度特性在很大程度上受非贯通节理面的规模、密度和空间分布特征的控制[4]。

对于节理面和岩桥研究，主要研究方法有2种：一种是实验，刘远明教授[5-8]采用带伺服系统的岩体剪切试验机，对不同起伏度的非贯通节理岩体(图1)在法向荷载为0.5、1.5、3 MPa 3种法向应力下进行直剪试验，探讨了非贯通节理岩体的贯通破坏机制，并提出了修正的非贯通节理岩体的破坏强度准则；另一种是数值模拟，使用非线性断裂力学的断裂过程区(FPZ)结合Abaqus中扩展有限元法(XEFM)研究岩石的节理扩展。将研究的结果与刘远明教授的节理扩展实验进行对比。

1 类岩石准脆性材料中裂缝的扩展与断裂过程区的关系

类岩石准脆性材料中裂缝的扩展与断裂过程区的发展紧密相关。非线性断裂力学认为在荷载作用下固体带裂缝尖端会出现一个断裂过程区(图2)，想要准确反映类岩石准脆性材料结构的裂缝抗力，就必须考虑裂缝尖端非线性区域内材料力学行为对裂缝发展的影响，通过对混凝土断裂过程区的物理解释和数学量化，可以得到各种非线性断裂模型，黏聚裂纹模型就是其中一种。在黏聚裂纹模型中，裂纹的扩展由裂尖附近裂纹面上的力—位移关系控制。黏聚裂纹模型最早由Dugdale和Barenblatt[9]提出分析金属材料,后来Hillerborg等[10]将断裂能引入黏聚裂纹模型，提出了多个力—位移关系模型。黏聚裂纹模型在准脆性材料的非线性断裂力学问题中得到了广泛的应用。

图1 非贯通节理岩体试样(单位：mm)

图2 不同材料裂缝尖端对比Fig.2 Comparison of cutting edges of different materials L—线弹性区；N—非线性区；F—断裂过程区

在裂纹扩展前，在裂纹尖端存在一个微裂区(图3)，在这个区域分布着抵抗开裂的黏聚力，黏聚力随着微裂区裂纹的张开宽度变大而逐渐减小，黏聚力为零的点就是真实裂纹的端点。Hilerbing把断裂能的概念引入黏聚力裂纹模型中，可以对岩石及混凝土等脆性材料裂纹扩展进行准确分析[11]。

图3 黏聚裂缝模型Fig.3 Cohesive fracture model

2 软化关系

对于岩石及混凝土等脆性材料裂缝扩展常用的软化关系有直线型、双线性型[12]以及幂函数型，如图4、图5所示。

除直线型外，双线性软化曲线是工程分析应用较多的混凝土软化本构模型。从双线性软化曲线看，曲线形状的确定需要4个参数：σt、σs、ωs和ω0，而抗拉强度σt一般通过拉伸或者劈裂实验测定，所以决定软化曲线形状的参数只有σs、ωs和ω0,其数学表达式为

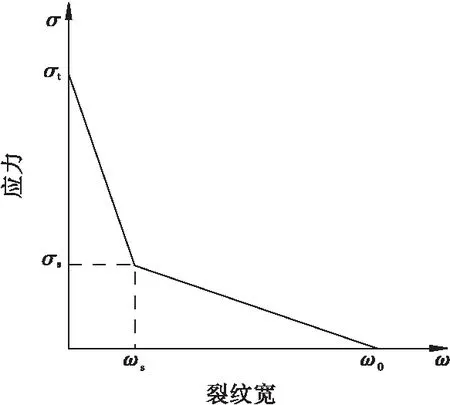
图4 双线性型Fig.4 Bilinear type

图5 幂函数型Fig.5 Power function type

(1)

对于转折点的选取关于参数σ、ωs和ω0的取值，Petersson[13]建议采用下式：

(2)

式中，Gf为岩体断裂能，N/m。

在工程应用中普遍认为岩石为准脆性材料，在混凝土试件加载到极限承载能力时，试件会经历卸载过程。通过大量的实验观察，宏观上在试件卸载的初期，承载能力急剧下降，而在后期会出现较为平缓的卸载过程，表现出一定的塑性性能，在微观中延长极限张开位移可实现岩石塑性性能。有鉴于此，提出一种优化的新型软化曲线，即将双线性软化曲线的前段与冥函数进行拟合，拟合后的的新型软化曲线如图6所示。本构关系如式(3)所示。

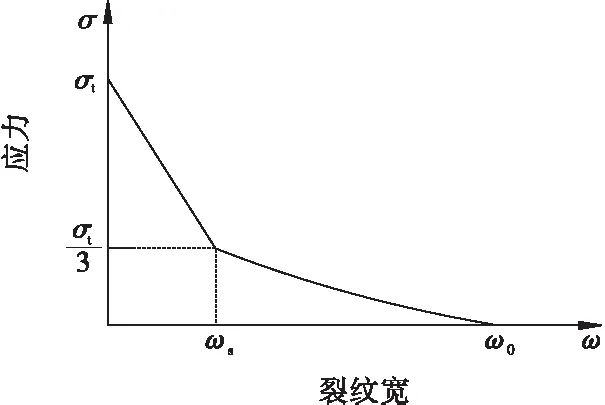
图6 优化软化曲线Fig.6 Optimize the softening curve

(3)

3 不同法向应力下非贯通节理岩体扩展贯通数值模拟

3.1 连通率0.5、起伏角0°非贯通节理岩体

节理连通率0.5、节理起伏角0°非贯通节理岩体在法向应力分别为0.5、1.5、3 MPa的数值模拟结果如图7所示,剪应力—切向位移曲线如图8所示。

图7 起伏角0°节理扩展轨迹Fig.7 Undulating angle 0° jointextended trajectory diagram

图8 起伏角0°剪切力—切向位移曲线Fig.8 Undulating angle 0° shear force-

图7中数值模拟底部设置为没有水平约束的活动支座，上部采用施加荷载，数值模拟的情况为左侧裂纹先发展且发展速度较快，这与约束条件是吻合的。

图8显示了3种不同轴压力下的剪切力—切向位移关系，数值模拟与实验结果都显示，随着轴向压力的增大，相同切向位移下的剪切应力也相应增大，这是因为随着轴压力的增大，节理面上的摩擦力也会随之正向增长，即增大了构件的整体抗剪切能力。实验与数值模拟结果在3种轴向力下的最大剪切应力的误差分别为5.56%、2.54%、-4.64%。

3.2 连通率0.5、起伏角15°非贯通节理岩体

节理起伏角15°时，在相对滑动就会存在裂缝闭合的问题，常规的扩展有限对于裂缝的闭合无法计算分析。本研究在深入分析了裂缝面上的切向应力与法向应力的基础上，引入了参数损伤性稳定黏性系数。在本文分析中，黏性系数为1时可以取得很好的数值模拟效果。

节理连通率0.5、节理起伏角15°非贯通节理岩体在法向应力分别为0.5、1.5、3 MPa时数值模拟结果如图9所示,剪应力—切向位移如曲线图10所示。

图9 起伏角15°节理扩展图Fig.9 Undulating angle 15° joint extension chart

图10 起伏角15°剪切力—切向位移曲线Fig.10 Undulating angle 15° shear force-

图10显示，虽然数值模拟使用的是位移加载方式，而实验使用的是荷载加载，但在描述加载过程时较为吻合。在轴向力分别为0.5、1.5、3 MPa，所对应的最大剪切力误差分别为-0.45%、1.03%、2.38%。

3.3 连通率0.5、起伏角30°非贯通节理岩体

节理连通率0.5、节理起伏角30°非贯通节理岩体在法向应力分别为0.5、1.5、3 MPa时数值模拟结果如图11所示，剪应力—切向位移曲线如图12所示。

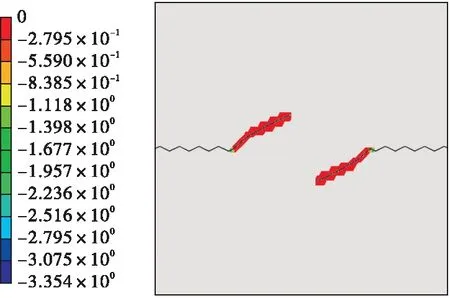
图11 起伏角30° 节理扩展图Fig.11 Undulating angle 30° joint extension chart

图12中所对应的最大剪切力误差分别为1.32%、-1.33%、-1.34% 。

通过对3种不同的轴向压力与不同起伏角度的节理扩展进行数值模拟，并对比试验结果可知，使用优化后的软化曲线模拟节理扩展具有很好的吻合性，能较为准确地反映节理的断裂行为，说明了本研究使用的优化后的软化曲线具有很好的健壮性。

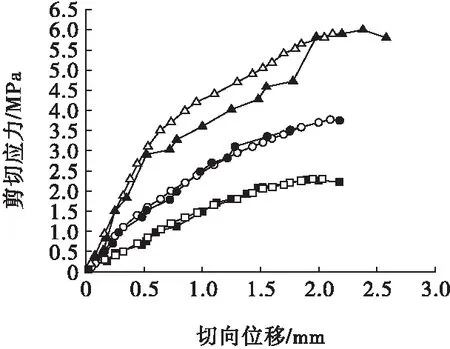
图12 起伏角30°剪切力—切向位移曲线Fig.12 Undulating angle 30° shear force-

非贯通节理岩体裂纹尖端的张拉应力达到应力极限值时，最大应力方向与起裂角度垂直，非贯通节理岩体的裂纹尖端开始产生裂纹。选取非贯通节理岩体的起裂角度为研究对象， 节理扩展的角度和法向应力的关系见图 13。图13显示，在相同的初始节理起裂角度的情况下，节理扩展的角度随着法向应力的增大而增大。节理扩展与最大法向应力是一致的，随着法向应力的增大，法向应力与节理抗力合力的角度与原节理方向的角度就越大。另一方面，在相同的法向应力的情况下，初始角度随着初始节理的角度增大而增大，原因是初始节理角度会在节理面上产生一个与法向应力相反的作用力，角度越大，这种作用力就越大，就会减小节理扩展角度与水平方向的夹角。

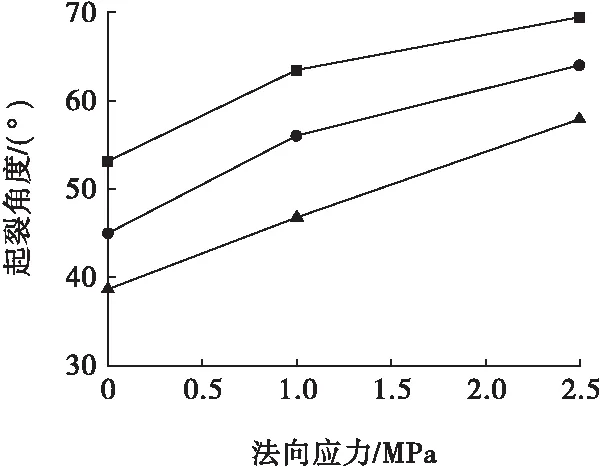
图13 不同角度下的节理扩展角度Fig.13 Angle of joint extension at different angles■—起伏度为0°;●—起伏度为15°;▲—起伏度为30°

4 讨论与结论

4.1 讨 论

(1)由于采样的局限性，实验采用的是类岩石材料，并且采用了齿型的节理表面形貌。应认识到采用试样与实际试样是有差别的。如若条件允许的情况下，采用天然的非贯通节理岩体进行研究，将提高对节理岩体的强度和变形的认知。

(2)本文使用Abaqus扩展有限元计算应力强度因子时，提出了一种新型的优化软化关系曲线，取得了一定的成果，但仍然有许多不足与有待进一步研究的问题，在今后的研究中，需进一步对这些问题进行更深层次的研究。

4.2 结 论

通过使用非线性断裂力学的断裂过程区引入断裂能可以绕开岩石节理裂纹尖端应力的奇异性，Abaqus中的XEFM模型对于岩石相似材料节理扩展的数值模拟可得出如下结果:①节理的连通率、起伏角、法向压力对非贯通岩体扩展贯通试验过程中的强度特性影响较大;②XEFM模拟的节理扩展路径与实验结果趋势是吻合的；③不同法向压力下，连通率、起伏角的非贯通节理岩体扩展数值模拟与直剪试验结果吻合较好。

[1] 李新平，朱瑞赓,朱维申，等.非贯通节理岩体的边坡稳定变形分析[J].岩石力学与工程学报,1996(3):193-200.

Li Xinping，Zhu Ruigeng，Zhu Weishen,et al.The deformation and stability of rock slope containing intermittent joints[J].Chinese Journal of Rock Mechanics and Engineering,1996(3):193-200.

[2] 蔡美峰.岩石力学与工程[M].北京：科学出版社.2004:84-89.

Cai Meifeng.Rock Mechanics and Engineering[M].Beijing:Science Press,2004:84-89.

[3] 周维垣.高等岩石力学[M].北京:水利电力出版社,1990:53-54.

Zhou Weiyuan.Advanced Rock Mechanics[M].Beijing:Water Resources and Electric Power Press,1990:53-54.

[4] 刘东燕,叶晓明,朱 凡.断续节理岩体强度评价及承载力预测[J].重庆建筑大学学报,1997,19(2):21-30.

Liu Dongyan,Ye Xiaoming,Zhu Fan.The ultimate strength evaluation of rock mass containing intermittent joints[J].Journal of Chongqing Jianzhu University,1997,19(2):21-30.

[5] 刘远明，刘 杰，夏才初.不同节理表面形貌下非贯通节理岩体强度特性直剪试验研究[J].重庆建筑大学学报,2014,35(5):1269-1274.

Liu Yuanming,Liu Jie,Xia Caichu.Research on strength behavior of rock mass containing discontinuous joints by direct shear test under different joint surface morphologies[J].Journal of Chongqing Jianzhu University,2014,35(5):1269-1274.

[6] 刘远明,夏才初.非贯通节理岩体直剪贯通模型和强度研究[J].岩土工程学报,2006,28(10):1242-1247.

Liu Yuanming,Xia Caichu.Study on models and strength behavior of rock mass containing discontinuous joints in direct shear[J].Chinese Journal of Geotechnical Engineering,2006,28(10):1242-1247.

[7] 刘远明,夏才初.非贯通节理岩体直剪试验研究进展[J].岩土力学,2007,28(8):1719-1724.

Liu Yuanming,Xia Caichu.Advances in research of rock masses containing discontinuous joints in direct shear test[J].Rock and Soil Mechanics,2007,28(8):1719-1724.

[8] 刘远明,夏才初.共面闭合非贯通节理岩体贯通机制和破坏强度准则研究[J].岩石力学与工程学报,2006,25(10):2086-2091.

Liu Yuanming,Xia Caichu.Study of fracture mechanism and criteria of failure strength of rock mass containing coplanar close discontinuous joints in direct shear[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(10):2086-2091.

[9] Theocaris P S,Gdoutos E E.The modified Dugdale-Barenblatt model adapted to various fracture configurations in metals[J].International Journal of Fracture,1974,10(4):549-564.

[10] Hillerborg Arne.Fracture Mechanics of Concrete:Nordic Seminar Held at Division of Building Materials,November 6,1986[R].Division of Building Materials,LTH,Lund University,1986.

[11] 卿龙邦,李庆斌,管俊峰,等.基于虚拟裂缝模型的混凝土断裂过程区研究[J].工程力学,2012,29(9):112-116.

Qing Longbang,Li Qingbin,Guan Junfeng,et al.Study of concrete fracture process zone based on fictitious crack model[J].Engineering Mechanics,2012,29(9):112-116.

[12] 赵志方,徐世烺.用于确定双K断裂参数的混凝土软化本构曲线[J].清华大学学报：自然科学版,2000(S1):110-113.

Zhao Zhifang,Xu Shiliang.Softening traction-separation laws of concrete for determining double-K fracture parameters[J].Journal of Tsinghua University：Science and Technology,2000(S1):110-113.

[13] Hillerborg A,Modoer M,Petersson P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J].Cement & Concrete Research,1976,6(6):773-782.