珲春曙光金铜矿地表约束对优化结果的影响分析

李金多 杨天鸿 邓文学 郑广斌 林毅斌 刘清福

(1.东北大学资源与土木工程学院，辽宁 沈阳 110819；2.珲春紫金矿业有限公司，吉林 珲春 133300)

露天矿境界优化是露天矿设计的重要环节，它既是技术决策又是经济决策，其所优化的露天矿坑形态直接影响矿山规模、投资、生产效益和服务年限，对企业生产管理和经营决策提供重要依据[1-2]。随着矿山的不断开采，矿产资源日益枯竭，如何能够可持续地发展是矿山管理者需要考虑的问题，最终目的则是在有限的信息资源和技术条件下，充分合理利用资源，减少不必要的损失，达到效益最大化[3]。在境界圈定之初为了充分利用矿物，最终开采境界应尽可能多地包含地质储量[4]。因此需要对地表约束进行详细的研究，以此确定合理的最终境界范围。从珲春曙光金铜矿2015—2016年的勘探报告中发现，原设计之初的最终境界外和开采矿权内之间仍有大量矿石。针对此问题，本研究对有地表约束和无地表约束2种条件下的境界范围变化、矿岩量变化以及价格因素对境界优化的影响变化进行分析，判断是否可以扩大地表约束范围，为珲春曙光金铜矿山生产经营者提供决策依据，并希望可以对此类的工程提供一定的借鉴意义。

1 工程概况及品位模型建立

1.1 工程概况

珲春紫金矿业有限公司曙光金铜矿(原小西南岔金铜矿)位于吉林省珲春市春化镇西15 km的山区中，是一个生产能力825万t/a的露天金铜矿。该矿山露天采场横交矿体走向布置，工作面纵向布置、横向推进，分层水平开采。采用中深孔加强松动爆破，液压挖掘机铲装，汽车运输。露天采场边坡最低点标高为470 m(位于北山矿)，最高标高为720 m(位于北山西矿)，相对高差250 m。自北山西矿帮上缘710 m平台至采区南部470 m平台，形成了20个台阶，台阶高12 m，台阶坡面角70～75°。目前北山矿采到470 m水平已进入凹陷露天开采。

1.2 品位模型建立

克里金法[5-6]是一种在一定条件下具有无偏性、最佳性等特点的线性估值方法。在合适的区域进行变量的各向异性分析，计算该区域各个主方向的半变异函数，然后以半变异函数的变程为依据确定样品搜索的影响范围。在此基础上对所获得的样品建立克里金方程组，求解并进行品位估值。

根据矿山实际生产现状及地质勘探数据所获得的估值参数如表1所示。

表1 克里金估值参数Table 1 Kriging evaluation parameters

结合Surpac软件，建立如图1所示的原矿床块体模型。模型范围：东西长2 100 m，南北宽1 200 m，高552 m。根据矿体的勘探网度和采矿台阶高度，确定地质模型的主模块尺寸在x、y、z方向上尺寸分别为12 m×12 m×12 m，主模块数约为80.5万个。图2是矿体模型，图中黑色为高品位矿，灰色为较低品位矿。

2 L-G图论法

L-G图论法是Lerchs和Grossmann于1965年提出的、具有严格数学逻辑的最终境界优化方法，只要确定了价值模型，则可以求出总价值最大最终开采境界[7]。

图1 矿床模型示意Fig.1 Deposit block model

图2 矿体模型示意Fig.2 Ore body model

L-G图论法优化基础是以最终边坡角为几何约束将赋予价值属性的矿体块体模型构成有向图G。其中价值模型中的模块对应图中的节点，模块中的净价值数值对应图中的权值。把满足几何约束条件的开采境界称为图的闭包，闭包中的权值等于闭包内各个节点权值之和，有向图G中权值最大的闭包称为最大闭包。而从实际采矿的角度来看，最大闭包是具有最大开采价值的开采境界，因此求最佳境界就是求价值模型所对应图中的最大闭包。

图论法方块模型与图和子集如图3所示，其中图3(a)是由6个大小相等的正方形模块组成的价值模型，xi(i=1，2，…，6)表示第i块的位置，wi表示第i块模型的权值，最终边坡角设为45°，那么该模型图论法表示为图3(b)，而图3(c)、3(d)是图3(b)的子图。图3(b)、3(c)、3(d)都为可行闭包且Vb为图3(b)闭包的权值，Vc为图3(c)闭包的权值，Vd为图3(d)闭包的权值，通过比较这3个闭包的权值，得出最大闭包。

图3 图论法方块模型与图和子集Fig.3 Box model，graph and subsetbased on graph theory

3 境界优化与分析

珲春紫金曙光金铜矿于2015—2016年间在原设计境界内补勘大量地质钻孔，紫金矿业集团股份有限公司矿产地质勘查院基于原钻孔资料和补录的资料重新建立地质品位模型，核算矿山当前保有储量。结果表明，原设计境界北部部分超出林地及地表矿权约束界限，南部和东部采矿权内露天开采境界外仍有大量矿石，如图4所示。因此针对此情况重新进行境界优化，并对有地表约束优化和无地表约束优化境界2种情况作出对比分析。

图4 地表约束线与原设计境界线(单位：m)

3.1 境界优化

本次采用Whittle软件作为境界优化软件。该软件首先根据参数化调整法生成一系列境界，然后根据各种限制条件和排产目标进行人工或数学模型自动优化排产，根据生产规划结果计算系列境界的NPV，最后通过方案比较确定最优开采顺序和最终境界[8-10]。

在境界优化中参数选择对于优化结果非常重要。本次境界优化中所选用参数均来自矿山实际生产数据。表2是境界优化经济参数表，图5是各分区边坡角度。本次境界优化主要分为两种情况进行：一是以图4中紫色林地及地表矿权约束线(以下简称约束线)为约束条件进行境界优化；二是无地表约束进行境界优化。优化结果如表3，表中边界品位为已将铜矿石考虑在内的金金属量的折合品位；优化后的境界三维图如图6所示。

表2 境界优化经济参数Table 2 Economic parameters of the boundary optimization

图5 不同分区边坡角度数Fig.5 Slope angle of different regions表3 境界优化结果Table 3 Results of boundary optimization

条 件边界品位/(g/t)利 润/万元矿石合计/万t岩石合计/万t矿岩合计/万t剥采比/(t/t)开采年限/a有约束0.38279288.079088.175099.7714188.940.5611.02无约束0.38307633.4811955.307834.9319790.230.6614.49

由表3可以看出由于境界线的约束使得有地表约束境界比无地表约束境界少开采约2 867万t矿石，少剥离约2 737万t岩石。经济损失约28 345万元。

图6 境界优化三维图Fig.6 Three-dimensional graph underboundary optimization

为了更清晰地表述2种条件下的境界线对比，我们将2种条件下的境界线按照边坡角区域划分为6块区域，如图7所示，图中紫线为约束线，黑线为无约束条件下的境界优化线，红色为有约束条件下的境界优化线。

从图7中我们可以看出在II区和III区中2种条件下的境界线重合且都未超出约束线，说明这2块区域约束影响不大；在Ⅰ区、Ⅳ区、Ⅴ区和Ⅵ区中无约束条件下境界线均超出约束线，且2种条件下的境界线相差为：Ⅰ区外扩150 m，Ⅳ区外扩340 m，Ⅴ区外扩70 m，Ⅵ区上部外扩108 m，说明Ⅰ、Ⅴ、Ⅵ 3块区域约束影响较大，而Ⅳ区域约束影响最大。

图7 各区域境界范围图(单位:m)

3.2 价格发生改变对境界优化的影响

在保证其他技术经济参数不变条件下，通过改变精矿的价格系数来分析价格变化对有约束和无约束条件下的境界优化影响，其中当前价格条件下的价格系数为1。优化结果如表4和表5所示,同表3，边界品位为金铜矿石的折合品位。

表4 有约束条件下境界优化表Table 4 Boundary optimization with surface restriction

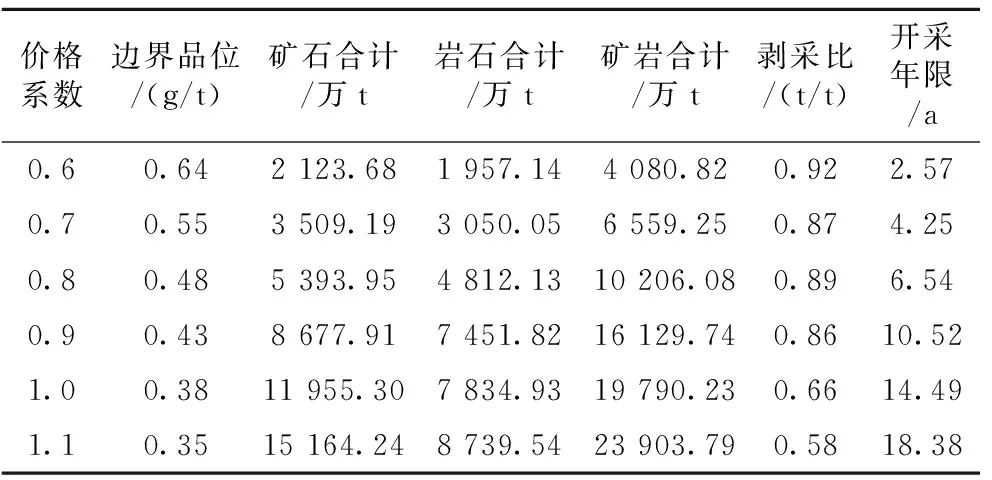
表5 无约束条件下境界优化表Table 5 Boundary optimization with on surface restriction

从表4和表5可以看出，当价格系数为1.1时有约束条件下矿量增加18%，无约束条件下矿量增加27%；当价格系数为0.9时有约束条件下矿量减少20%，无约束条件下矿量减少27%。由此我们知道有约束条件和无约束2种条件下的境界对价格的灵敏度都较高。同时我们可以看出当价格系数为0.6时，无约束条件境界矿量比有约束条件境界矿量多0.7%；当价格系数为0.8时，无约束条件境界矿量比有约束条件境界矿量多5%；当价格系数为0.9时，无约束条件境界矿量比有约束条件境界矿量多16%；当价格系数为1时，无约束条件境界矿量比有约束条件境界矿量多31%；当价格系数为1.1时，无约束条件境界矿量比有约束条件境界矿量多41%。因此当价格系数为0.8及以下时，地表约束对境界的影响不大，而当价格系数大于0.8时，地表约束对于境界的影响明显提升。图8表示部分不同价格系数条件下有无约束条件的境界变化。

图8 2种不同价格系数条件下的境界示意Fig.8 Boundary diagram of two conditionsunder different price

3.3 有无约束线各区域矿岩量分析

在3.1节中讲到为了更好地分析比较2种条件下的境界优化结果，把矿区分成了6个区域，如图5所示。表6是2种条件下各区域的矿岩变化。

表6 2种条件各区域矿岩变化Table 6 Variation of ore and rock in different regionsunder two conditions ×104 t

由表6可以看出由于境界线的约束使得在当前价格条件下2种境界内约相差矿石2 867万t、岩石2 737万t。其中地表约束对Ⅳ区矿岩量影响最大，矿石占总增量的64.6%，岩石占总增量的70.9%；对Ⅰ、Ⅴ、Ⅵ区矿岩量影响较大，矿石占总增量分别为12.3%、12.4%、10.5%，岩石占总增量分别为11.5%、11.3%、6.15%；而对Ⅱ、Ⅲ区矿岩量基本无影响。

把Ⅳ区域作为主要研究对象，按年生产能力825万t/a计算，需要开采2.3 a。可产生利润2亿元，假设未来3 a内精矿价格和成本均不发生变化，以折现率10%进行折算，这相当于现值1.6亿元。若获取Ⅳ区所需矿权费用、征林费用及其他相关费用小于1.6亿元则可进行开采。

4 结 论

(1)基于矿山提供的技术经济参数以及目前精矿市场价格，有地表约束境界比无地表约束境界少采2 867万t，其中影响最大的为Ⅳ区。

(2)有约束和无约束2种条件下的境界对价格的灵敏度都较高，且当价格系数在0.8及以下，境界基本不受地表约束影响，而在0.8以上，境界受地表约束影响显著提升。

(3)未来3 a成本不变的情况下，若矿权费用、征林费用及其他相关费用小于1.6亿元时，即可对Ⅳ区进行开采。

[1] 王 青，任凤玉．采矿学[M]．北京：冶金工业出版社，2011．

Wang Qing，Ren Fengyu．Mining Science[M]．Beijing：Metallurgical Industry Press，2011．

[2] 张延凯，胡乃联，徐国伟，等．某铜钼矿开采境界优化研究[J]．中国矿业，2012，21(10)：84-87．

Zhang Yankai，Hu Nailian，Xu Guowei，et al．Pit optimization for one copper-molybdenum mine[J]．China Mining Magazine，2012，21(10)：84-87．

[3] 朱维根．矿产资源开发与可持续发展[J]．中国矿业，2004，13(9)：44-46．

Zhu Weigen．Mining resouce and the sustainable development[J]．China Mining Magazine，2004，13(9)：44-46．

[4] 王海军，王 青，顾晓薇，等．露天矿最终境界的优化研究[J]．矿冶，2011，20(4)：33-37．

Wai Haijun，Wang Qing，Gu Xiaowei，et al．Study on optimization of final boundary of open pit mine[J]．Mining & Metallurgy，2011，20(4)：33-37．

[5] 陈小文，宋革文．克立格估值法在SURPAC块体建模中的应用[J]．金属矿山，2009(10)：137-139．

Chen Xiaowen，Song Gewen．Application of Kriging estimation method in SURPAC block model[J]．Metal Mine，2009(10)：137-139．

[6] 滕正双，于洪苹．基于3DMine软件的地质统计学在河北羊崖山铁矿床资源量估算中的应用[J]．地质找矿论丛，2015，30(3)：374-382．

Teng Zhengshuang，Yu Hongping．Application of geological statistics based on 3DMine software to estimate the resources of Yangyashan iron deposit in Hebei province[J]．Contributions to Geology and Mineral Resources Research，2015，30(3)：374-382．

[7] Lerchs H，Grossman I．Optimum design of open-pit mines[J] .Transactions，Canadian Institute of Mining，1965，68(1)：17-24．

[8] 杨 彪．Whittle在露天矿开采境界优化中的应用[J]．有色金属：矿山部分，2013，65(3)：24-28．

Yang Biao．Application of Whittle in open pit mining limit optimization[J]．Nonferrous Metals：Mining Section，2013，65(3)：24-28．

[9] Shaman P．Properties of generalized Levinson-Durbin-Whittle sequences[J]．Journal of Statistical Planning & Inference，2008，138(9)：2808-2814．

[10] Guo H，Lim C Y，Meerschaert M M．Local Whittle estimator for anisotropic random fields[J]．Journal of Multivariate Analysis，2009，100(5)：993-1028．